Выпускная квалификационная работа теория графов
 Скачать 0.56 Mb. Скачать 0.56 Mb.
|
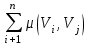 - вес маршрута. W = (wij) - матрица весов, (wij)= μ(Vi, Vj), если Vi, Vj€ U; (wij)=00, если (Vi, Vj ) - вес маршрута. W = (wij) - матрица весов, (wij)= μ(Vi, Vj), если Vi, Vj€ U; (wij)=00, если (Vi, Vj ) 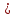 U U Предположим, что в G отсутствуют контуры с отрицательным весом, поскольку, двигаясь по такому контуру достаточное количество раз, можно получить маршрут, имеющий вес, меньший любого заведомо взятого числа, и тем самым задача нахождения расстояния становиться бессмысленной. Определим алгоритм Форда-Белмиана.  Зададим строку 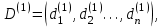 полагая полагая 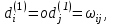 В этой строке В этой строке 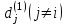 есть вес есть вес 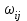 дуги дуги 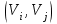 , если , если 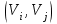 существует, и существует, и 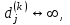 если если 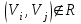 Определим строку 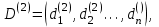 полагая dj(2) = min {dj(1), dk(1) + ωkj}k=1,…n полагая dj(2) = min {dj(1), dk(1) + ωkj}k=1,…nНетрудно заметить, что dj(2) - минимальный из весов (Vi, Vj) - маршрутов, состоящий не более, чем из двух дуг (рис. 35). Продолжая процесс, на шаге S определим строку Д(s) = (d1(s), d2(s),…, dn(s)), полагая dj(s)= min { dj(s-1), dk(s-1) + ωkj}k=1,…n Искомая строка ω-расстояний получается при s = n - 1 : dj(n-1)= ρω (Vi, Vj). Действительно, на этом шаге из всех весов (Vi, Vj) -маршрутов, содержащих не более (n-1) дуг, выбирается наименьший, а каждый маршрут более чем с (n-1) дугами содержит контур, добавление которого к маршруту не уменьшает ω-расстояния, т.к. было предположение отсутствия контуров отрицательного веса. Работу алгоритма можно завершить на шаге к, если Д(к) = Д(к+1). Пример: Продемонстрируем работу алгоритма Форда-Беллмана. На примере взвешенного графа, показанного на рис.36 с матрицей весов.  В качестве источника выберем Т - {1}, тогда Д(1) = (0, 1, ∞ , ∞, 3), min маршрут сост. 1 дуги Д(2) = (0, 1, 4, 4, 3), не более 2 дуг Д(3) = (0, 1, 4, 4, -1), 3 дуг Д(4) = (0, 1, 4, 3, -1). 4 дуг Таким образом, ρω (1, 1) = 0, ρω (1, 2) = 1, ρω (1, 3) = 4, ρω (1, 4) = 3, ρω (1, 5) = -1. Зная расстояние от источника Vi до всех остальных вершин графа, можно найти и сами кратчайшие (Vi, Vj) -маршруты. Действительно, пусть Vi, b1, b2, …, br, Vj - кратчайший (Vi, Vj) -маршрут. Тогда по строке Д(n-1) вершина br = Vk2 находится из соотношения ρω (Vi, Vj) = ρω (Vi, Vк1) + ωк1j, вершина br-1 = Vк2 из ρω (Vi, Vк1) = ρω (Vi, Vк2) + ωк2к1 и т.д. В предыдущем примере кратчайший (1, 4)-маршрут определяется следующим образом: ρω (1, 4) = 3 = -1 + 4 = ρω (1, 5) + ω54, тогда br = 5; ρω (1, 5) = -1 = 4 - 5 = ρω (1, 3) + ω3,5, откуда br-2 = b2 = 3, br-3 = b1 = 2. Таким образом, кратчайший (1,4)-маршрут задается последовательностью вершин (1, 2, 3, 5, 4). Алгоритм Дейкстры является более эффективным, чем алгоритм Форда-Беллмана, но используется только для взвешенных графов, в которых веса всех дуг неотрицательны.  Алгоритм Дейкстры: -источник Т1 = {2, 3, 4, 5, 6} Д(1) = {0, 1, ∞, ∞, ∞, ∞} -источник Т2 = {3, 4, 5, 6} Д(2) = {0, 1, 6, 3, ∞, ∞} Д(1) = {d1(1), d2(1), d3(1), d4(1), d5(1), d6(1)} d1(1) = 0, dj(1) = ωij. Д(2) = {d1(2), d2(2), d3(2), d4(2), d5(2), d6(2)} dj(2) = min {dj(1), dk(1) + ωkj}, k = 1, 2, …, n d2(2) = min {d2(1), dk(1) + ωk2} = min {1, 0 + 1} = 1 d3(2) = min {d3(1), dk(1) + ωk3} = min {∞, 1 +5} = 6 d4(2) = min {d4(1), d2(1) + ω24} = min {∞, 1 + 2} = 3 d5(2) = min {∞, d6(1) + ω65} = {∞, ∞} = ∞ d6(2) = min {∞, ∞ + ω36} = ∞ _______________________________ Д(3) = {d1(3), d2(3), d3(3), d4(3), d5(3), d6(3)} T3 = {3, 5, 6} 4 - источник Д(3) = {0, 1, 4, 3, 7, 8} d3(3) = min {d3(2), d4(2) + ω43} = min {6, 3 + 1} = min {6, 4} = 4 d4(3) = min {3, d2(2) + ω24} = min {3, 1 + 2} = 3 d5(3) = min {∞, d6(2) + ω65} = {∞, d4(2) + ω45} = min {∞, 3 + 4} = 7 d6(3) = min {∞, d2(2) + ω36} = min {∞, 1 + 7} = 8 Д(4) = {d1(4), d2(4), d3(4), d4(4), d5(4), d6(4)} T4 = {5, 6} Д(4) = {0, 1, 4, 3, 7, 5} d4(4) = min {d4(3), d2(3) + ω23} = min {3, 1 + 5} = 3 d5(4) = min {d5(3), d6(3) + ω65} = 3 d6(4) = min {d6(3), d3(3) + ω36} = min {8, 4 + 1} = 5 T5 = {5} Д(5) = {d1(5), d2(5), d3(5), d4(5), d5(5), d6(5)} Д(5) = {0, 1, 4, 3, 6, 5} d4(5) = min {d4(4), d2(4) + ω24} = min {3, 1 + 2} = 3 d5(5) = min {d5(4), d6(4) + ω65} = min {7, 5 + 1} = 6 d6(5) = min {d6(4), d3(4) + ω36} = min {5, 4 + 1} = 5 ρω (1, 1) = 0 ρω (1, 2) = 1 ρω (1, 3) = 4 ρω (1, 4) = 3 ρω (1, 5) = 6 ρω (1, 6) = 5 Минимальный путь из V1 до V7 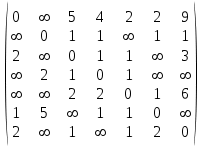 -источник Т1 = {2, 3, 4, 5, 6, 7} Д(1) = {0, ∞, 5, 4, 2, 2, 9} -источник Т2 = {2, 3, 4, 6, 7} Д(2) = {0, ∞, 4, 4, 2, 2, 8} d2(2) = min {d2(1), d5(1) + ω52} = min {∞, 2 + ∞} = ∞ d3(2) = min {d3(1), d5(1) + ω53} = min {5, 2 +2} = 4 d4(2) = min {d4(1), d5(1) + ω54} = min {4, 2 + 2} = 4 d5(2) = min {d5(1), d5(1) + ω56} = min {2, 2 + 0} = 2 d6(2) = min { d6(1), d5(1) + ω56} = min {2, 2 + 1} = 2 d7(2) = min { d7(1), d5(1) + ω57} = min {9, 2 + 6} = 8 -источник Т3 = {2, 3, 4, 7} Д(3) = {0, 7, 4, 3, 2, 2, 8} d2(3) = min {d2(2), d6(2) + ω62} = min {∞, 2 + 5} = 7 d3(3) = min {d3(2), d6(2) + ω63} = min {4, 2 + ∞} = 4 d4(3) = min {d4(2), d6(2) + ω64} = min {4, 2 + 1} = 3 d5(3) = min {d5(2), d6(2) + ω65} = min {2, 2 + 1} = 2 d6(3) = min {d6(2), d6(2) + ω66} = min {2, 2 + 0} = 2 d7(3) = min {d7(2), d6(2) + ω67} = min {8, 2 + ∞} = 8 -источник Т4 = {2, 3, 7} Д(4) = {0, 5, 4, 3, 2, 2, 8} d2(4) = min {d2(3), d4(3) + ω42} = min {7, 3 + 2} = 5 d3(4) = min {d3(3), d4(3) + ω43} = min {4, 3 + 1} = 4 d4(4) = min {d4(3), d4(3) + ω44} = min {3, 3 + 0} = 3 d5(4) = min {d5(3), d4(3) + ω45} = min {2, 3 + 1} = 2 d6(4) = min {d6(3), d4(3) + ω46} = min {2, 3 + ∞} = 2 d7(4) = min {d7(3), d4(3) + ω47} = min {8, 3 + ∞} = 8 -источник Т5 = {2, 7} Д(5) = {0, 5, 4, 3, 2, 2, 7} d2(5) = min {d2(4), d3(4) + ω32} = min {5, 4 + ∞} = 5 d3(5) = min {d3(4), d3(4) + ω33} = min {4, 4 + 0} = 4 d4(5) = min {d4(4), d3(4) + ω34} = min {3, 4 + 1} = 3 d5(5) = min {d5(4), d3(4) + ω35} = min {2, 4 + 1} = 2 d6(5) = min {d6(4), d3(4) + ω36} = min {2, 4 + 1} = 2 d7(5) = min {d7(4), d3(4) + ω37} = min {8, 4 + 3} = 7 -источник Т6 = {7} Д(6) = {0, 5, 4, 3, 2, 2, 6} d2(6) = min {d2(5), d2(5) + ω22} = min {5, 5 + 0} = 5 d3(6) = min {d3(5), d2(5) + ω23} = min {4, 5 + 1} = 4 d4(6) = min {d4(5), d2(5) + ω24} = min {3, 5 + 1} = 3 d5(6) = min {d5(5), d2(5) + ω25} = min {2, 5 + ∞} = 2 d6(6) = min {d6(5), d2(5) + ω26} = min {2, 5 + 1} = 2 d7(6) = min {d7(5), d2(5) + ω27} = min {7, 5 + 1} = 6 ρω (1, 1) = 0 ρω (1, 2) = 5 ρω (1, 3) = 4 ρω (1, 4) = 3 ρω (1, 5) = 2 ρω (1, 6) = 2 ρω (1, 7) = 6 § 4. Раскраска графов Пусть G = <V, U> - нефграф без петель. Раскраской (вершин) графа G называется такое задание цветов вершинам G, что если (Vi, Vj)-дуга, то вершины Vi, Vj имеют различные цвета. Хроматическим числом Х (G) графа G называется минимальное число цветов, требующиеся для раскраски G (рис. ) Пример. Так как в полном графе Gn любые две различные вершины связаны ребром, то Х (Gn) = n. Многие практические задачи сводятся к построению раскрасок графов. Пример 1. Рассмотрим задачу составления расписания. Предположим, что нужно прочесть несколько лекций за кратчайшее время. Чтение каждой лекции в отдельности занимает один час, но некоторые лекции не могут читаться одновременно. Построим граф G, вершины которого биективно соответствуют лекциям и две вершины смежны тогда и только тогда, когда соответствующие им лекции нельзя читать одновременно. Очевидно, что любая раскраска этого графа определяет допустимое расписание: лекции, соответствующие вершинам одного цвета, могут читаться одновременно. Напротив, любое допустимое расписание определяет раскраску графа G. Оптимальные расписания соответствуют раскраскам с минимальным числом цветов, а число часов, необходимое для прочтения всех лекций, равно Х (G). Пример 2. Рассмотрим граф G, вершины которого - страны, а ребра соединяют страны, имеющие общую границу. Число Х (G) соответствует наименьшее число красок, необходимых для раскраски карты так, чтобы никакие две соседние страны не были окрашены в один цвет. Пример. Проводится монтаж аппаратуры. Чтобы не перепутать проводники, необходимо их окрасить таким образом, чтобы два проводника, идущие к одной плате, имели разные цвета. В этом случае вершинами являются платы, а ребрами - проводники. Неорграф G называется бихроматическим, если Х (G) = 2. Неорграф G = <V, U> называется двудольным, если множество всех ребер графа G образует разрез графа G, т.е. для некоторого разбиения множества вершин {V1, V2} концы любого ребра принадлежат разным частям разбиения. Примером служит задача «Три дома, три колодца». Рассмотрим простой алгоритм построения раскраски, который во многих случаях приводит к раскраскам, близким к минимальным. . Произвольная вершина V1 графа G принимает цвет 1. . Если вершины V1, …, Vi раскрашены l цветами е, 2, … е, е ≤ i, то новой произвольно взятой вершине Vi+1 припишем минимальный цвет, не использованный при раскраске вершин из множества {Vj | ρ (Vi+1, Vj) = 1, j < i}. Для некоторых классов графов последовательная раскраска является минимальной. В общем случае это не так. Все двудольные графы бихроматические, Х (G) = 2. Пример: бихроматический двудольный Любой бихроматический граф является двудольным. Теорема: для того, чтобы граф был бихроматическим, необходимо и достаточно, чтобы он был связным и не содержал элементарных циклов нечетной длины. Дано: G - бихромат. граф Док-ть: связный и не содержит циклов нечетной длины Док-во (от противного) Пусть граф содержит циклический элемент Х = 3, но G - бихромат - противоречие. Обратная теорема: Дано: G - связный, не содержит циклов нечет. длины Док-ть: Х (G) = 2 Док-во: ) рассм. связный граф, который не имеет циклов ) граф, содержит циклы четной длины § 5. Эйлеровы и гамильтоновы графы Как указано в предисловии, задача о Кенигсбергских мостах послужила началом математической теории графов. План расположения семи мостов в Кенигсберге приведен на рис.39. |
