Задачи для тренировки

Название	Задачи для тренировки
Дата	16.03.2023
Размер	375.5 Kb.
Формат файла
Имя файла	ege9.doc
Тип	Документы #994423
страница	3 из 3

1 2 3

А. Богданов). Откройте файл электронной таблицы 9-107.xls, содержащей в каждой строке три натуральных числа. Выясните, какое количество троек чисел могут являться величинами углов треугольника, выраженных в градусах. В ответе запишите только число.

(А. Богданов). Откройте файл электронной таблицы 9-107.xls, содержащей в каждой строке три натуральных числа. Выясните, какое количество троек чисел не могут являться величинами углов треугольника, выраженных в градусах. В ответе запишите только число.

(А. Богданов). Откройте файл электронной таблицы 9-107.xls, содержащей в каждой строке три натуральных числа. Выясните, какое количество троек чисел могут являться величинами углов остроугольного треугольника, выраженных в градусах. В ответе запишите только число.

(А. Богданов). Откройте файл электронной таблицы 9-107.xls, содержащей в каждой строке три натуральных числа. Выясните, какое количество троек чисел могут являться величинами углов тупоугольного треугольника, выраженных в градусах. В ответе запишите только число.

(А. Богданов). Откройте файл электронной таблицы 9-107.xls, содержащей в каждой строке три натуральных числа. Выясните, какое количество троек чисел могут являться величинами углов прямоугольного треугольника, выраженных в градусах. В ответе запишите только число.

(А. Богданов). Откройте файл электронной таблицы 9-107.xls, содержащей в каждой строке три натуральных числа. Выясните, какое количество троек чисел могут являться величинами углов равнобедренного треугольника, выраженных в градусах. В ответе запишите только число.

(А. Богданов). Откройте файл электронной таблицы 9-107.xls, содержащей в каждой строке три натуральных числа. Выясните, какое количество троек чисел могут являться величинами углов равностороннего треугольника, выраженных в градусах. В ответе запишите только число.

(А. Богданов). Откройте файл электронной таблицы 9-114.xls, содержащей в каждой строке три натуральных числа. Выясните, какое количество троек чисел могут являться сторонами прямоугольного треугольника. В ответе запишите только число.

(А. Богданов). Откройте файл электронной таблицы 9-114.xls, содержащей в каждой строке три натуральных числа. Выясните, какое количество троек чисел могут являться сторонами остроугольного треугольника. В ответе запишите только число.

(А. Богданов). Откройте файл электронной таблицы 9-114.xls, содержащей в каждой строке три натуральных числа. Выясните, какое количество троек чисел могут являться сторонами тупоугольного треугольника. В ответе запишите только число.

(А. Богданов). Откройте файл электронной таблицы 9-114.xls, содержащей в каждой строке три натуральных числа. Выясните, какое количество троек чисел могут являться сторонами равнобедренного треугольника. В ответе запишите только число.

(А. Богданов). Откройте файл электронной таблицы 9-114.xls, содержащей в каждой строке три натуральных числа. Выясните, какое количество троек чисел могут являться сторонами равностороннего треугольника. В ответе запишите только число.

(А. Богданов). Откройте файл электронной таблицы 9-119.xls, содержащей в каждой строке четыре натуральных числа, являющиеся последовательностью длин отрезков ломаной. Выясните, какое количество четверок чисел может являться сторонами четырехугольника. В ответе запишите только число.

(А. Богданов). Откройте файл электронной таблицы 9-119.xls, содержащей в каждой строке четыре натуральных числа, являющиеся последовательностью длин отрезков ломаной. Выясните, какое количество четверок чисел может являться сторонами описанного четырехугольника. В ответе запишите только число.

(А. Богданов). Откройте файл электронной таблицы 9-119.xls, содержащей в каждой строке четыре натуральных числа, являющиеся последовательностью длин отрезков ломаной. Выясните, какое количество четверок чисел может являться сторонами параллелограмма. В ответе запишите только число.

(А. Богданов). Откройте файл электронной таблицы 9-119.xls, содержащей в каждой строке четыре натуральных числа, являющиеся последовательностью длин отрезков ломаной. Выясните, какое количество четверок чисел может являться сторонами ромба. В ответе запишите только число.

(А. Богданов). Откройте файл электронной таблицы 9-123.xls, содержащей в каждой строке четыре натуральных числа. Выясните, какое количество четверок чисел может являться последовательностью углов (в градусах) трапеции, но не параллелограмма. Последовательность углов начинается с произвольной вершины и далее по кругу. В ответе запишите только число. Замечание: основания трапеции могут располагаться вертикально.

(А. Богданов). Откройте файл электронной таблицы 9-127.xls, содержащей в каждой строке три натуральных числа, являющиеся коэффициентами (a,b,c) квадратного уравнения ax²+bx+c=0. Коэффициенты a, b и с записаны соответственно в столбцах A, B и C электронной таблицы. Выясните, какое количество уравнений имеют два действительных корня.

(А. Богданов). Откройте файл электронной таблицы 9-127.xls, содержащей в каждой строке три натуральных числа, являющиеся коэффициентами (a,b,c) квадратного уравнения ax²+bx+c=0. Коэффициенты a, b и с записаны соответственно в столбцах A, B и C электронной таблицы. Выясните, какое количество уравнений не имеют действительных корней.

(А. Богданов). Откройте файл электронной таблицы 9-130.xls, содержащей в каждой строке три натуральных числа. Выясните, какое количество троек могут перестановкой образовать арифметическую прогрессию с не нулевой разностью прогрессии.

(А. Богданов). Откройте файл электронной таблицы 9-130.xls, содержащей в каждой строке три натуральных числа. Выясните, какое количество троек могут перестановкой образовать геометрическую прогрессию с отличным от единицы знаменателем прогрессии.

(А. Кабанов). Откройте файл электронной таблицы 9-132.xls, содержащей в каждой строке четыре натуральных числа – координаты двух точек на плоскости. Первые два числа в каждой строке – координаты x₁ и y₁ первой точки, третье и четвёртое – координаты x₂ и y₂ второй точки. Выясните, какое количество пар точек может являться концами отрезка, не пересекающего ни ось X, ни ось Y.

(А. Кабанов). Откройте файл электронной таблицы 9-132.xls, содержащей в каждой строке четыре натуральных числа – координаты двух точек на плоскости. Первые два числа в каждой строке – координаты x₁ и y₁ первой точки, третье и четвёртое – координаты x₂ и y₂ второй точки. Выясните, какое количество пар точек может являться концами отрезка, пересекающего ровно одну из осей X или Y.

(А. Кабанов). Откройте файл электронной таблицы 9-134.xls, содержащей в каждой строке четыре натуральных числа – координаты двух точек на плоскости. Первые два числа в каждой строке – координаты x₁ и y₁ первой точки, третье и четвёртое – координаты x₂ и y₂ второй точки. Определите количество пар точек, в которых обе точки лежат на осях координат.

(А. Кабанов). Откройте файл электронной таблицы 9-132.xls, содержащей в каждой строке четыре натуральных числа – координаты двух точек на плоскости. Первые два числа в каждой строке – координаты x₁ и y₁ первой точки, третье и четвёртое – координаты x₂ и y₂ второй точки. Выясните, какое количество пар точек может являться концами отрезка длиной не больше 5, пересекающего ось X или ось Y.

(А. Носкин) Исполнитель Черепашка перемещается на экране компьютера, оставляя след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует две команды: Вперёд n (где n — целое число), вызывающая передвижение Черепашки на n шагов в направлении движения; Направо m (где m — целое число), вызывающая изменение направления движения на m градусов по часовой стрелке. Запись Повтори k [Вперед n Направо m] означает, что последовательность команд в скобках повторится k раз.
Откройте файл электронной таблицы 9-136.xls, содержащей в каждой строке три натуральных числа, являющиеся последовательностью значений k, n, m. Выясните, какое количество троек чисел соответствует тому, что на экране появится правильный шестиугольник. В ответе запишите только число.

(А. Носкин) Исполнитель Черепашка перемещается на экране компьютера, оставляя след в виде линии. В каждый конкретный момент известно положение исполнителя и направление его движения. У исполнителя существует три команды: Вперёд n (где n — целое число), вызывающая передвижение Черепашки на n шагов в направлении движения; Направо m (где m — целое число), вызывающая изменение направления движения на m градусов по часовой стрелке; Налево х (где х — целое число), вызывающая изменение направления движения на х градусов против часовой стрелки. Запись Повтори k [Направо m Вперёд n Налево x] означает, что последовательность команд в скобках повторится k раз.
Откройте файл электронной таблицы 9-137.xls, содержащей в каждой строке четыре натуральных числа, являющиеся последовательностью значений k, m, n, х. Выясните, какое количество четверок чисел соответствует тому, что на экране появится правильный пятиугольник? В ответе запишите только число.

(П. Финкель). В файле электронной таблицы 9-138.xls содержатся целые числа – координаты трёх точек в формате X1, X2, X3, Y1, Y2, Y3. Найдите количество таких строк, где все три точки лежат в одной четверти координатной плоскости.

(П. Финкель). В файле электронной таблицы 9-138.xls содержатся целые числа – координаты трёх точек в формате X1, X2, X3, Y1, Y2, Y3. Найдите количество таких строк, где ровно две точки лежат в одной четверти координатной плоскости.

(М. Дунаев). В файле электронной таблицы 9-140.xls содержатся целые числа – координаты двух клеток шахматной доски. В столбцах A и C записаны номера вертикалей, а в столбцах B и D –номера горизонталей. Из-за ошибок ввода некоторые из координат могут оказаться меньше 1 или больше 8 – строки с такими данными учитывать не нужно. Определите, сколько существует пар клеток, таких что ладья может попасть с первой клетки на вторую одним ходом. Ладья не может ходить за пределы доски, а также остаться на той же клетке.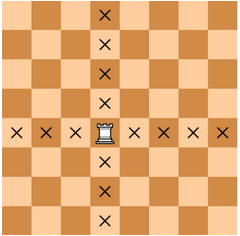

(М. Дунаев). В файле электронной таблицы 9-140.xls содержатся целые числа – координаты двух клеток шахматной доски. В столбцах A и C записаны номера вертикалей, а в столбцах B и D –номера горизонталей. Из-за ошибок ввода некоторые из координат могут оказаться меньше 1 или больше 8 – строки с такими данными учитывать не нужно. Определите, сколько существует пар клеток, таких что слон может попасть с первой клетки на вторую одним ходом. Слон не может ходить за пределы доски, а также остаться на той же клетке.

(М. Дунаев). В файле электронной таблицы 9-140.xls содержатся целые числа – координаты двух клеток шахматной доски. В столбцах A и C записаны номера вертикалей, а в столбцах B и D –номера горизонталей. Из-за ошибок ввода некоторые из координат могут оказаться меньше 1 или больше 8 – строки с такими данными учитывать не нужно. Определите, сколько существует пар клеток, таких что ферзь может попасть с первой клетки на вторую одним ходом. Ферзь не может ходить за пределы доски, а также остаться на той же клетке.

(М. Дунаев). В файле электронной таблицы 9-140.xls содержатся целые числа – координаты двух клеток шахматной доски. В столбцах A и C записаны номера вертикалей, а в столбцах B и D –номера горизонталей. Из-за ошибок ввода некоторые из координат могут оказаться меньше 1 или больше 8 – строки с такими данными учитывать не нужно. Определите, сколько существует пар клеток, таких что король может попасть с первой клетки на вторую одним ходом. Король не может ходить за пределы доски, а также остаться на той же клетке.

(М. Дунаев). В файле электронной таблицы 9-140.xls содержатся целые числа – координаты двух клеток шахматной доски. В столбцах A и C записаны номера вертикалей, а в столбцах B и D –номера горизонталей. Из-за ошибок некоторые из координат могут оказаться меньше 1 или больше 8 – такие данные учитывать не нужно. Определите, сколько существует пар клеток, таких что конь может попасть с первой клетки на вторую одним ходом. Конь не может ходить за пределы доски, а также остаться на той же клетке.

(Е. Джобс). В файле электронной таблицы 9-145.xls содержатся четверки целых положительных чисел – значения углов, выраженные в градусах. Сколько среди них таких четвёрок, которые могут быть углами выпуклого четырехугольника?
(Е. Джобс). В файле электронной таблицы 9-146.xls содержатся значения углов A, B, C, D, выраженные в градусах. Сколько среди них таких четвёрок, которые могут быть углами равносторонней трапеции с основаниями AD и BC?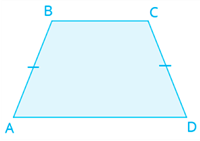

(Е. Джобс). В файле электронной таблицы 9-147.xls содержатся пары чисел – длины диагоналей ромба. Сколько среди них пар, которые соответствуют ромбам площадью 48 единиц?
(Е. Джобс). В файле электронной таблицы 9-148.xls содержатся пары чисел. Каждая пара характеризует серию экспериментов; первое число в паре – количество проведенных экспериментов, второе – количество положительных исходов в серии. Определите количество серий, в которых доля положительных исходов была выше, чем общая доля положительных исходов для всех приведённых испытаний.
(Е. Джобс). Свойства идеального газа, находящегося в адиабатическом процессе, подчиняются уравнению Менделеева-Клапейрона: pV = nRT, где p — давление, V — объём газа, n — количество вещества в молях, R — универсальная газовая постоянная, R ≈ 8,314 Дж/(моль⋅К), T — термодинамическая температура в Кельвинах.

В файле электронной таблицы 9-149.xls содержатся значения для p, V и T, причём в каждой строке одно из этих значений пропущено. Значение n, одинаковое для всех строк, задано в ячейке F1. Определите недостающие данные и определите значение минимальной температуры в Кельвинах. В ответе укажите только целую часть найденного значения.

(А. Рогов) В файле электронной таблицы 9-150.xls содержатся тройки натуральных чисел. Сколько среди них троек, в которых квадрат максимального из трёх чисел больше удвоенного произведения двух других чисел в строке?
(А. Рогов) В файле электронной таблицы 9-150.xls содержатся тройки натуральных чисел. Сколько среди них троек, в которых куб минимального из трёх чисел больше утроенного произведения двух других чисел в строке?
(А. Рогов) В файле электронной таблицы 9-152.xls в каждой строке содержатся четыре натуральных числа. Сколько среди них строк, в которых квадрат суммы максимального и минимального чисел в строке больше суммы квадратов двух оставшихся?
(А. Рогов) В файле электронной таблицы 9-152.xls в каждой строке содержатся четыре натуральных числа. Сколько среди них строк, в которых модуль куба разности максимального и минимального чисел в строке не превышает квадрат суммы двух оставшихся?
(А. Рогов) В файле электронной таблицы 9-154.xls в каждой строке содержатся пять натуральных числа. Сколько среди них строк, в которых квадрат суммы максимального и минимального чисел в строке больше суммы квадратов трёх оставшихся?
(А. Рогов) В файле электронной таблицы 9-154.xls в каждой строке содержатся пять натуральных числа. Сколько среди них строк, в которых квадрат произведения максимального и минимального чисел в строке больше утроенного произведения трех оставшихся?
(А. Рогов) В файле электронной таблицы 9-154.xls в каждой строке содержатся пять натуральных числа. Сколько среди них строк, в которых квадратный корень произведения максимального и минимального чисел в строке больше кубического корня из произведения трех оставшихся?
(PRO100 ЕГЭ) В файле электронной таблицы 9-157.xls в каждой строке содержатся шесть натуральных чисел. Определите количество строк, в которых числа можно разбить на три пары, состоящие из одинаковых чисел. Пример: шестёрку 1 2 3 3 1 2 можно разбить на пары 1-1 2-2 3-3.

1 2 3