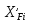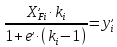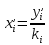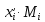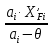Расчет отбензиневающей колонны. Задание на курсовой проект по дисциплине Первичная переработка нефти и газа Ф. И. О. Юрченко Р. Р. Тема Технологический расчёт отбензинивающей колонны установки атмосферной перегонки нефти мощностью 4,8 млн т в год
 Скачать 243.74 Kb. Скачать 243.74 Kb.
|
|
Задаёмся значением мольной доли отгона 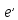 в следующих пределах: в следующих пределах: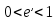 Проверяем тождество: 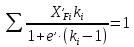 Если тождество не выполняется, задаёмся новым значением 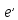 . .Расчёт показал, что мольная доля отгона 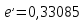 Средний молекулярный вес паровой фазы сырья: 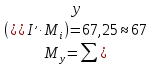 Средний молекулярный вес жидкой фазы сырья: 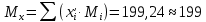 Массовая доля отгона сырья:  Где 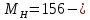 средний молекулярный вес сырья (нефти). средний молекулярный вес сырья (нефти).Таблица 6.2 Расчёт доли отгона сырья на входе в колонну
7. МИНИМАЛЬНОЕ ФЛЕГМОВОЕ ЧИСЛО Минимальное флегмовое число  определяем по уравнениям Андервуда: определяем по уравнениям Андервуда: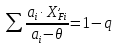 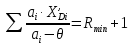 где 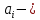 коэффициент относительной летучести коэффициент относительной летучести 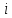 -го компонента по отношению к ключевому компоненту: -го компонента по отношению к ключевому компоненту: где  - давление насыщенных паров при температуре ввода сырья - давление насыщенных паров при температуре ввода сырья 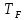 ; ;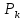 – давление насыщенных паров ключевого компонента, которым задавались в начале расчета, т.е. 3-го компонента 62-85 – давление насыщенных паров ключевого компонента, которым задавались в начале расчета, т.е. 3-го компонента 62-85 ; ;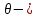 корень уравнения Андервуда. Обычно его величина находится между значениями корень уравнения Андервуда. Обычно его величина находится между значениями 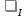 ключевых компонентов (в нашем случае между 3 и 4 компонентами). В общем случае, при увеличении левая часть уравнения возрастает. ключевых компонентов (в нашем случае между 3 и 4 компонентами). В общем случае, при увеличении левая часть уравнения возрастает.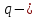 отношение количества тепла отношение количества тепла 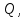 которое надо сообщить сырью, чтобы перевести его в парообразное состояние, к скрытой теплоте испарения сырья которое надо сообщить сырью, чтобы перевести его в парообразное состояние, к скрытой теплоте испарения сырья  : :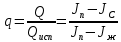 где  – энтальпия сырья при температуре ввода; – энтальпия сырья при температуре ввода; – энтальпия насыщенных паров сырья; – энтальпия насыщенных паров сырья; – энтальпия жидкой части сырья при температуре кипения. – энтальпия жидкой части сырья при температуре кипения.При расчёте минимального флегмового числа возможны следующие варианты: Если сырьё вводится при температуре кипения, тогда 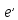 = 0 и = 0 и 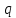 = 1. = 1.Если сырьё вводится в виде холодной жидкости, не доведенной до температуры кипения, тогда 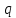 > 1. > 1.Если сырьё вводится в виде насыщенных паров, то 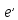 = 1 и = 1 и 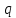 = 0. = 0.Если сырьё вводится в виде перегретых паров, то 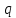 < 0. < 0.Если сырьё вводится в виде парожидкостной смеси, то 0 < 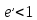 и и 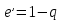 В нашем случае сырьё вводится в парожидкостном состоянии, поэтому: 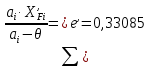 Давления насыщенных паров компонентов при температуре  . рассчитаны ранее. Определяем коэффициенты относительной летучести. Например, для первого компонента: . рассчитаны ранее. Определяем коэффициенты относительной летучести. Например, для первого компонента: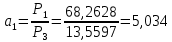 Для пятого компонента: 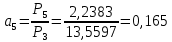 Корень уравнения 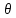 находится в пределах: находится в пределах: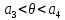 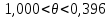 Таблица 7.1 Расчёт минимального флегмового числа
Методом подбора определяем, что корень уравнения Андервуда равен:  Значение корня  подставляем во второе уравнение: подставляем во второе уравнение: Минимальное флегмовое число: 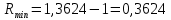 8. ОПТИМАЛЬНОЕ ФЛЕГМОВОЕ ЧИСЛО. ОПТИМАЛЬНОЕ ЧИСЛО ТЕОРЕТИЧЕСКИХ ТАРЕЛОК Рассмотрим два способа расчёта оптимального флегмового числа. Графический способ Джиллиленда. Задаёмся предварительно коэффициентом избытка флегмы 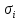 = 1,1-2,5 с шагом 0,1. Если при данных значениях не будет получен минимум на построенной впоследствии кривой, следует увеличить значение = 1,1-2,5 с шагом 0,1. Если при данных значениях не будет получен минимум на построенной впоследствии кривой, следует увеличить значение 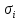 . При каждом значении . При каждом значении 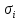 рассчитываем: рассчитываем:Флегмовое число: 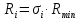 Например:  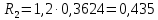 Параметр 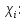  Например: 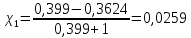  Параметр 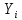 : :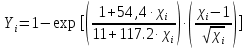 Например: 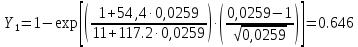 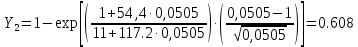 Число теоретических тарелок 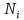 : : Например:  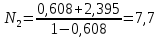 Величину 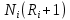 . Например: . Например: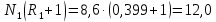 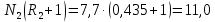 Строим график  Рисунок 8.1. Минимум на полученной кривой соответствует оптимальному флегмовому числу: Рисунок 8.1. Минимум на полученной кривой соответствует оптимальному флегмовому числу: . .При данном значении оптимального флегмового числа определяем оптимальное число теоретических тарелок:  Результаты расчётов приведены в таблице 8.1. Аналитический вариант расчёта (по приближённым уравнениям). 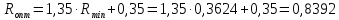  Таким образом, оба способа дают довольно близкие результаты. Принимаем к дальнейшим расчётам результаты более точного графического способа. N 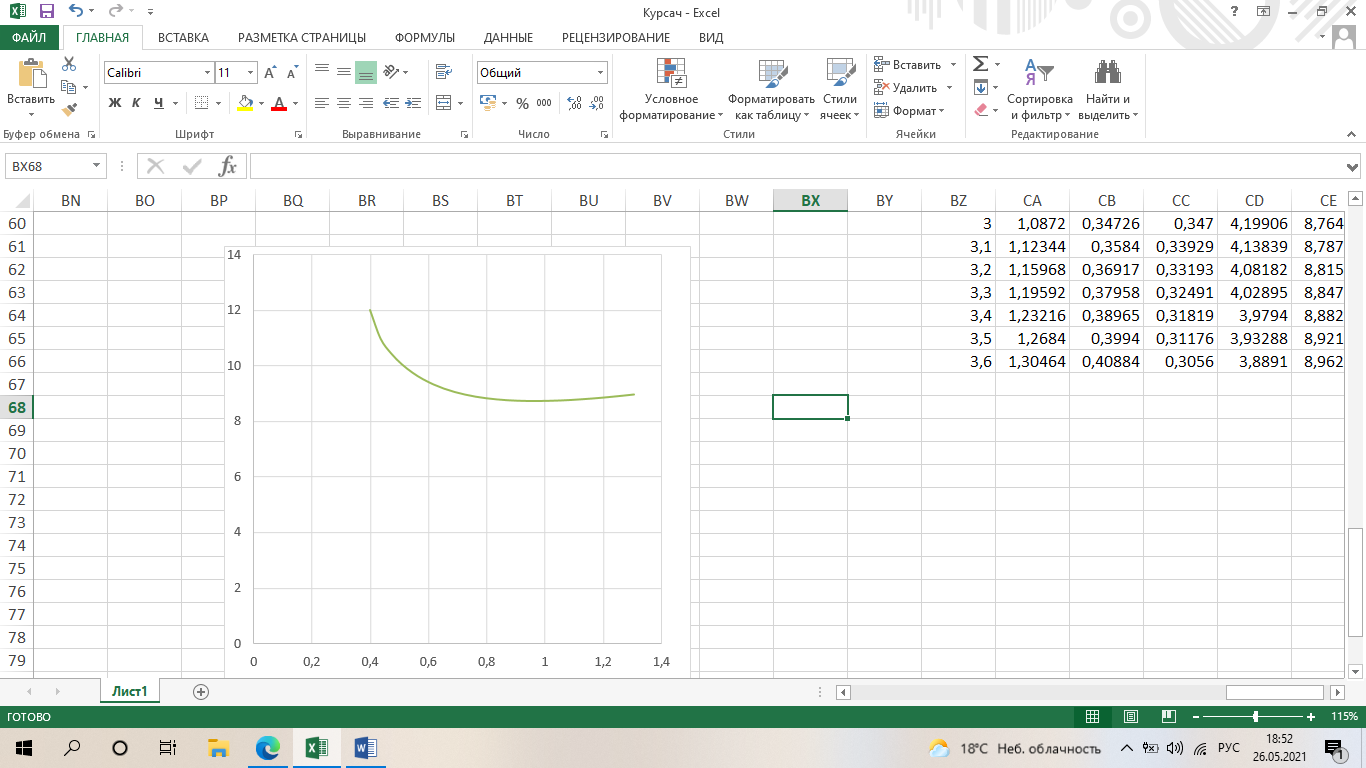 i(Ri+1) i(Ri+1)Ri Рис.8.1. График зависимости |