Сборный консольный железобетонный перепад. Задание по дисциплине инженерные конструкции к расчетно графическим работам 1 и 2
 Скачать 0.53 Mb. Скачать 0.53 Mb.
|
1.3. РАСЧЕТ РИГЕЛЯ РАМЫ ПО ТРЕЩИНОСТОЙКОСТИВ курсовом проекте следует проверить трещиностойкость пролетного сечения ригеля. Расчет начинают с определения категории требований к трещиностойкости пролетного сечения и допустимой ширины раскрытия трещин. В контрольной работе для ненапряженного ригеля определяем ширину раскрытия трещин и сопоставляем ее с допускаемой. Расчет по раскрытию трещин производят из условия acrc ≤ acrc,ult (5 где acrc - ширина раскрытия трещин от действия внешней нагрузки; acrc,ult-предельно допустимая ширина раскрытия трещин. Значения acrc,ult принимают равными: а) из условия сохранности арматуры (для любых конструкций) 0,3 мм - при продолжительном раскрытии трещин; 0,4 мм - при непродолжительном раскрытии трещин; б) из условия ограничения проницаемости конструкций (для конструкций, подверженных непосредственному давлению жидкостей, газов, сыпучих тел) 0,2 мм - при продолжительном раскрытии трещин; 0,3 мм - при непродолжительном раскрытии трещин. Расчет по раскрытию трещин не производится, если соблюдается условие М < Mcrc, где М - момент от внешней нагрузки относительно оси, нормальной к плоскости действия момента и проходящей через центр тяжести приведенного поперечного сечения элемента; при этом учитываются все нагрузки (постоянные и временные) с коэффициентом надежности по нагрузке γf = 1; Mcrc - момент, воспринимаемый нормальный сечением элемента при образовании трещин. Момент образования трещин Мсrс определяют по формуле: 𝑀crc= 𝑅bt,ser ∗ 𝑊pl Для этого определяем геометрические характеристики приведенного сечения при 𝛼 = 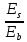 𝛼 = 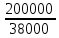 = 5,26 = 5,26Ared = bh + aAs Ared=20*60+6*15,27 = 1291,6 см2 𝑦t = 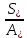 𝑦t = 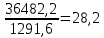 см см𝑆red = 𝑏 ∗ ℎ ∗ 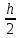 + 𝛼 ∗ 𝐴s ∗ a + 𝛼 ∗ 𝐴s ∗ a𝑆red = 20 ∗ 60 ∗ 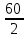 + 5,26 ∗ 15,27 ∗ 6 = 36482,2 см3 + 5,26 ∗ 15,27 ∗ 6 = 36482,2 см3𝐼red= 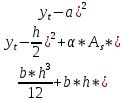 𝐼red= 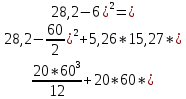 397665 см 397665 см𝑊red= 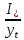 𝑊red= 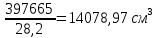 Неупругие деформации растянутого бетона учитываются путем умножения W на коэффициент γ, равный 1,30, т.е. 𝑊pl = 1,3𝑊 Wpl = 1,3*14078,97 = 18302,7 см3 Mcrc = 18302,7 * 0,245 = 4484,2 кНсм = 44,84 кНм М < Mcrc 313,73<44,84 – условие не выполняется Так как 𝑀crc˂ 𝑀, то расчет по раскрытию трещин производим. необходим. Напряжение в арматуре σs определяем по формуле: 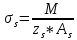 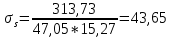 Рабочая высота сечения ho = h – а =60-5,41=54,59 см Коэффициент приведения 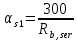 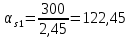 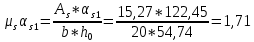 Тогда при 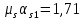 и 𝛾 = 0 из графика на рис. 4.3.1.1. находим коэффициент ζ=0,86. и 𝛾 = 0 из графика на рис. 4.3.1.1. находим коэффициент ζ=0,86. Тогда плечо внутренней пары сил равно 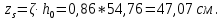 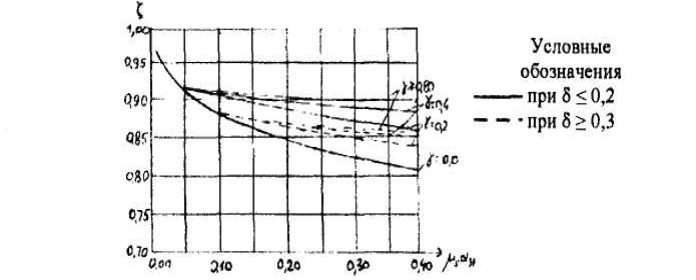 Рис.4.3.1.1 График коэффициента ζ = zs /ho для определения плеча внутренней пары сил при расчете по раскрытию трещин изгибаемых элементов Значение базового расстояния между трещинами ls определяется по формуле 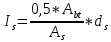 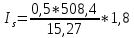 =30 см =30 см 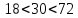 – условие выполняется – условие выполняетсяи принимают не менее 10ds и 100 мм и не более 40ds и 400 мм (для элементов с рабочей высотой поперечного сечения не более 1 м). 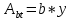 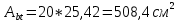 Здесь Abt - площадь сечения растянутого бетона. При этом высота растянутой зоны бетона принимается не менее 2α и не более 0,5h. Для прямоугольных сечений высоту растянутой зоны бетона допускается определять по формуле: 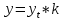 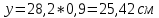 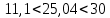 – условие выполняется – условие выполняется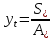 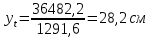 где yt - высота растянутой зоны бетона, определяемая как для упругого материала при коэффициенте приведения арматуры к бетону, α = Еs/Еb; к - поправочный коэффициент, для прямоугольных сечений равный 0,90; Значение ψs определяют по формуле: 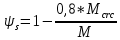 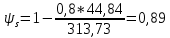 и принимают не менее 0,2. Ширину раскрытия нормальных трещин определяют по формуле 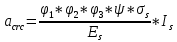 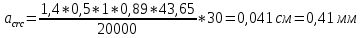 где σs - напряжение в продольной растянутой арматуре в нормальном сечении с трещиной от соответствующей внешней нагрузки; ls - базовое (без учета влияния вида поверхности арматуры) расстояние между смежными нормальными трещинами; ψs - коэффициент, учитывающий неравномерное распределение относительных деформаций растянутой арматуры между трещинами; φ1 - коэффициент, учитывающий продолжительность действия нагрузки и принимаемый равным: 1,0 - при непродолжительном действии нагрузки; 1,4 - при продолжительном действии нагрузки; φ2 - коэффициент, учитывающий профиль продольной арматуры и принимаемый равным: 0,5 - для арматуры периодического профиля (классов А300, А400, А500, В500); 0,8 - для гладкой арматуры (класса А240); φ3 - коэффициент, учитывающий характер нагружения и принимаемый равным 1,0 - для изгибаемых и внецентренно сжатых элементов; |
