Выпарка. 4 расчет выпарного аппарата. 4. 1 Определение поверхности теплопередачи выпарного аппарата

• Название: 4. 1 Определение поверхности теплопередачи выпарного аппарата
• Анкор: Выпарка
• Дата: 14.10.2020
• Размер: 0.53 Mb.
• Имя файла: 4 расчет выпарного аппарата.doc
• Тип: Документы; #142776

4 Расчет выпарного аппарата

4.1 Определение поверхности теплопередачи выпарного аппарата

Поверхность теплопередачи каждого корпуса выпарной установки определяют по основному уравнению теплопередачи:

, (4.1)

где, – тепловая нагрузка, Вт;

– коэффициент теплопередачи, Вт/(м²·К);

– полезная разность температур, К.

Для определения тепловых нагрузок, коэффициентов теплопередачи, полезных разностей температур необходимо знать распределение упариваемой воды, концентрацию растворов и их температур кипения по корпусам. Эти величины находятся методом последовательных приближений.

Первое приближение:

Производительность установки по выпариваемой воде определяют из уравнения материального баланса:

, (4.2)

где, – массовый расход испаряемого растворителя, кг/с;

– массовый расход конечного раствора, кг/с;

– массовая доля растворенного вещества в начальном растворе, кг/кг;

– массовая доля растворенного вещества в конечном растворе, кг/кг.

Получаем:



Определим массовый расход начального раствора:

, (4.3)



4.1.1 Концентрации упариваемых растворов

В первом приближении на основании практических данных принимают, что производительность по выпариваемой воде распределяется между корпусами в соответствии с соотношением:



где – производительность по выпариваемой воде в первом аппарате, кг/с;

– производительность по выпариваемой воде во втором аппарате, кг/с.

Тогда получаем:

(4.4)







Рассчитываем составы растворов в корпусах по формуле:

, (4.5)

где – концентрация раствора, кг/кг

Получаем:





4.1.2 Выбор давления греющего пара

Рассчитываем температуру греющего пара по формуле:

(4.6)

где – температура греющего пара, ;

– температура конденсации, ;

– температурная депрессия при атмосферном давлении при , ;

– гидравлическая депрессия, .

Исходя из концентрации выпариваемого компонента в последнем корпусе, находим температурную депрессию [1]: .

Примем, что гидравлическая депрессия во всех корпусах равна 1ºС.

Примем, что .

= 54 при = 15 кПа [1]



Эта температура греющего пара соответствует давлению греющего пара равному [6]. Приводим к стандартному [1].

Находим общий перепад давлений в установке:

(4.7)

где – давление греющего пара, МПа;

– давление в барометрическом конденсаторе, МПа.



Давления греющих паров в корпусах равны:

,

(4.8)



По давлениям паров находим их температуры и энтальпии [6] и заносим в таблицу 4.1.
Таблица 4.1 – Температуры и энтальпии греющих паров выпарной установки

Р, МПа	t, ºC	I, кДж/кг
Рг1=0,55	tг1=155,7	I1=2694,9
Рг2=0,2825	tг2=131,9	I2=2687,8
Рбк=0,015	Tбк=54	I3=2598,9

Температура кипения раствора в корпусе отличается от температуры греющего пара в последующем корпусе на сумму температурных потерь от температурной, гидростатической и гидродинамической депрессий.

Гидродинамическая депрессия обусловлена потерей давления пара на преодоление гидравлических сопротивлений трубопроводов при переходе из корпуса в корпус. Принимаем гидравлическую депрессию равной 1ºС.

Температуры вторичных паров в корпусах рассчитываются по формуле:

(4.9)

где Δ"' – гидравлическая депрессия.

Принимаем гидравлическую депрессию равной 1ºС.





По температурам вторичных паров определим их давления [6]. Результаты сведем в таблицу 4.2.

Таблица 4.2 – Температуры и давления вторичных паров выпарной установки

tвп, ºC	Рвп, МПа	r, кДж/кг
tвп1=132,9	Рвп1=0,2948	=2165,8
tвп2=55	Рвп2=0,01575	=2369,7

Ориентировочно оценим поверхность теплопередачи выпарного аппарата Fор. Поверхность теплопередачи i– го корпуса ориентировочно рассчитывается по формуле:

(4.10)

где ri– теплота парообразования вторичного пара при температуре вторичного пара, Дж/кг:

– ориентировочное значение относительной тепловой нагрузки, .

Примем [3]





По ГОСТ 11987-81 [7] трубчатые аппараты с естественной циркуляцией и вынесенной зоной кипения (тип 1, исполнение 2) состоят из кипятильных труб высотой 4 и 5 м при диаметре = 38 мм и толщине стенки δ_ст = 2 мм. Принимаем высоту кипятильных труб Н = 4м.

Определим температурную депрессию по уравнению:

(4.11)

где Т – температура паров в среднем слое кипятильных труб, К;

– температурная депрессия при атмосферном давлении и при , °С.

По справочной литературе [1] определим = 8

Получаем:





Сумма температурных депрессий равна:



Температуры кипения растворов в корпусах рассчитываем по формуле:

(4.12)

Находим температуры кипения растворов:





4.1.3 Расчет температуры перегрева раствора

Расчет температуры перегрева раствора производится по формуле:

(4.13)

Расчет температуры перегрева для 1-ого корпуса: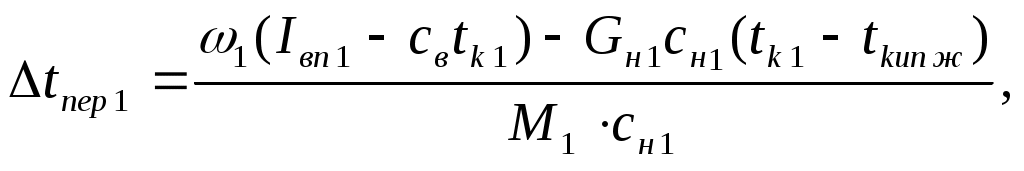



где – энтальпия вторичного пара в 1 корпусе при , кДж/кг;

св – теплоемкость воды при , кДж/кг·К;

– массовый расход раствора на входе в 1 корпус, кг/с;

– теплоемкость раствора при , кДж/кг·К;

tкип ж – температура кипения раствора при хн = 14%, ;

– масса циркулирующего раствора в 1 корпусе, кг/с. Рассчитывается по формуле:

,

где – плотность раствора при и , ;

v – скорость циркулирующего раствора, м/с. В аппаратах с естественной циркуляцией v = 0,6 – 0,8 м/с. Принимаем v = 0,7 м/с.

S1 – сечение потока в аппарате, м². Рассчитывается по формуле:

,

где – внутренний диаметр трубы, м.

= 0,038 м

.

Отсюда рассчитаем массу циркулирующего раствора:

= 1075 [6]

,

Получаем:

= 2737,7 кДж/кг [6]

с_в = 4,292 кДж/кг·К [1]

= 3,976 кДж/кг·К [6]

tкип ж = 102 [6]



Расчет температуры перегрева для 2-ого корпуса: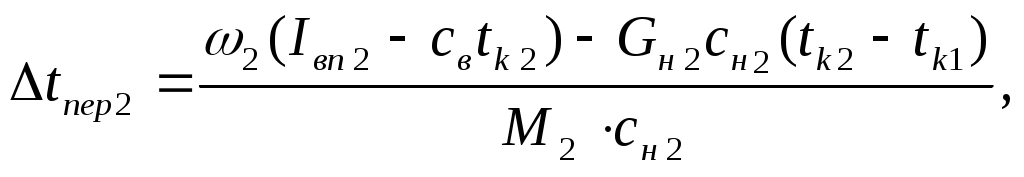



где – энтальпия вторичного пара в 2 корпусе при , кДж/кг;

св– теплоемкость воды при , кДж/кг·К;

– массовый расход раствора на входе во 2 корпус, кг/с. Рассчитывается по формуле:

, (4.14)

.

– теплоемкость раствора при , кДж/кг·К;

– масса циркулирующего раствора во 2 корпусе, кг/с. Рассчитывается по формуле:

, (4.15)

– плотность раствора при и , ;

– сечение потока в аппарате, м². Рассчитывается по формуле:

, (4.16)

.

Отсюда рассчитаем массу циркулирующего раствора:

= 1183 [6]

,

Получаем:

= 2639,3 кДж/кг [1]

св = 4,19 кДж/кг [1]

= 3,484 кДж/кг [6]



4.1.4 Расчет полезной разности температур

Полезные разности температур по корпусам находим по формуле:

(4.17)

где – полезная разность температур в 1 корпусе, .

Получаем:





Общая полезная разность температур равна:



4.1.5 Определение тепловых нагрузок

Расход греющего пара в 1-й корпус, производительность каждого корпуса по выпаренной воде и тепловые нагрузки по корпусам определим путем совместного решения уравнений тепловых балансов по корпусам и уравнения баланса по воде для всей установки:

(4.18)

(4.19)

(4.20)

где 1,03 – коэффициент, учитывающий 3% потери тепла в окружающую среду;

с₁, с₂ – теплоемкости растворов в корпусах, кДж/(кг·К);

– расход греющего пара, кг/с;

– тепловые нагрузки по корпусам, кВт;

Q_1конц,Q_2конц –теплоты концентрирования по корпусам, кВт;

– энтальпии растворов в корпусах, кДж/кг;

t_н – температура кипения исходного раствора, °C;

Принимаем, что .

Поскольку Q_1конц,Q_2конц малые величины, то можно ими пренебречь, получим систему уравнений:

= 686,516 кДж/кг [6]

= 589, 5 кДж/кг [6]





Решение этой системы уравнений дает следующие результаты: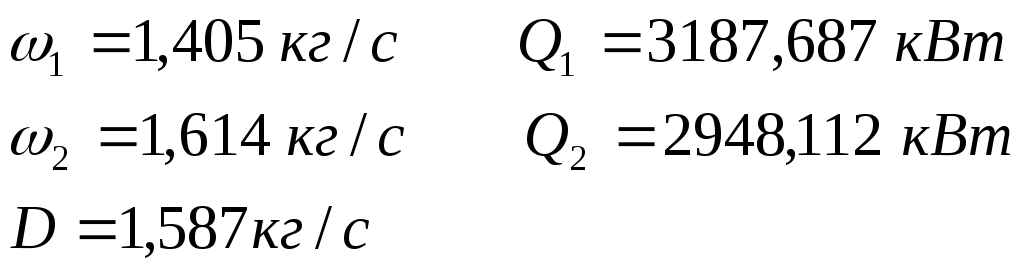



Результаты расчета сведем в таблицу 4.3:

Таблица 4.3 – Результаты расчета

Параметр	Корпус
	1	2
производительность по испаряемой воде w, кг/с	1,405	1,614
концентрация раствора х, %	20,52	42,01
давление греющих паров Ргп, МПа	0,55	0,2825
температура греющих паров tгп, ºС	155,7	131,9
температурные потери, град	10,81	24,392
температура кипения раствора tк, ºС	142,71	78,392
полезная разность температур, град	11,42	50,972

4.2 Выбор конструкционного материала

Выбираем конструкционный материал, стойкий в среде кипящего раствора в интервале изменения концентраций от 10 до 40% [5]. В этих условиях химически стойкой является сталь марки Х21Н5Т. Скорость коррозии ее не менее 0,1 мм/год, коэффициент теплопроводности = 16,748 Вт/м·К.

4.3 Расчет коэффициентов теплопередачи

Коэффициент теплопередачи для первого корпуса определяют по уравнению аддитивности термических сопротивлений: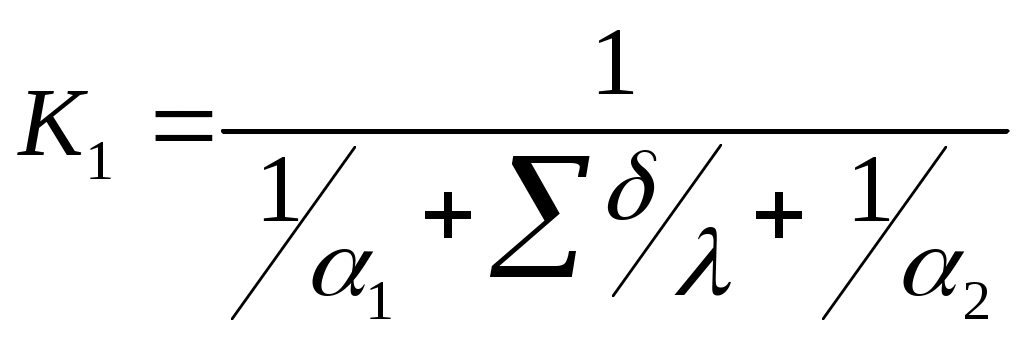

, (4.21)

где – коэффициент теплоотдачи;

– суммарное термическое сопротивление, м²·К/Вт.

, (4.22)

где – термическое сопротивление стенки, м²·К/Вт;

– термическое сопротивление загрязнений стенки для воды среднего качества, м²·К/Вт.

Получим:

= 0,002 м [1]

= 16,748 [1]



Коэффициент теплоотдачи от конденсирующегося пара к стенке равен: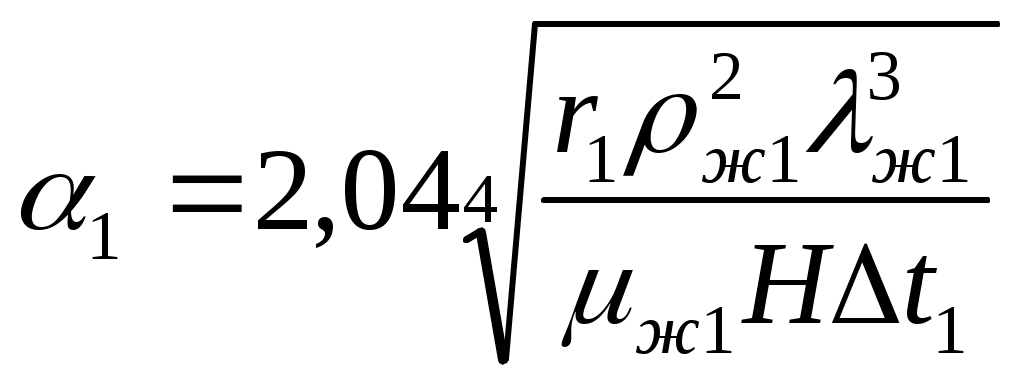

, (4.23)

где – коэффициент теплоотдачи от конденсирующегося пара к стенке.

Физические характеристики конденсата, входящие в коэффициент теплоотдачи, находим при температуре пленки, равной:

, (4.24)

где – разность температур конденсации пар и стенки, °С. в первом приближении. Примем, что = 2,0 °С, тогда:



где – теплота конденсации греющего пара, Дж/кг;

– плотность конденсата при средней температуре пленки, кг/м³;

– теплопроводность конденсата при средней температуре пленки, Вт/(м·К);

– вязкость конденсата при средней температуре пленки, Па·с;

– разность температур конденсации пара и стенки, град.

Расчет коэффициента ведут методом последовательных приближений, тогда:

= 2098 кДж/кг [1]

= 911,8 кг/м³ [1]

= 0,682 Вт/(м·К) [1]

= Па·с [1]



Для установившегося процесса передачи тепла справедливо уравнение: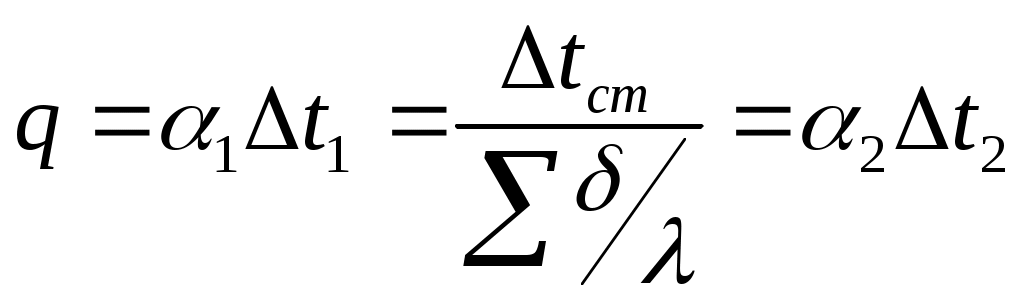

, (4.25)

где q– удельная тепловая нагрузка, Вт/м²;

– перепад температур на стенке, град;

– разность между температурой стенки со стороны раствора и температурой нагретого раствора, град.

Из этого уравнения следует:

, (4.26)

Получаем:



Рассчитываем разность между температурой стенки со стороны раствора и температуры нагретого раствора по формуле:

, (4.27)

Получаем:



Коэффициент теплоотдачи от стенки к раствору для его нагрева, без изменения агрегатного состояния, в вертикальных трубках находится по формуле:

, (4.28)

где Nu – критерий Нуссельта. Рассчитывается по уравнению:

, (4.29)

Физические характеристики растворов, входящие в критерии подобия, находим при средней температуре потока, равной

, (4.30)



Pr – критерий Прандтля. Рассчитывается по формуле:

, (4.31)

где с – теплоемкость раствора при t_ср, Дж/кг·К;

– вязкость раствора, Па·с;

– теплопроводность воды при t_ср, Вт/м·К.

d_вн – внутренний диаметр трубы, м;

Re – критерий Рейнольдса. Рассчитывается по формуле:

, (4.32)

– плотность раствора при t_ср, кг/м³.

Физические свойства нагретых растворов NaOH [6] приведены в таблице 4.4.

Таблица 4.4 – Физические свойства кипящего раствора NaOH

Параметр	Корпус
	1	2
1	2	3
теплопроводность раствора, Вт/(м·К)	0,682	0,671
плотность раствора, кг/м3	1122	1407
теплоемкость раствора, Дж/(кг·К)	3859	3433
вязкость раствора, Па·с	0,447·10-3	4,150·10-3

Подставляя численные значения, получаем:



Проверим правильность первого приближения по равенству удельных тепловых нагрузок:





Как видно q^/≠q^//, проводим второе приближение, примем .

Рассчитываем коэффициент теплоотдачи, пренебрегая изменением свойств конденсата при изменении температуры на градус:



Получим:





Проверим правильность второго приближения по равенству удельных тепловых нагрузок:







Как видно q^/≈q^//, поэтому рассчитываем коэффициент К₁: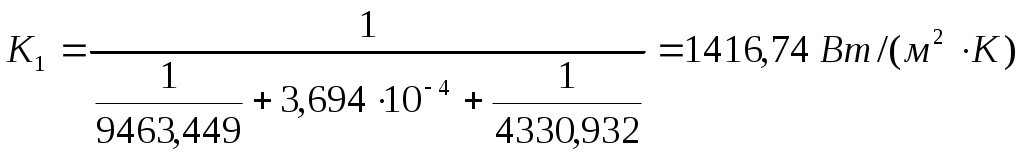



Пользуясь формулами приведенными ранее, рассчитываем коэффициент теплопроводности во втором корпусе, для этого находим коэффициент теплопередачи от конденсирующегося пара к стенке, принимая что = 2.0 град:



= 2173 кДж/кг [1]

= 934,2 кг/м³ [1]

= 0,681 Вт/(м·К) [1]

= Па·с [1]











= 0,671 Вт/(м·К) [6]

= 1407 кг/м³ [6]

= Па·с [6]



Как видно q^/≠q^//, проводим второе приближение, примем .

Примем во внимание изменение физических свойств конденсата при изменении температуры на 6°С:



= 2179 кДж/кг [1]

= 936,3 кг/м³ [1]

= 0,681 Вт/(м·К) [1]

= Па·с [1]













Как видно q^/≈q^//, поэтому рассчитываем коэффициент К₂: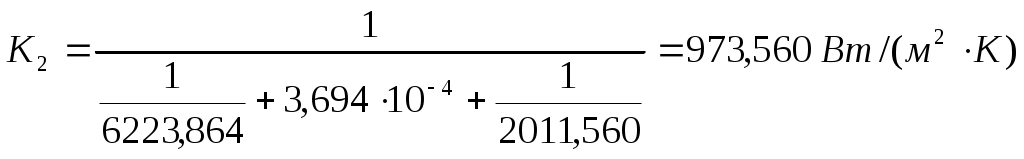



4.4 Распределение полезной разности температур

Полезные разности температур в корпусах установки находим из условия равенства их поверхностей теплопередачи: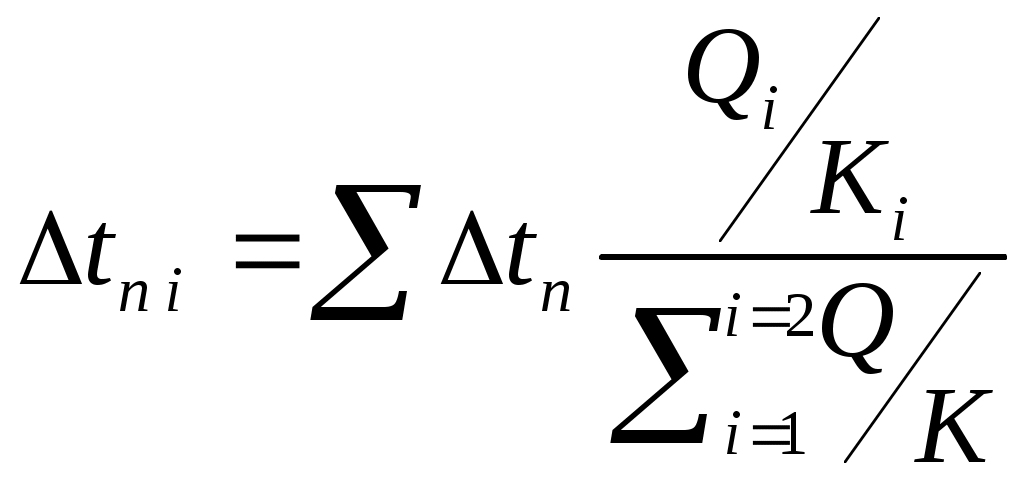

, (4.33)

где, – полезная разность температур, °C;

– тепловая нагрузка, кВт;

– коэффициент теплопередачи для i-того корпуса.

Подставляя численные значения в формулу, получаем: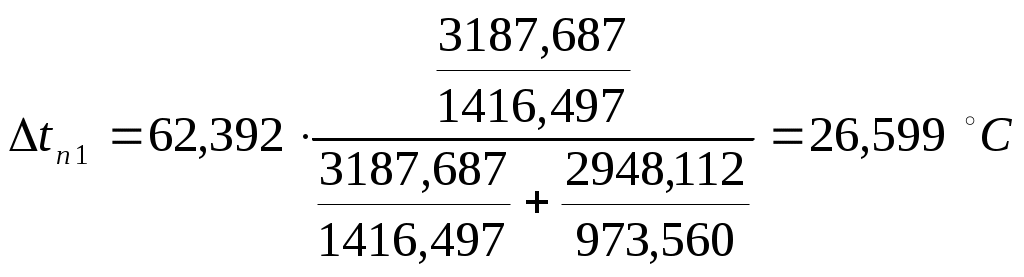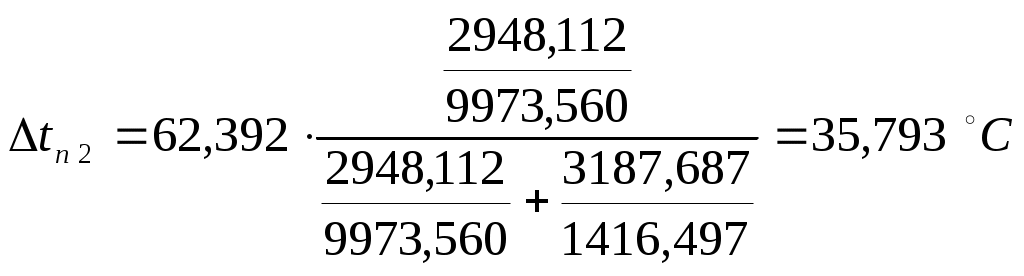





Проверим общую полезную разность температур установки:

(4.34)



Рассчитываем поверхность выпарных аппаратов по формуле:

(4.35)

Подставляя численные значения в формулу получаем:





Найденные значения мало отличаются от ориентировочно определенной раннее поверхности F_ор . Коррективы в изменение конструктивных размеров аппаратов вводиться не будут.

Сравнение распределенных из условий равенства поверхностей теплопередачи и предварительно рассчитанных значений полезных разностей температур Δt_п представлено в таблице 4.5.

Таблица 4.5 – Сравнение распределенных Δt_п

Корпус	1	2
в 1-м приближении, °С	11,42	30,972
предварительно рассчитанные ,°С	26,599	35,793