Физика. Лекция 3. Динамика твердого тела

• Название: Динамика твердого тела
• Анкор: Физика
• Дата: 30.03.2022
• Размер: 376 Kb.
• Имя файла: Лекция 3.doc
• Тип: Глава; #429977

Глава 7. Динамика твердого тела

7.1. Момент инерции

Момент инерции тела — мера инертности твердых тел при вращательном движении. Его роль такая же, что и массы при поступательном движении.

Моментом инерции системы (тела) относительно данной оси называется физическая величина, равная сумме произведений масс nматериальных точек системы на квадраты их расстоянии до рассматриваемой оси (рис. 7.1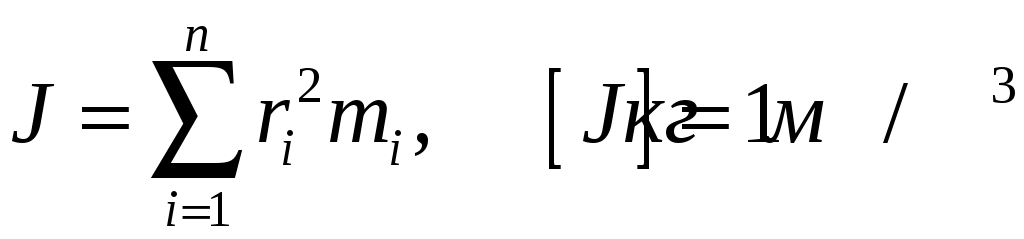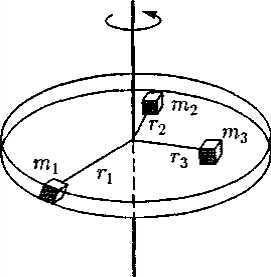.1):



Рис. 7.1.1.

В случае непрерывного распределения масс эта сумма сводится к интегралу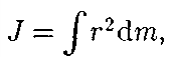



Момент инерции — величина аддитивная: момент инерции тела относительно некоторой оси равен сумме моментов инерции частей тела относительно той же оси.

В качестве примера найдем момент инерции однородного сплошного цилиндра высотой hи радиусом Rотносительно его геометрической оси (рис. 7.1.2). Разобьем цилиндр на отдельные полые концентрические цилиндры бесконечно малой толщины dr с внутренним радиусом r и внешним r+ dr.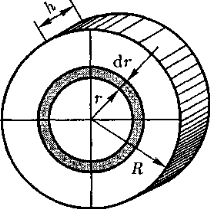

Рис. 7.1.2

Момент инерции каждого полого цилиндра, массой



Пологая, что плотность материала цилиндра 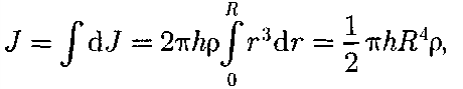, можно записать

, . Тогда момент инерции сплошного цилиндра



Т.к. масса цилиндра 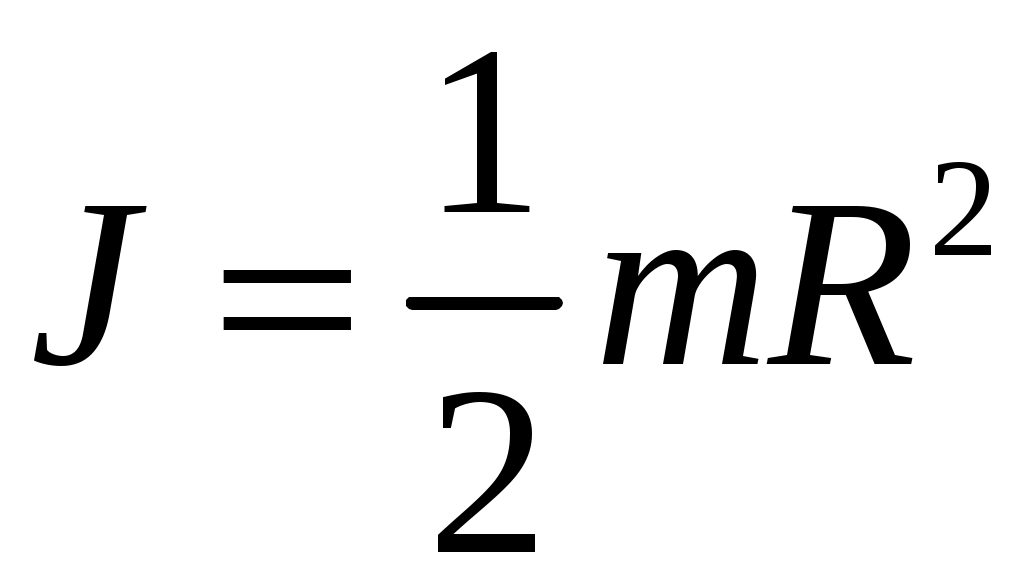, то .




Таб. 7.1.1. Моменты инерции некоторых однородных тел

Если известен момент инерции тела относительно оси, проходящей через его центр масс, то момент инерции относительно любой другой параллельной оси определяется теоремой Штейнера: момент инерции тела J относительно произвольной оси равен моменту его инерции относительно параллельной оси, проходящей через центр масс С тела, сложенному с произведением массы тела на квадрат расстояния между осями:


7.2. Кинетическая энергия вращения
Рассмотрим абсолютно твердое тело, вращающееся около неподвижной оси z, проходящей через него. Мысленно разобьем это тело на маленькие объемы с элементарными массами 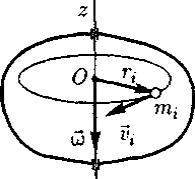находящиеся на расстоянии от оси. При вращении твердого тела относительно неподвижной оси отдельные его элементарные объемы массами опишут окружности различных радиусов и будут иметь различные линейные скорости .

Рис. 7.2.1.

Для скоростей вращающегося тела справедливо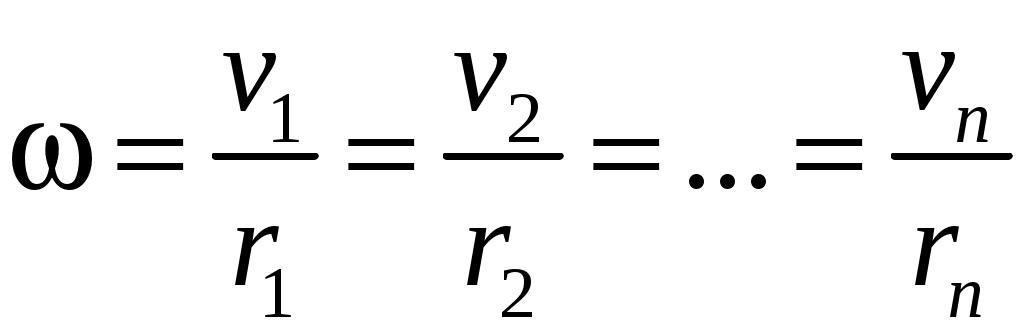

(7.2.1)

Кинетическую энергию вращающегося тела найдем как сумму кинетических энергий его элементарных объемов: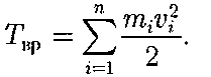



Используя (7.2.1) получим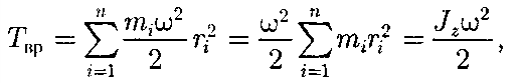



где момент инерции тела относительно оси .

Таким образом, кинетическая энергия вращающегося тела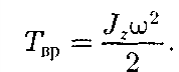



(Аналогия с поступательным движением)

В случае плоского движения тела, например цилиндра, скатывающегося с наклонной плоскости без скольжения, энергия движения складывается из энергии поступательного движения и энергии вращения: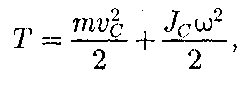



7.3. Уравнение динамики вращательного движения твердого тела.
Моментом силы относительно неподвижной точки О называется физическая величина М, определяемая векторным произведением радиуса-вектора 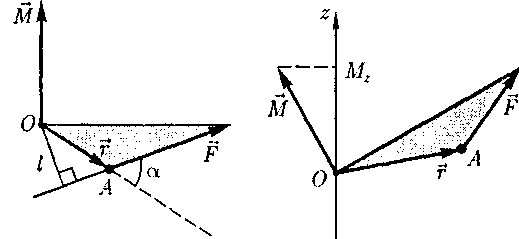, проведенного из точки О в точку А приложения силы, на силу (рис. 7.3.1).

Рис. 7.3.1.

Где — псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от к .

Модуль момента силы
(7.3.1)

где — угол между и ; — кратчайшее расстояние между линией действия силы и точкой О — плечо силы.

Моментом силы относительно неподвижной оси z называется скалярная величина равная проекции на эту ось вектора момента силы, определенного относительно произвольной точки О данной оси z (рис. 7.3.1). Значение момента , не зависит от выбора

положения точки О на оси z.

Найдем выражение для работы при вращении тела (рис. 7.3.2). Пусть сила приложена в точке В, находящейся от оси z на расстоянии , а — угол между направлением силы и радиусом-вектором . Так как тело абсолютно твердое, то работа этой силы равна работе, затраченной на поворот всего тела. При повороте тела на бесконечно малый угол точка приложения В проходит путь и работа равна произведению проекции силы на направление смещения на величину смещения:



Учитывая (7.3.1)



Получим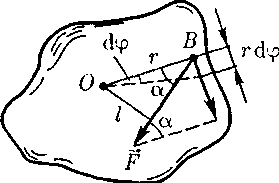



Рис. 7.3.2

Работа при вращении тела идет на увеличение его кинетической энергии: 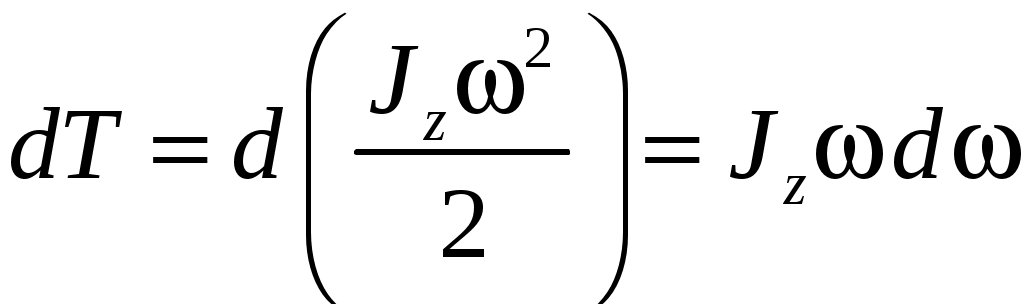, кинетическ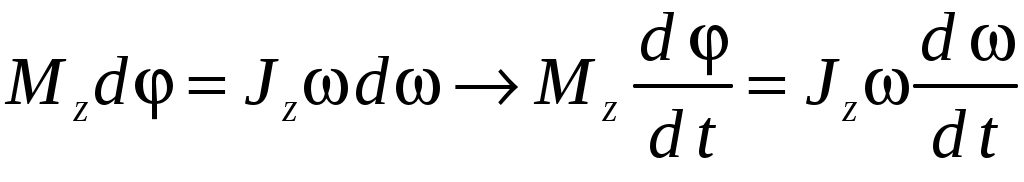ая энергия вращающегося тела

, тогда .

Учитывая, что 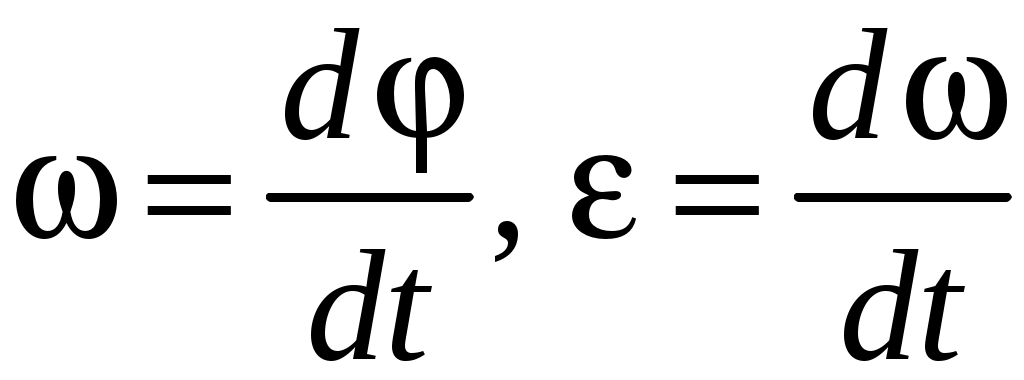получим

(7.3.2)

Уравнение (7.3.2) представляет собой уравнение динамики вращательного движения твердого тела относительно неподвижной оси.


7.4. Закон сохранения момента импульса
Моментом импульса (количества движения) материальной точки А относительно неподвижной точки О называется физическая величина, определяемая векторным произведением:



где 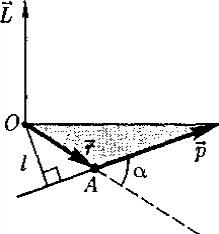— радиус-вектор, проведенный из точки О в точку А; — импульс материальной точки (рис. 7.4.1); направление вектора —совпадает с направлением поступательного движения правого винта при его вращении от к .

Рис. 7.4.1

Модуль вектора момента импульса



где — угол между векторами и ; —плечо вектора относительно точки О.

Моментом импульса относительно неподвижной оси z называется скалярная величина , равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки О данной оси. Момент импульса не зависит от положения точки О на оси z.

Момент импульса твердого тела относительно оси есть сумма моментов импульса отдельных частиц:



Используя формулу 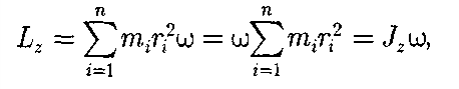получим



т.е.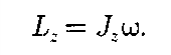

(7.4.1)

Таким образом, момент импульса твердого тела относительно оси равен произведению момента инерции тела относительно той же оси на угловую скорость.

Продифференцируем (7.4.1)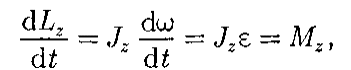



т.е.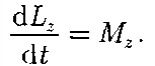



Это выражение — еще одна форма уравнения динамики вращательного движения твердого тела относительно неподвижной оси: производная момента импульса твердого тела относительно оси равна моменту сил относительно той же оси.

Можно показать, что имеет место векторное равенство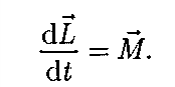

.

Если , то
(7.4.2)
Выражение (7.4.2) представляет собой закон сохранения момента импульса: момент импульса замкнутой системы сохраняется, т.е. не изменяется с течением времени.

Закон сохранения момента импульса — фундаментальный закон природы. Он связан со свойством симметрии пространства — его изотропностью, т. е. с инвариантностью физических законов относительно выбора направления осей координат системы отсчета (относительно поворота замкнутой системы в пространстве на любой угол).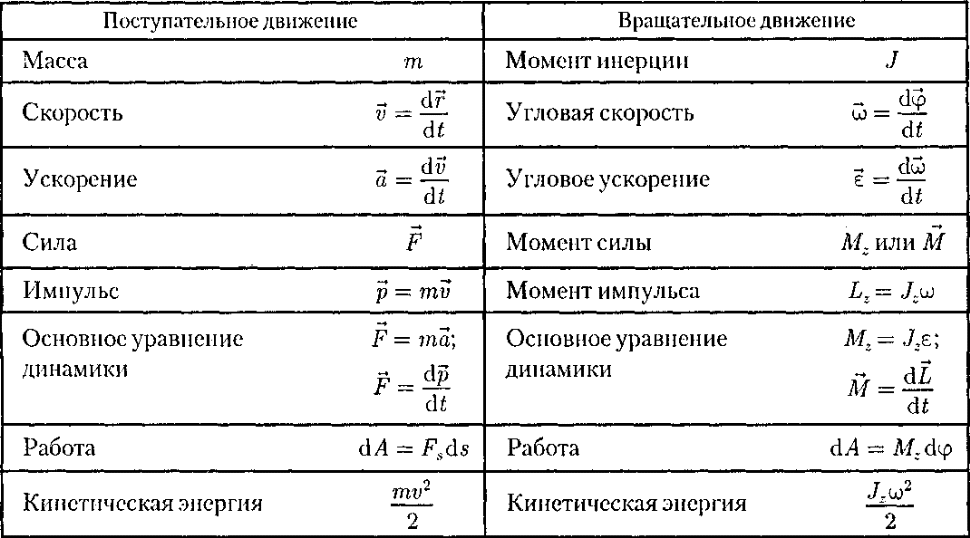