Задание 1
Задача 1
Э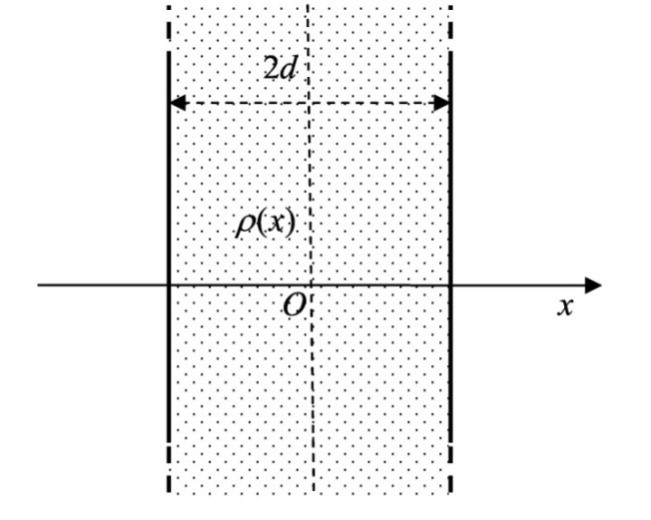 лектрический заряд распределен в пространственном слое между двумя параллельными бесконечными плоскостями симметрично относительно центральной плоскости x=0 с объемной плотностью заряда лектрический заряд распределен в пространственном слое между двумя параллельными бесконечными плоскостями симметрично относительно центральной плоскости x=0 с объемной плотностью заряда
𝑥𝑥 2
𝜌𝜌(𝑥𝑥)=𝜌𝜌01−𝑑𝑑 , зависящей от координаты x точки. Ось X перпендикулярна слою. Толщина слоя
2d. Найти с помощью теоремы Гаусса
зависимость проекции Ex на ось X вектора напряженности электрического поля от координаты точки x. Построить график этой зависимости Ex(x) в интервале изменения координаты x от –2d до 2d.
№ вар.
|
ρ0, d
|
№ вар.
|
ρ0, d
|
1
|
ρ0 = 1 нКл/м3, d= 10 см
|
11
|
ρ0 = 3нКл/м3, d= 10 см
|
2
|
ρ0 = 1 нКл/м3, d= 20 см
|
12
|
ρ0 = 3нКл/м3, d= 20 см
|
3
|
ρ0 = 1 нКл/м3, d= 30 см
|
13
|
ρ0 = 3нКл/м3, d= 30 см
|
4
|
ρ0 = 1 нКл/м3, d= 40 см
|
14
|
ρ0 = 3нКл/м3, d= 40 см
|
5
|
ρ0 = 1 нКл/м3, d= 50 см
|
15
|
ρ0 = 3нКл/м3, d= 50 см
|
6
|
ρ0 = 2нКл/м3, d= 10 см
|
16
|
ρ0 = 5нКл/м3, d= 10 см
|
7
|
ρ0 = 2нКл/м3, d= 20 см
|
17
|
ρ0 = 5нКл/м3, d= 20 см
|
№ вар.
|
ρ0, d
|
№ вар.
|
ρ0, d
|
8
|
ρ0 = 2нКл/м3, d= 30 см
|
18
|
ρ0 = 5нКл/м3, d= 30 см
|
9
|
ρ0 = 2нКл/м3, d= 40 см
|
19
|
ρ0 = 5нКл/м3, d= 40 см
|
10
|
ρ0 = 2нКл/м3, d= 50 см
|
20
|
ρ0 = 5нКл/м3, d= 50 см
|
Задача 2
Н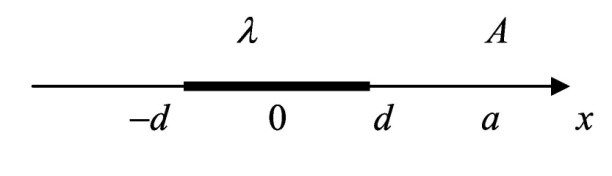 айти потенциал электростатического поля, создаваемого отрезком прямой длиной 2d в точке A. Отрезок равномерно заряжен с линейной плотностью заряда λ. Точка A лежит на оси X,направленной вдоль отрезка, на расстоянии a от его середины. айти потенциал электростатического поля, создаваемого отрезком прямой длиной 2d в точке A. Отрезок равномерно заряжен с линейной плотностью заряда λ. Точка A лежит на оси X,направленной вдоль отрезка, на расстоянии a от его середины.
№ вар.
|
a, d, λ
|
№ вар.
|
a, d, λ
|
1
|
a = 5 см, d = 1 см, λ = 12 нКл/м
|
11
|
a = 5 см, d = 1 см, λ = 22 нКл/м
|
2
|
a = 8 см, d = 2 см, λ = 10 нКл/м
|
12
|
a = 8 см, d = 2 см, λ = 20 нКл/м
|
3
|
a = 5 см, d = 2 см, λ = 14 нКл/м
|
13
|
a = 5 см, d = 2 см, λ = 24 нКл/м
|
4
|
a = 7 см, d = 1 см, λ = 18 нКл/м
|
14
|
a = 7 см, d = 1 см, λ = 28 нКл/м
|
5
|
a = 5 см, d = 3 см, λ = 2 нКл/м
|
15
|
a = 5 см, d = 3 см, λ = 22 нКл/м
|
6
|
a = 15 см, d = 10 см, λ = 12 нКл/м
|
16
|
a = 15 см, d = 10 см, λ = 32 нКл/м
|
7
|
a = 7 см, d = 2 см, λ = 11 нКл/м
|
17
|
a = 7 см, d = 2 см, λ = 31 нКл/м
|
8
|
a = 5 см, d = 4 см, λ = 10 нКл/м
|
18
|
a = 5 см, d = 4 см, λ = 30 нКл/м
|
№ вар.
|
a, d, λ
|
№ вар.
|
a, d, λ
|
9
|
a = 9 см, d = 3 см, λ = 20 нКл/м
|
19
|
a = 9 см, d = 3 см, λ = 30 нКл/м
|
10
|
a = 5 см, d = 1 см, λ = 15 нКл/м
|
20
|
a = 5 см, d = 1 см, λ = 25 нКл/м
|
З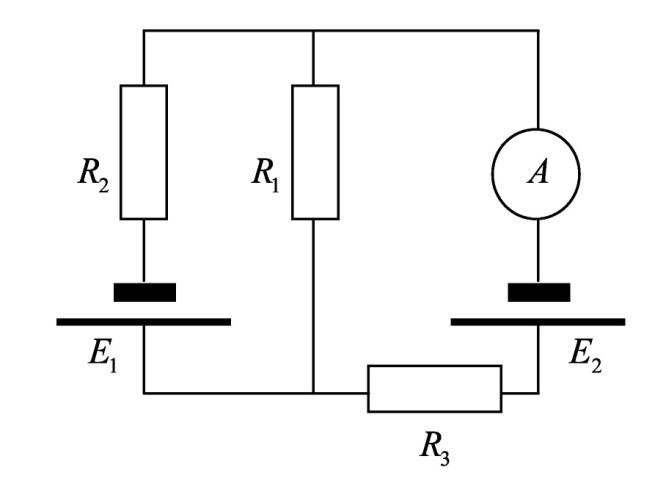 адача 3 адача 3
№ вар.
|
RA
|
№ вар.
|
RA
|
1
|
RA = 0,10 Ом
|
11
|
RA = 0,15 Ом
|
2
|
RA = 0,20 Ом
|
12
|
RA = 0,25 Ом
|
3
|
RA = 0,30 Ом
|
13
|
RA = 0,35 Ом
|
4
|
RA = 0,40 Ом
|
14
|
RA = 0,45 Ом
|
5
|
RA = 0,50 Ом
|
15
|
RA = 0,55 Ом
|
6
|
RA = 0,60 Ом
|
16
|
RA = 0,65 Ом
|
В схеме, приведенной на рисунке, ЭДС источников E1 = 2 В, E2 = 3 В, сопротивления резисторов R1 = 0,2 Ом, R2 = 1 Ом, R3 = 0,5 Ом, сопротивление амперметра равно RA. Найти показание амперметра. Внутренним сопротивлением источников пренебречь.
№ вар.
|
RA
|
№ вар.
|
RA
|
7
|
RA = 0,70 Ом
|
17
|
RA = 0,75 Ом
|
8
|
RA = 0,80 Ом
|
18
|
RA = 0,85 Ом
|
9
|
RA = 0,90 Ом
|
19
|
RA = 0,95 Ом
|
10
|
RA = 1,00 Ом
|
20
|
RA = 1,05 Ом
|
Задание 2
Задача 1
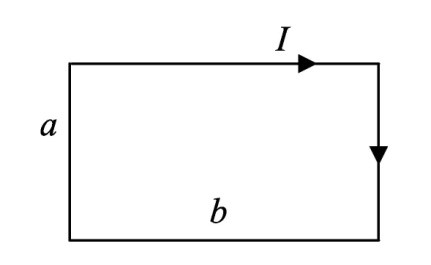
Найти индукцию магнитного поля в центре прямоугольного проводящего контура со сторонами a и b, по которому течет ток силой I.
№ вар.
|
I, a, b
|
№ вар.
|
I, a, b
|
1
|
I = 2 А a, =10 см b, = 6 см
|
11
|
I = 5 А a, =10 см b, = 6 см
|
2
|
I = 2 А a, =12 см b, = 6 см
|
12
|
I = 5 А a, =12 см b, = 6 см
|
3
|
I = 2 А a, =10 см b, = 4 см
|
13
|
I = 5 А a, =10 см b, = 4 см
|
4
|
I = 2 А a, =8 см b, = 6 см
|
14
|
I = 5 А a, =8 см b, = 6 см
|
5
|
I = 2 А a, = 6 см b, = 4 см
|
15
|
I = 5 А a, = 6 см b, = 4 см
|
6
|
I = 2 А a, =14 см b, =16 см
|
16
|
I = 5 А a, =14 см b, =16 см
|
7
|
I = 2 А a, =18 см b, = 6 см
|
17
|
I = 5 А a, =18 см b, = 6 см
|
8
|
I = 2 А a, =10 см b, =16 см
|
18
|
I = 5 А a, =10 см b, =16 см
|
9
|
I = 2 А a, = 2 см b, = 6 см
|
19
|
I = 5 А a, = 2 см b, = 6 см
|
10
|
I = 2 А a, = 5 см b, = 7 см
|
20
|
I = 5 А a, = 5 см b, = 7 см
|
Задача 2
Н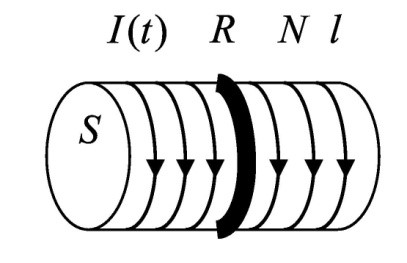 а соленоид длиной l = 10 см и площадью поперечного сечения S= 5 см2 надет проволочный виток а соленоид длиной l = 10 см и площадью поперечного сечения S= 5 см2 надет проволочный виток
сопротивлением R = 1 Ом. Обмотка соленоида имеет N = 500 витков, и по нему идет ток, сила которого меняется со временем по заданному закону 𝐼𝐼(𝑡𝑡)= 𝐼𝐼01−𝑒𝑒−𝑡𝑡/𝜏𝜏. Найти зависимость от времени силы тока
I1(t) в проволочном витке и построить график этой зависимости в интервале времени от 0до t.
№ вар.
|
I0, τ, t
|
№ вар.
|
I0, τ, t
|
1
|
I0 = 1 А, τ = 1 с, t = 0,5 с
|
11
|
I0 = 2А, τ = 1 с, t = 0,5 с
|
2
|
I0 = 1 А, τ = 1 с, t = 1 с
|
12
|
I0 = 2А, τ = 1 с, t = 1 с
|
3
|
I0 = 1 А, τ = 1 с, t = 2 с
|
13
|
I0 = 2А, τ = 1 с, t = 2 с
|
4
|
I0 = 1 А, τ = 1 с, t = 3 с
|
14
|
I0 = 2А, τ = 1 с, t = 3 с
|
5
|
I0 = 1 А, τ = 1 с, t = 4 с
|
15
|
I0 = 2А, τ = 1 с, t = 4 с
|
6
|
I0 = 1 А, τ = 2 с, t = 0,5 с
|
16
|
I0 = 2А, τ = 2 с, t = 0,5 с
|
7
|
I0 = 1 А, τ = 2 с, t = 1 с
|
17
|
I0 = 2А, τ = 2 с, t = 1 с
|
8
|
I0 = 1 А, τ = 2 с, t = 2 с
|
18
|
I0 = 2А, τ = 2 с, t = 2 с
|
9
|
I0 = 1 А, τ = 2 с, t = 3 с
|
19
|
I0 = 2А, τ = 2 с, t = 3 с
|
10
|
I0 = 1 А, τ = 2 с, t = 4 с
|
20
|
I0 = 2А, τ = 2 с, t = 4 с
|
Задача 3
П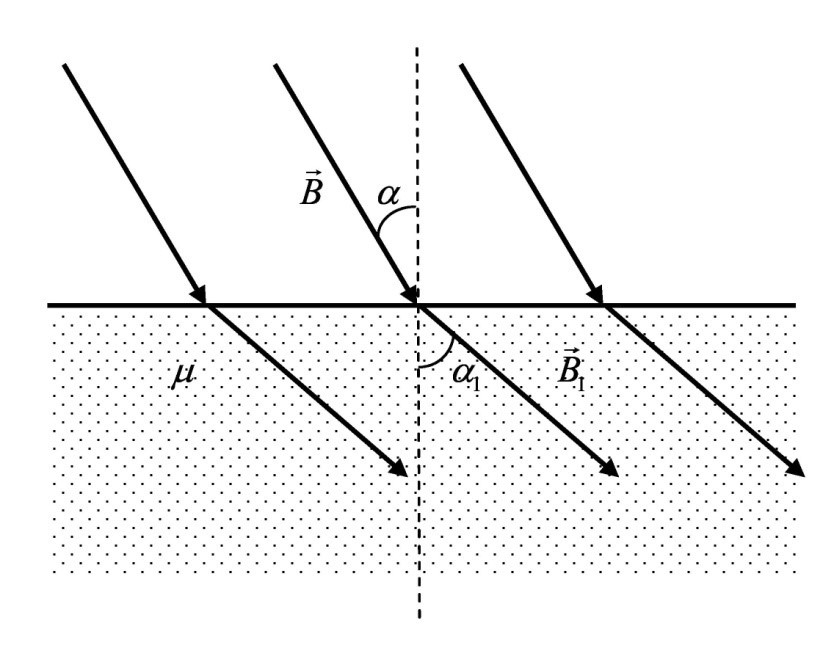 олупространство, заполненное веществом с магнитной проницаемостью μ, отделено от вакуума бесконечной плоскостью. В вакууме имеется однородное магнитное поле с индукцией B, направление которого составляет угол α с нормалью к поверхности раздела. Найти модуль индукции B1 магнитного поля в веществе и угол α1 между вектором индукции магнитного поля в веществе и нормалью к поверхности раздела. олупространство, заполненное веществом с магнитной проницаемостью μ, отделено от вакуума бесконечной плоскостью. В вакууме имеется однородное магнитное поле с индукцией B, направление которого составляет угол α с нормалью к поверхности раздела. Найти модуль индукции B1 магнитного поля в веществе и угол α1 между вектором индукции магнитного поля в веществе и нормалью к поверхности раздела.
№ вар.
|
B,α, μ
|
№ вар.
|
B,α, μ
|
1
|
B = 1мТл,α= 10º, μ = 10
|
11
|
B = 1мТл,α= 10º, μ = 15
|
2
|
B = 1мТл,α= 15º, μ = 10
|
12
|
B = 1мТл,α= 15º, μ = 15
|
3
|
B = 1мТл,α= 20º, μ = 10
|
13
|
B = 1 мТл,α= 20º, μ = 15
|
4
|
B = 1мТл,α= 25º, μ = 10
|
14
|
B = 1 мТл,α= 25º, μ = 15
|
5
|
B = 1мТл,α= 30º, μ = 10
|
15
|
B = 1 мТл,α= 30º, μ = 15
|
6
|
B = 1мТл,α= 10º, μ = 5
|
16
|
B = 1 мТл,α= 11º, μ = 20
|
№ вар.
|
B,α, μ
|
№ вар.
|
B,α, μ
|
7
|
B = 1мТл,α= 15º, μ = 5
|
17
|
B = 1 мТл,α= 12º, μ = 20
|
8
|
B = 1мТл,α= 20º, μ = 5
|
18
|
B = 1 мТл,α= 13º, μ = 20
|
9
|
B = 1мТл,α= 25º, μ = 5
|
19
|
B = 1 мТл,α= 14º, μ = 20
|
10
|
B = 1мТл,α= 30º, μ = 5
|
20
|
B = 1 мТл,α= 15º, μ = 20
| |
 Скачать 243.77 Kb.
Скачать 243.77 Kb. лектрический заряд распределен в пространственном слое между двумя параллельными бесконечными плоскостями симметрично относительно центральной плоскости x=0 с объемной плотностью заряда
лектрический заряд распределен в пространственном слое между двумя параллельными бесконечными плоскостями симметрично относительно центральной плоскости x=0 с объемной плотностью заряда 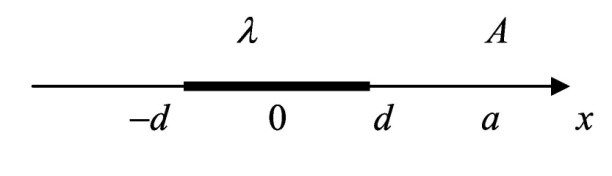 айти потенциал электростатического поля, создаваемого отрезком прямой длиной 2d в точке A. Отрезок равномерно заряжен с линейной плотностью заряда λ. Точка A лежит на оси X,направленной вдоль отрезка, на расстоянии a от его середины.
айти потенциал электростатического поля, создаваемого отрезком прямой длиной 2d в точке A. Отрезок равномерно заряжен с линейной плотностью заряда λ. Точка A лежит на оси X,направленной вдоль отрезка, на расстоянии a от его середины.  адача 3
адача 3 
 а соленоид длиной l = 10 см и площадью поперечного сечения S= 5 см2 надет проволочный виток
а соленоид длиной l = 10 см и площадью поперечного сечения S= 5 см2 надет проволочный виток  олупространство, заполненное веществом с магнитной проницаемостью μ, отделено от вакуума бесконечной плоскостью. В вакууме имеется однородное магнитное поле с индукцией B, направление которого составляет угол α с нормалью к поверхности раздела. Найти модуль индукции B1 магнитного поля в веществе и угол α1 между вектором индукции магнитного поля в веществе и нормалью к поверхности раздела.
олупространство, заполненное веществом с магнитной проницаемостью μ, отделено от вакуума бесконечной плоскостью. В вакууме имеется однородное магнитное поле с индукцией B, направление которого составляет угол α с нормалью к поверхности раздела. Найти модуль индукции B1 магнитного поля в веществе и угол α1 между вектором индукции магнитного поля в веществе и нормалью к поверхности раздела. 