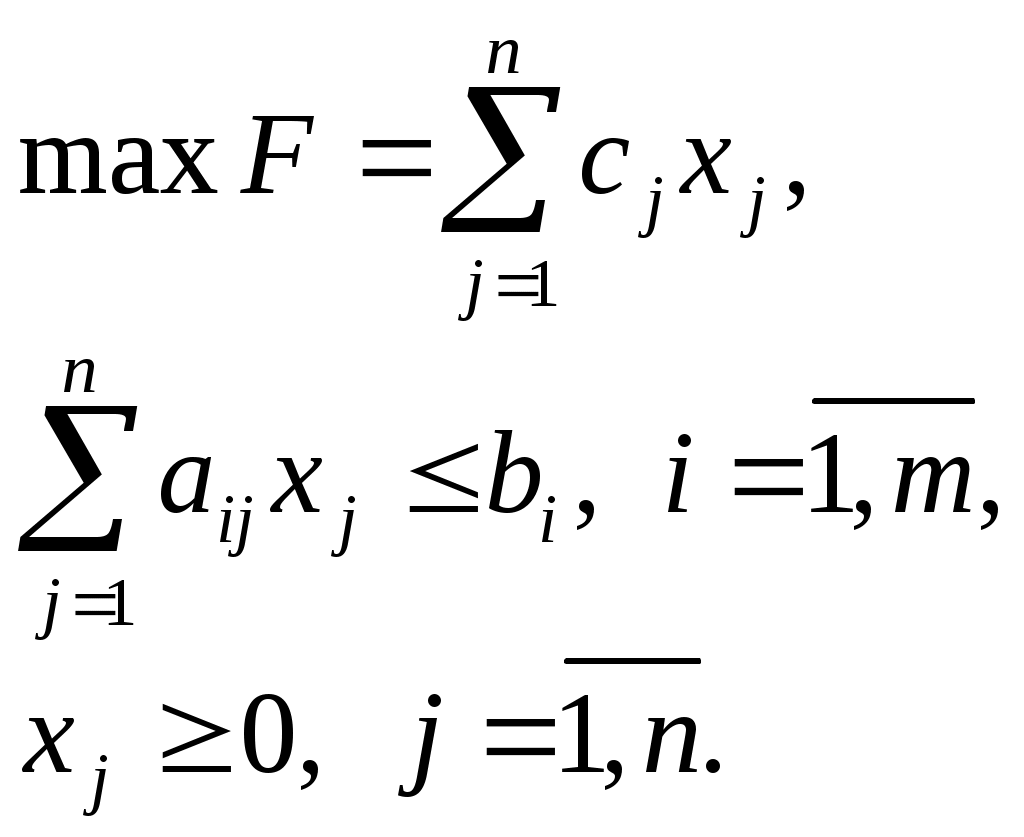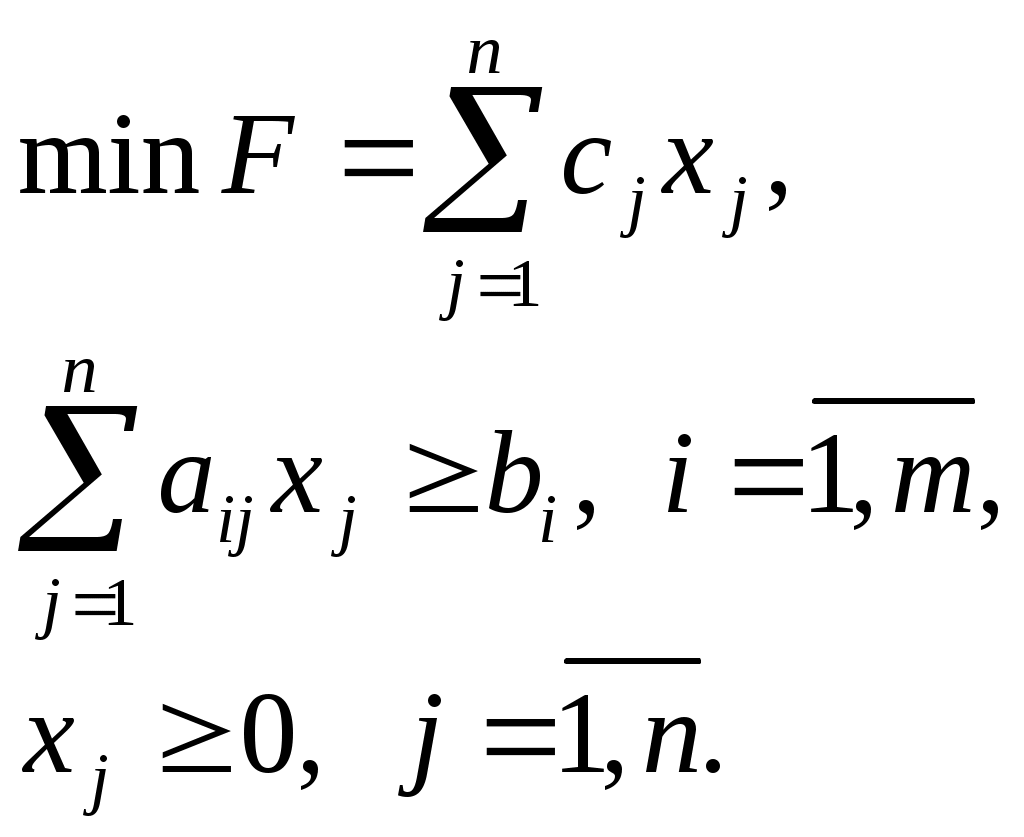|
|
Примеры экономических задач ЛП. 1. 1 Примеры экономических задач (ЛП) лп
1.1 Примеры экономических задач (ЛП)
 ЛП – раздел МП, в котором разрабатываются методы отыскания экстремума линейных функций многих переменных при линейных дополнительных ограничениях, налагаемых на эти переменные. ЛП – раздел МП, в котором разрабатываются методы отыскания экстремума линейных функций многих переменных при линейных дополнительных ограничениях, налагаемых на эти переменные.
Задача о наилучшем использовании ресурсов. Пусть некоторая производственная единица производит n видов продукции, при этом используется m видов ресурсов. Известны следующие параметры: 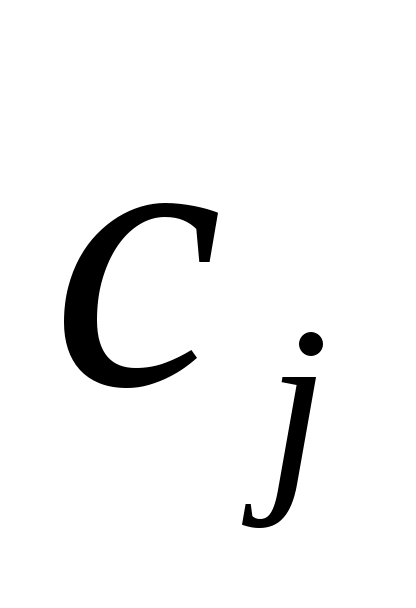 , , 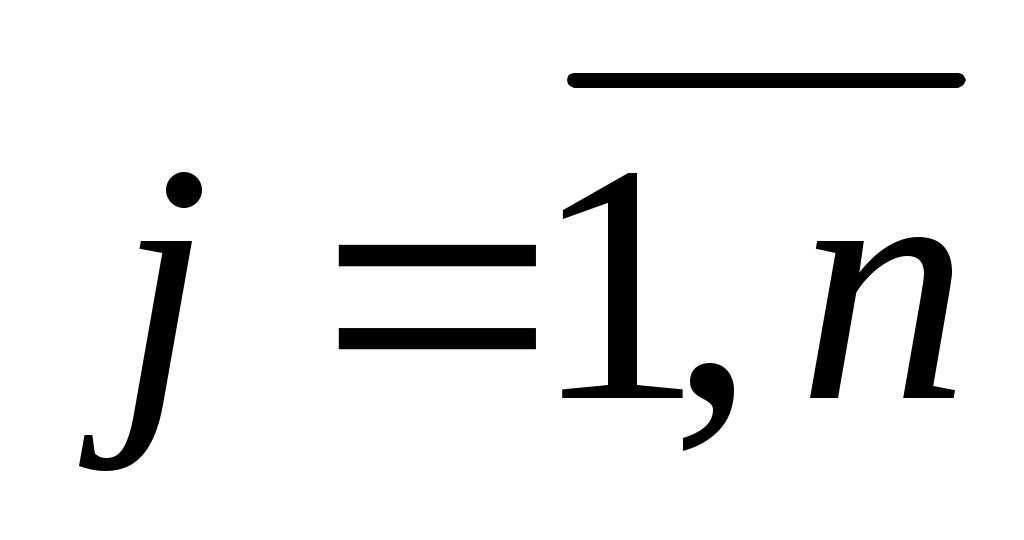 – цена единицы продукции j–го вида; – цена единицы продукции j–го вида; 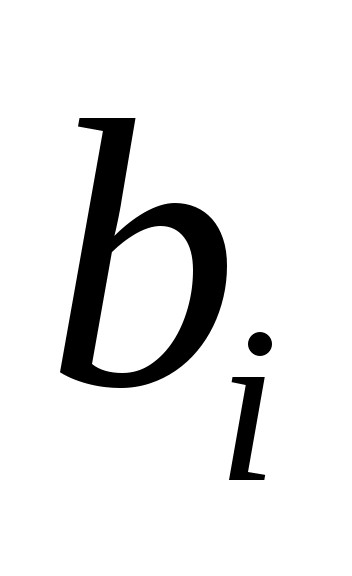 , , 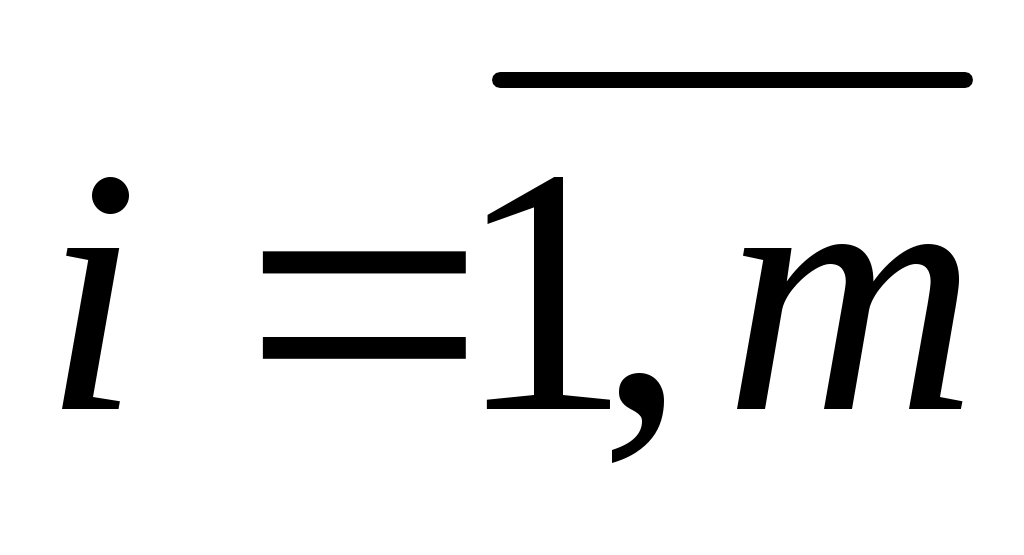 – количество i–го ресурса; – количество i–го ресурса;  , , 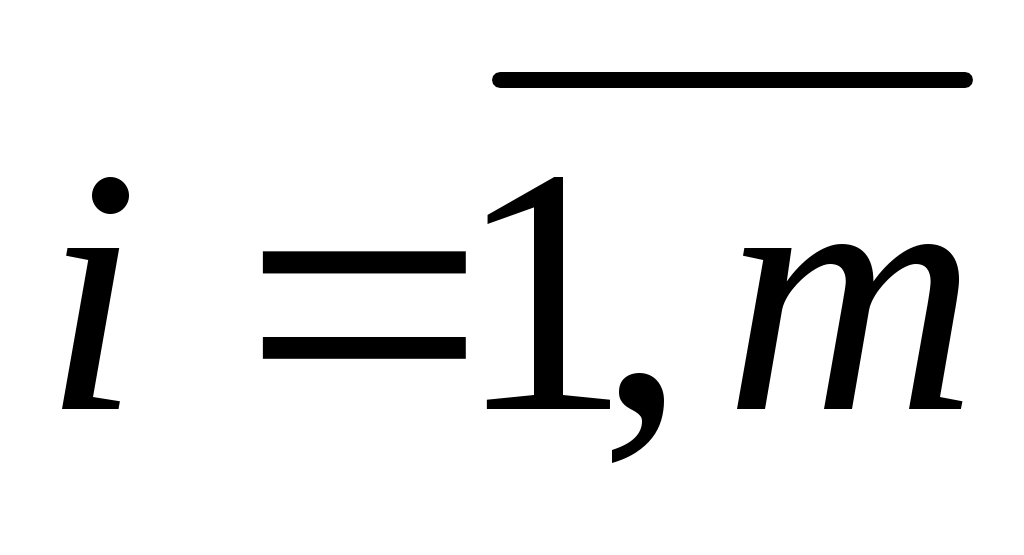 , , 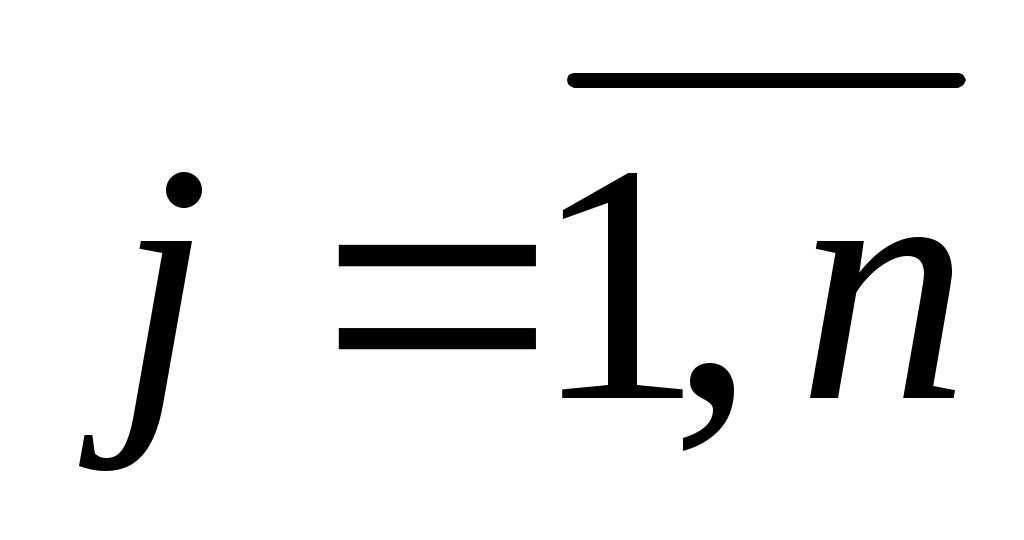 – количество i–го ресурса для производства единицы продукции j–го вида. – количество i–го ресурса для производства единицы продукции j–го вида.
Требуется определить план производства 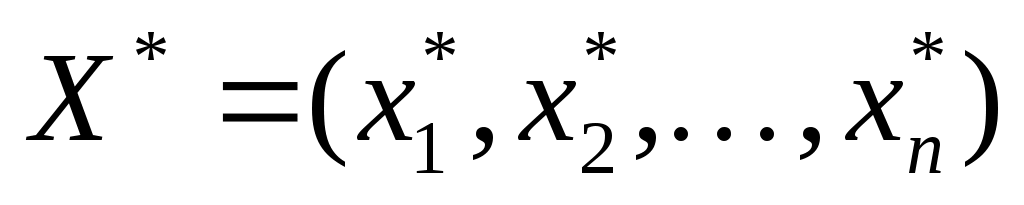 , т.е. планируемый объем производства каждого вида продукции, при котором обеспечивается максимальная прибыль при имеющихся ресурсах. , т.е. планируемый объем производства каждого вида продукции, при котором обеспечивается максимальная прибыль при имеющихся ресурсах.
Так как 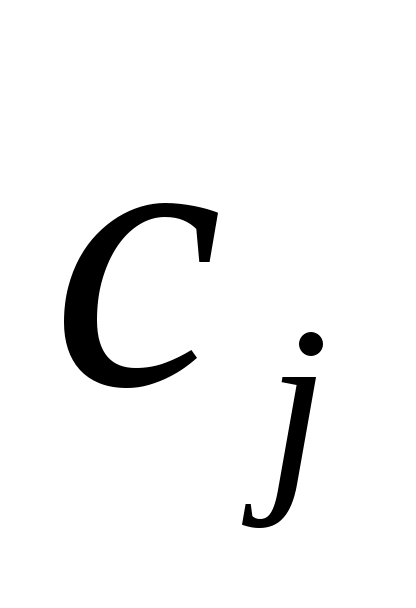 – цена единицы продукции j–го вида, то цена – цена единицы продукции j–го вида, то цена 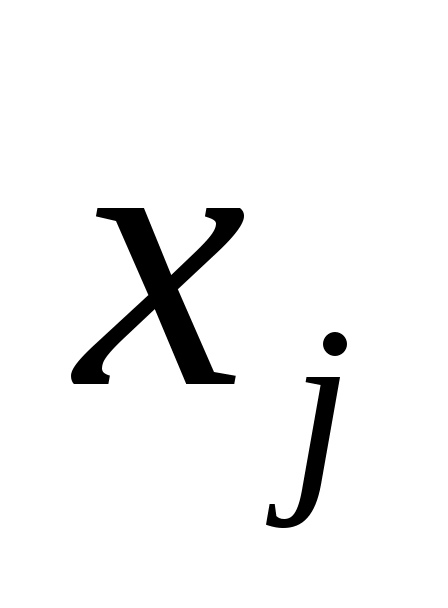 единиц будет равна единиц будет равна 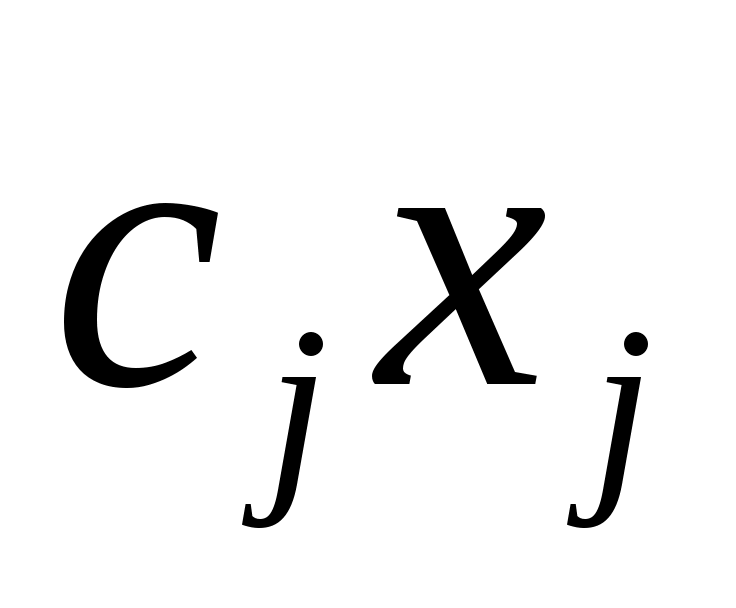 , а общий объем реализации составит , а общий объем реализации составит
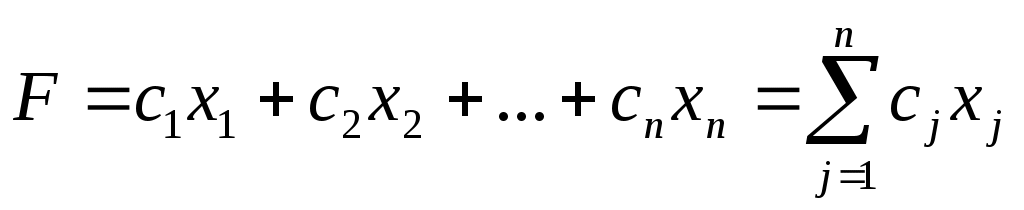 . .
Так как  – расход i–го ресурса на производство единицы продукции j–го вида, тогда расход этого ресурса на производство – расход i–го ресурса на производство единицы продукции j–го вида, тогда расход этого ресурса на производство 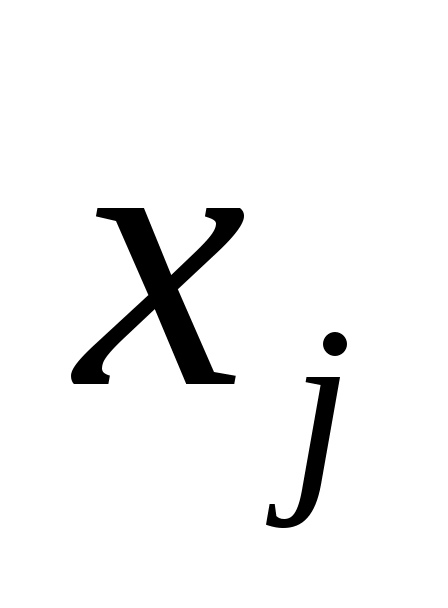 единиц будет равен единиц будет равен 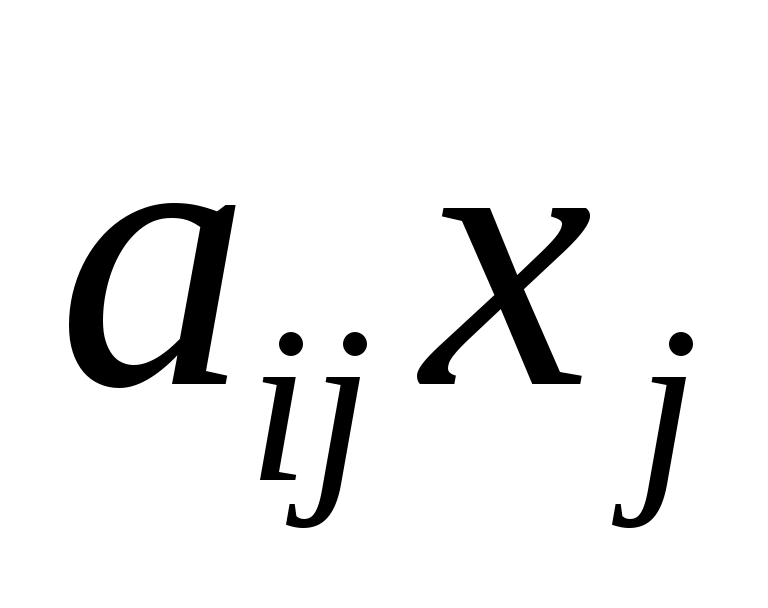 , а расход i–го ресурса на выпуск всех n видов продукции, который не должен превышать , а расход i–го ресурса на выпуск всех n видов продукции, который не должен превышать 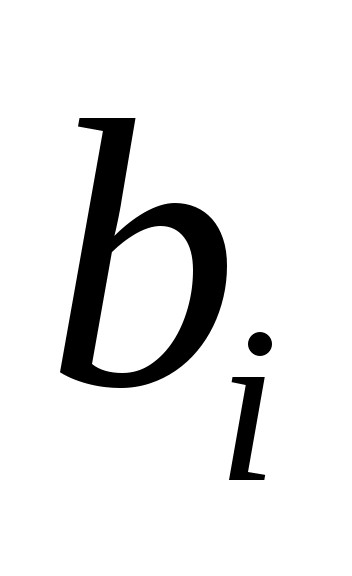 , составит , составит
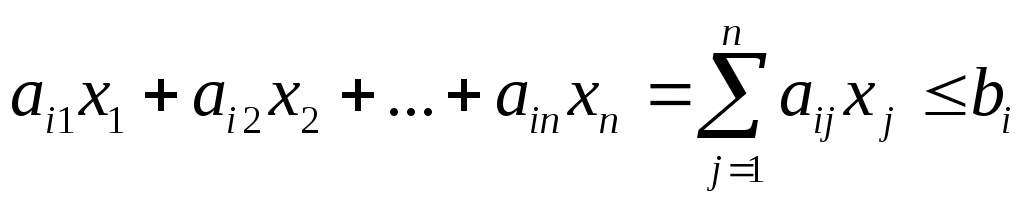 , , 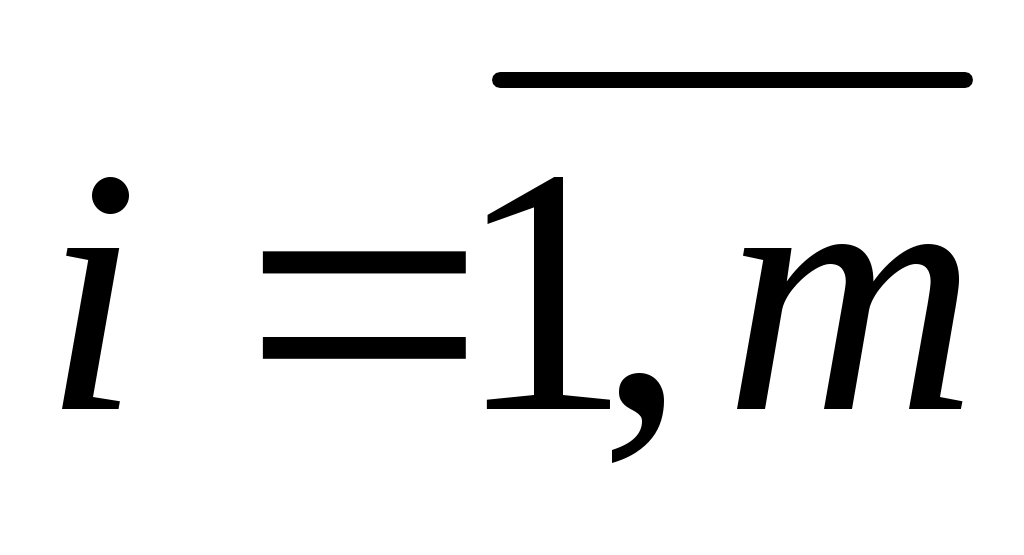 . .
Чтобы искомый план был реален, наряду с ограничениями на ресурсы, нужно на объемы выпуска продукции наложить условие неотрицательности 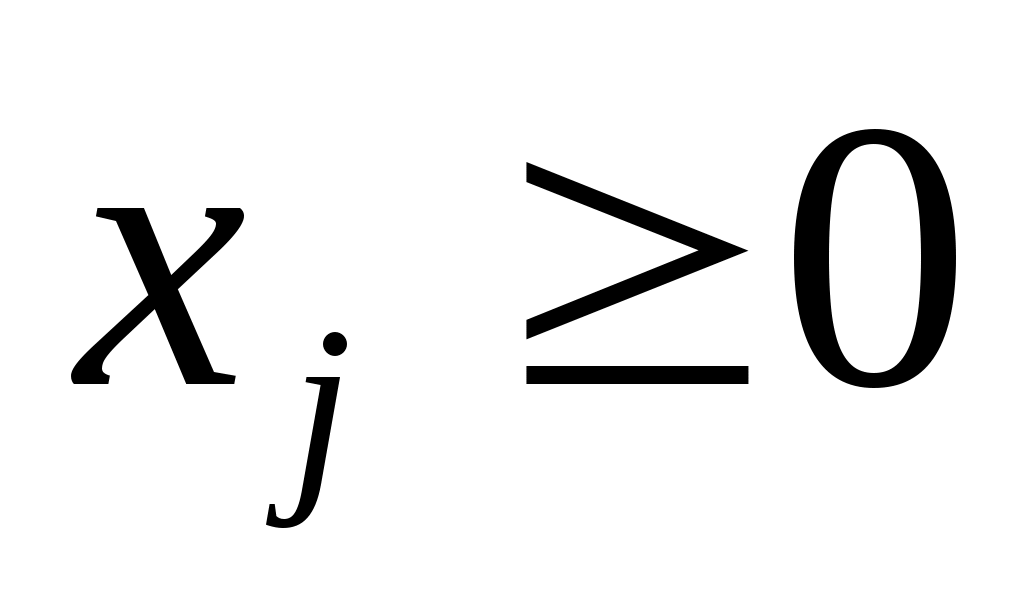 , , 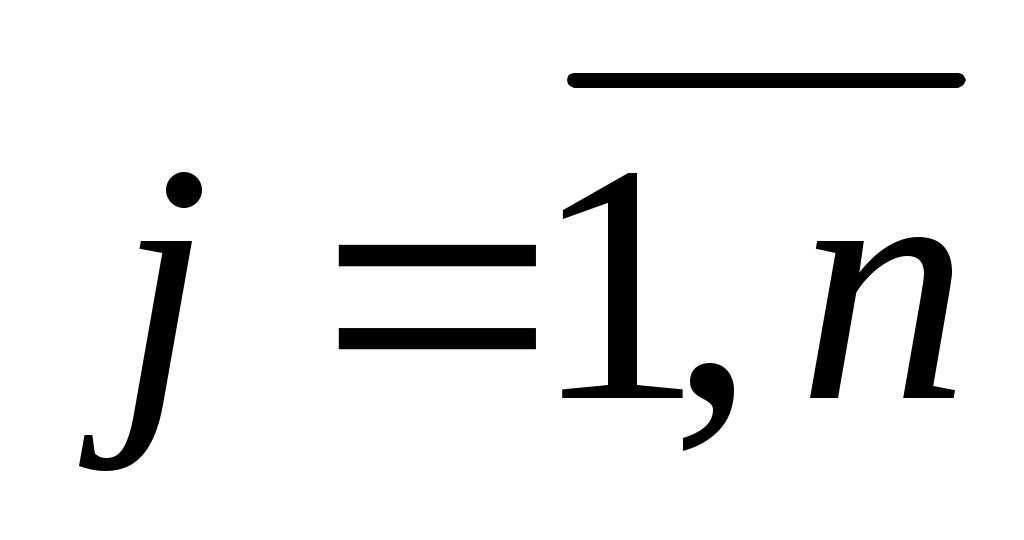 . .
Таким образом, ЭММ о наилучшем использовании ресурсов примет вид:
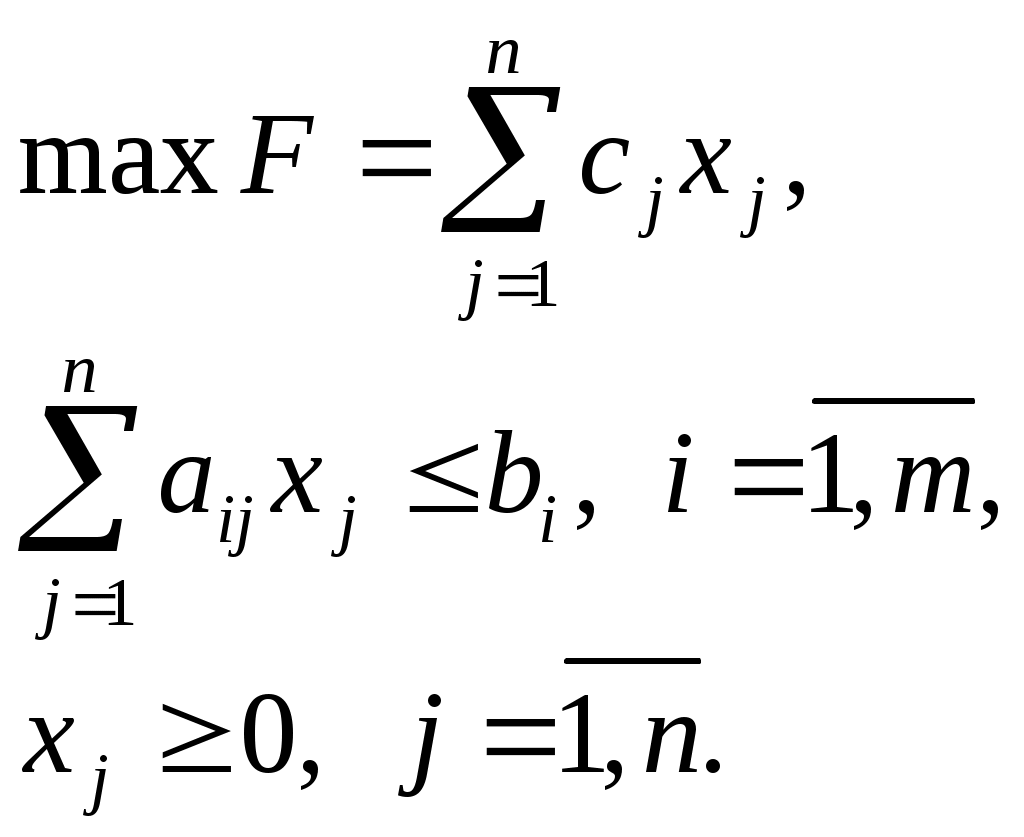
Задача о диете (о рационе). Пусть имеется n продуктов питания, в которых содержится m полезных веществ. Известны следующие параметры: 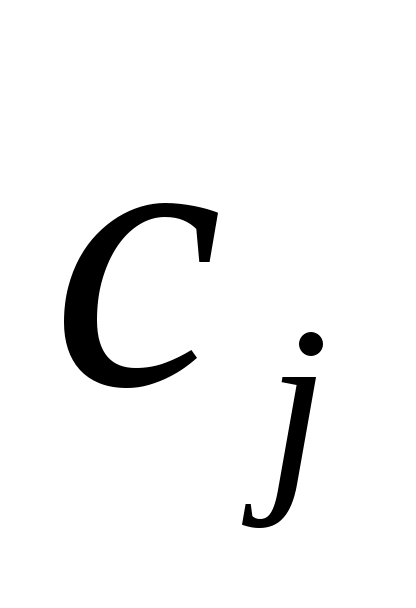 , , 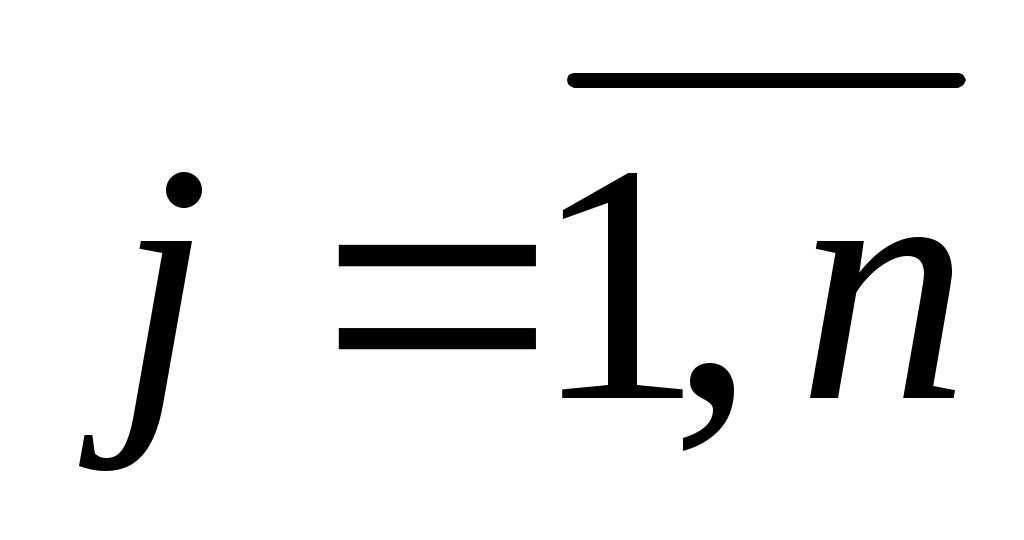 – цена единицы j–го продукта; – цена единицы j–го продукта; 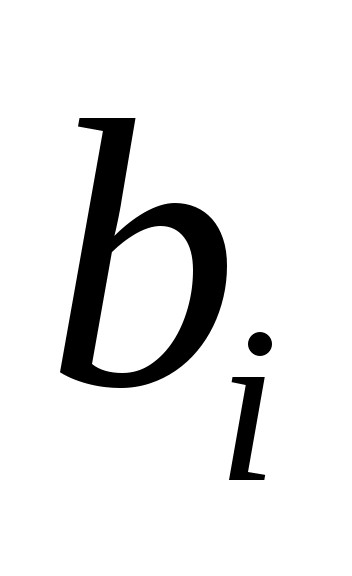 , , 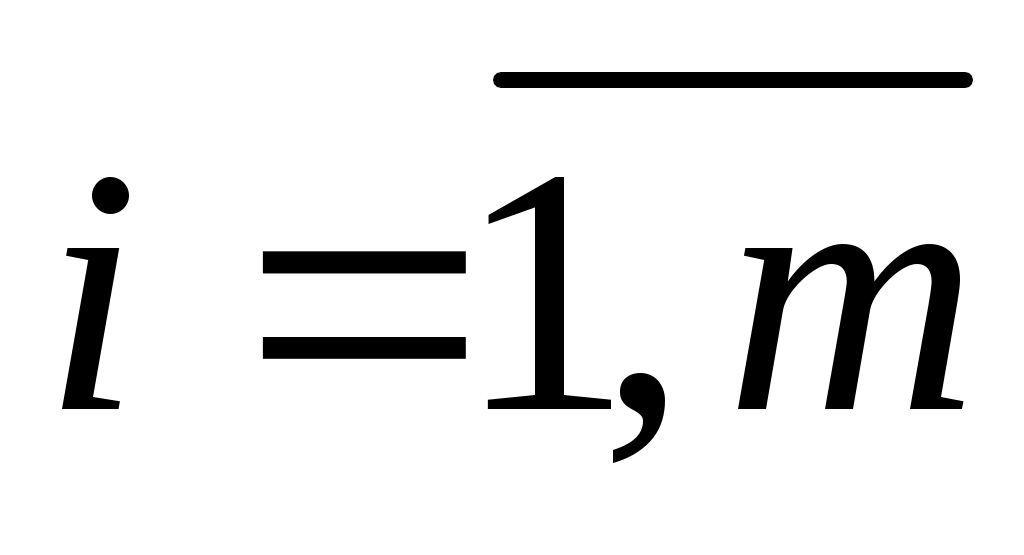 – минимальное количество i–го полезного вещества, которое должно потребляться за определенный промежуток времени; – минимальное количество i–го полезного вещества, которое должно потребляться за определенный промежуток времени;  , , 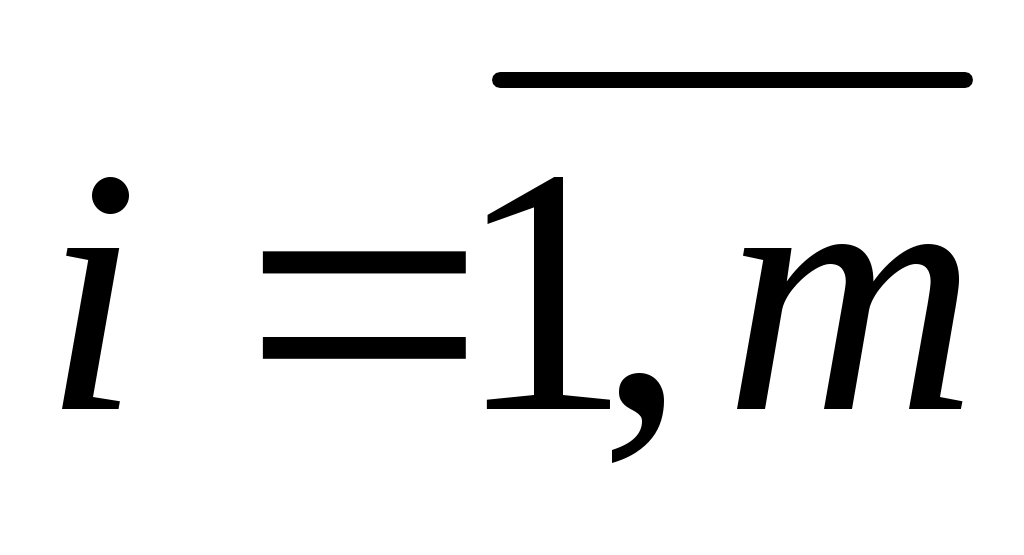 , , 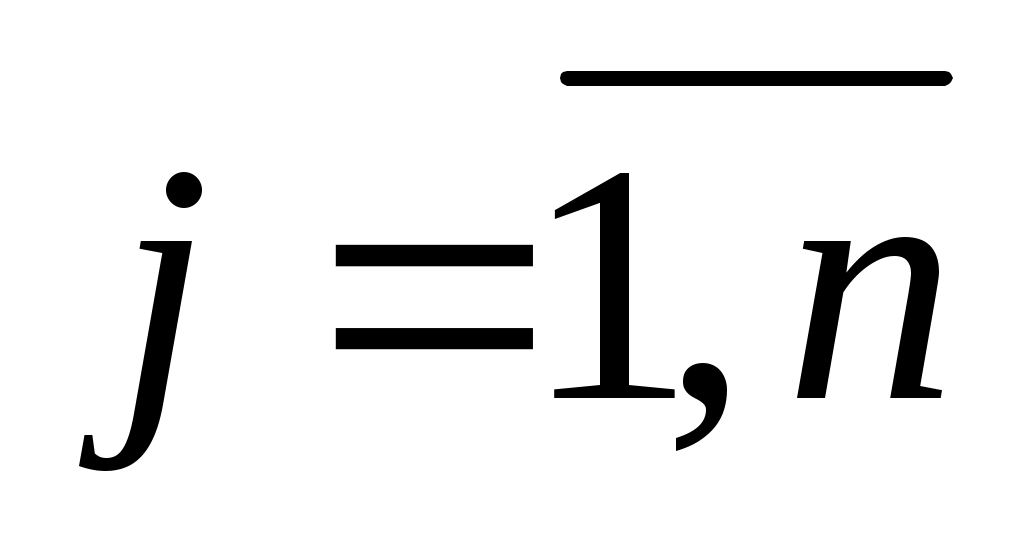 – содержание i–го полезного вещества в единице j–го продукта. – содержание i–го полезного вещества в единице j–го продукта.
Требуется определить количество приобретения продуктов каждого вида 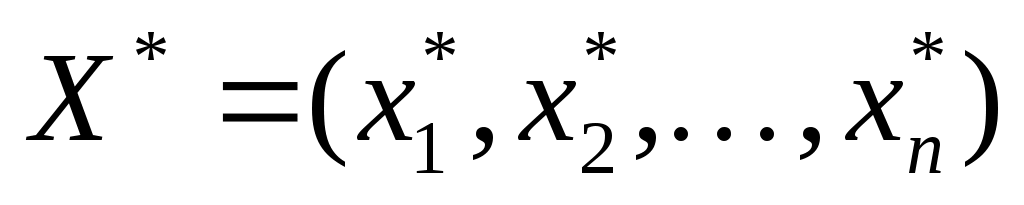 , обеспечивающие необходимое количество полезных веществ при минимальной стоимости продуктов питания. , обеспечивающие необходимое количество полезных веществ при минимальной стоимости продуктов питания.
Если 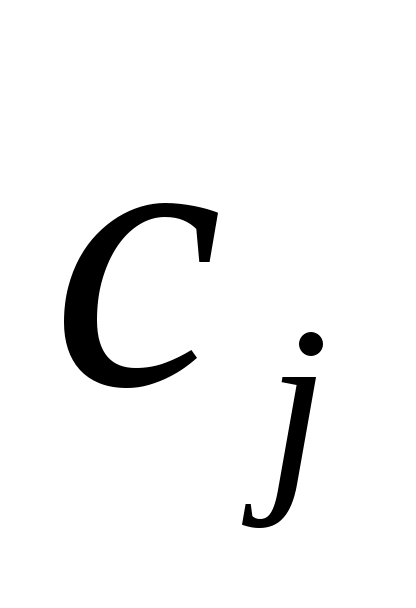 – цена единицы j–го продукта, тогда цена – цена единицы j–го продукта, тогда цена 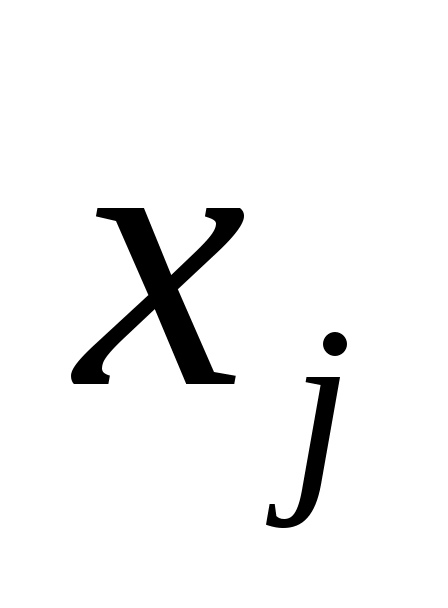 единиц будет равна единиц будет равна 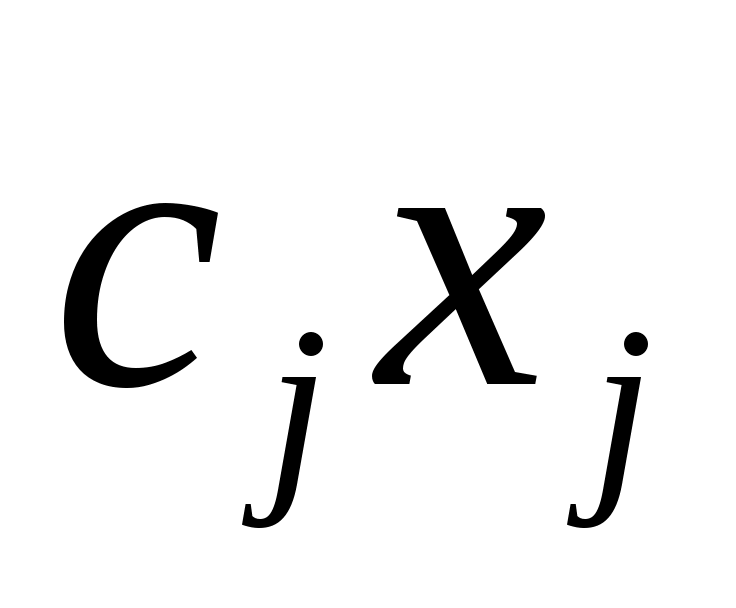 , а цена n продуктов питания составит , а цена n продуктов питания составит
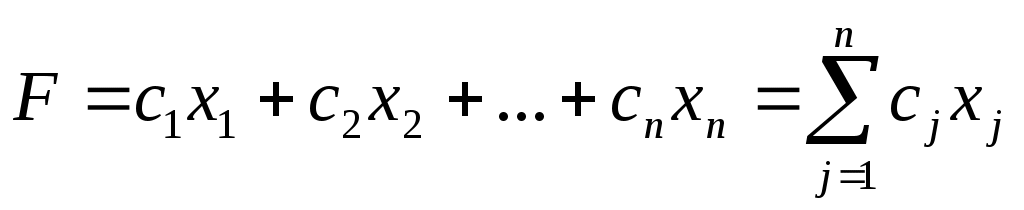 . .
Если  – содержание i–го полезного вещества в единице j–го продукта, тогда содержание i–го вещества в – содержание i–го полезного вещества в единице j–го продукта, тогда содержание i–го вещества в 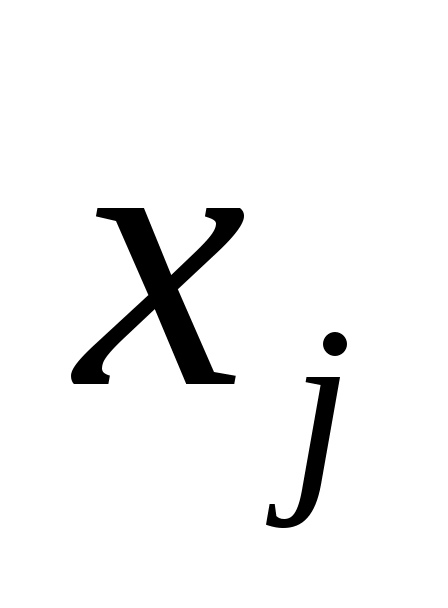 единиц этого продукта равна единиц этого продукта равна 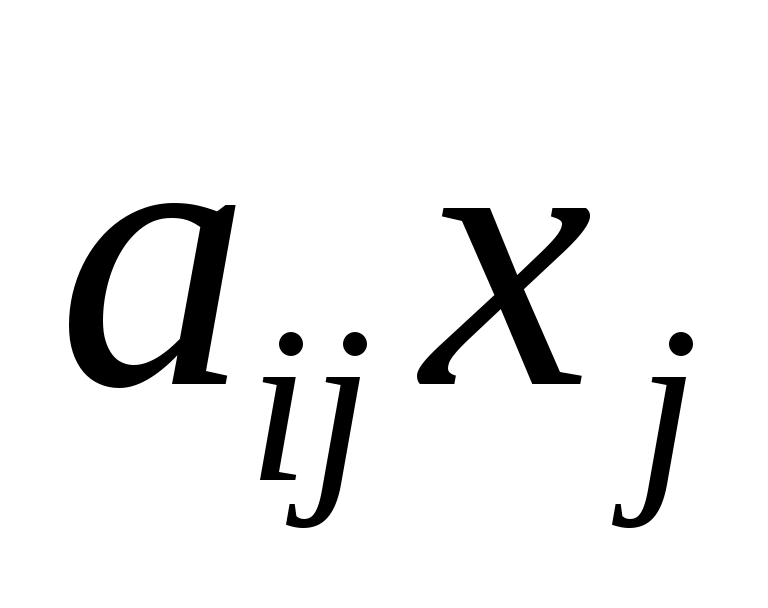 , а содержание i–го вещества в n продуктах питания, которое должно быть не меньше , а содержание i–го вещества в n продуктах питания, которое должно быть не меньше 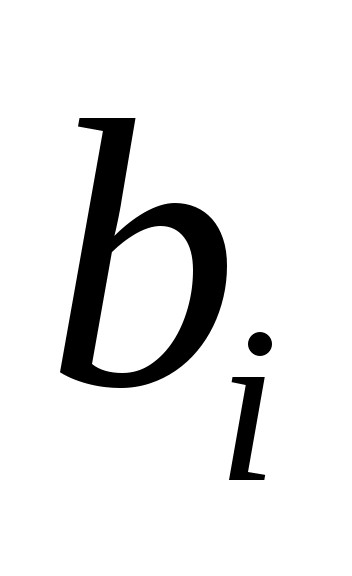 , равно , равно
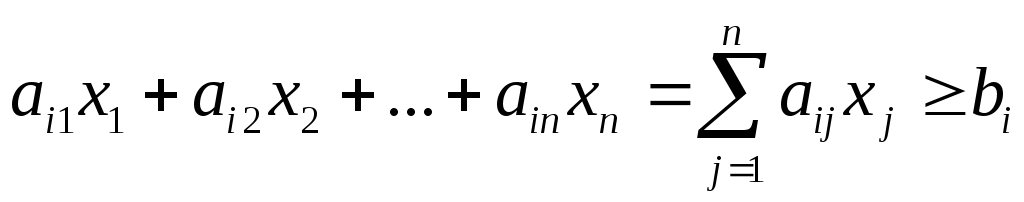 , , 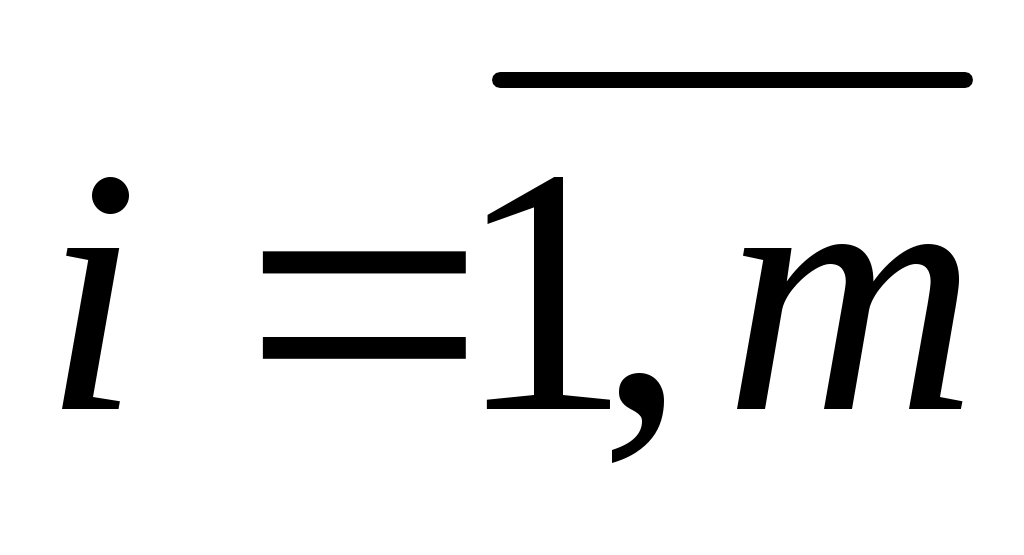 . .
ЭММ задачи о диете будет иметь вид:
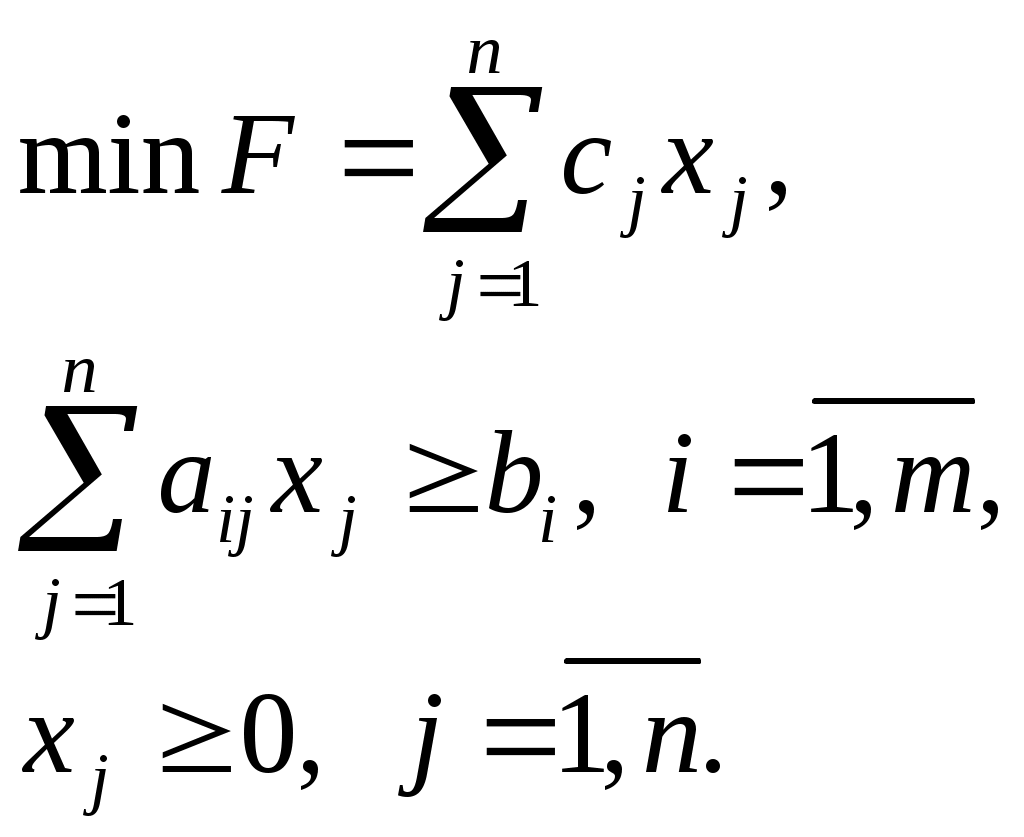
|
|
|
 Скачать 108 Kb.
Скачать 108 Kb.