Безотказность. 1. 1 Вероятность безотказной работы
 Скачать 325.83 Kb.
|
|
1.1 Вероятность безотказной работы Вероятностью безотказной работы называется вероятность того, что при определенных условиях эксплуатации, в пределах заданной наработки не произойдет ни одного отказа. Вероятность безотказной работы обозначается как P(l), которая определяется по формуле (1.1):  где N0 – число элементов в начале испытания; r(l) – число отказов элементов к моменту наработки. Следует отметить, что чем больше величина N0, тем с большей точностью можно рассчитать вероятность P(l). В начале эксплуатации исправного локомотива P(0) = 1, так как при пробеге l = 0 вероятность того, что ни один элемент не откажет, принимает максимальное значение – 1. С ростом пробега l вероятность P(l) будет уменьшаться. В процессе приближения срока эксплуатации к бесконечно большой величине вероятность безотказной работы будет стремиться к нулю P(l→∞) = 0. Таким образом в процессе наработки величина вероятности безотказной работы изменяется в пределах от 1 до 0. Характер изменения вероятности безотказной работы в функции пробега показан на рис. 1.1.  Рис.2.1. График изменения вероятности безотказной работы P(l)в зависимости от наработки Основными достоинствами использования данного показателя при расчетах является два фактора: во-первых, вероятность безотказной работы охватывает все факторы, влияющие на надежность элементов, позволяя достаточно просто судить о его надежности, т.к. чем больше величина P(l), тем выше надежность; во-вторых, вероятность безотказной работы может быть использована в расчетах надежности сложных систем, состоящих из более чем одного элемента. 1.2 Вероятность отказа Вероятностью отказа называют вероятность того, что при определенных условиях эксплуатации, в пределах заданной наработки произойдет хотя бы один отказ. Вероятность отказа обозначается как Q(l), которая определяется по формуле (1.2):  В начале эксплуатации исправного локомотива Q(0) = 0, так как при пробеге l = 0 вероятность того, что хотя бы один элемент откажет, принимает минимальное значение – 0. С ростом пробега l вероятность отказа Q(l) будет увеличиваться. В процессе приближения срока эксплуатации к бесконечно большой величине вероятность отказа будет стремиться к единице Q(l→∞) = 1. Таким образом в процессе наработки величина вероятности отказа изменяется в пределах от 0 до 1. Характер изменения вероятности отказа в функции пробега показан на рис. 1.2.Вероятность безотказной работы и вероятность отказа являются событиями противоположными и несовместимыми.  Рис.2.2. График изменения вероятности отказа Q(l) в зависимости от наработки 1.3 Частота отказов Частота отказов – это отношение числа элементов в единицу времени или пробега отнесенного к первоначальному числу испытуемых элементов. Другими словами частота отказов является показателем, характеризующим скорость изменения вероятности отказов и вероятности безотказной работы по мере роста длительности работы. Частота отказов обозначается как  и определяется по формуле (1.3): где –  количество отказавших элементов за промежуток пробега  .Данный показатель позволяет судить по его величине о числе элементов, которые откажут на каком-то промежутке времени или пробега, также по его величине можно рассчитать количество требуемых запасных частей. Характер изменения частоты отказов в функции пробега показан на рис. 1.3. 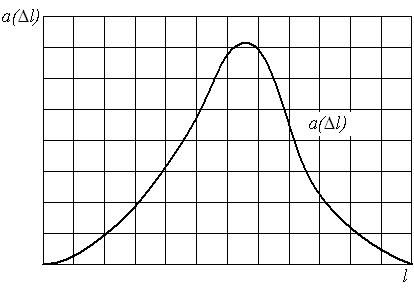 Рис. 1.3. График изменения частоты отказов в зависимости от наработки 1.4 Интенсивность отказов Интенсивность отказов представляет собой условную плотность возникновения отказа объекта, определяемую для рассматриваемого момента времени или наработки при условии, что до этого момента отказ не возник. Иначе интенсивность отказов – это отношение числа отказавших элементов в единицу времени или пробега к числу исправно работающих элементов в данный отрезок времени. Интенсивность отказов обозначается как  и определяется по формуле (1.4): где  Как правило, интенсивность отказов является неубывающей функцией времени. Интенсивность отказов обычно применяется для оценки склонности к отказам в различные моменты работы объектов.На рис. 1.4. представлен теоретический характер изменения интенсивности отказов в функции пробега. 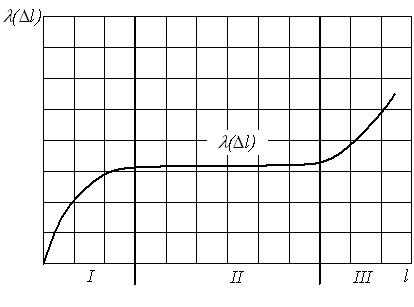 Рис. 1.4. График изменения интенсивности отказов в зависимости от наработки На графике изменения интенсивности отказов, изображенном на рис. 1.4. можно выделить три основных этапа отражающих процесс эксплуатации элемента или объекта в целом. Первый этап, который также называется этапом приработки, характеризуется увеличением интенсивности отказов в начальный период эксплуатации. Причиной роста интенсивности отказов на данном этапе являются скрытые дефекты производственного характера. Второй этап, или период нормальной работы, характеризуется стремлением интенсивности отказов к постоянному значению. В течение этого периода могут возникать случайные отказы, в связи с появлением внезапной концентрации нагрузки, превышающей предел прочности элемента. Третий этап, так называемый период форсированного старения. Характеризуется возникновением износовых отказов. Дальнейшая эксплуатация элемента без его замены становится экономически не рациональной. 1.5 Средняя наработка до отказа Средняя наработка до отказа – это средний пробег безотказной работы элемента до отказа. Средняя наработка до отказа обозначается как L1 и определяется по формуле (1.5):  где li – наработка до отказа элемента; ri – число отказов. Средняя наработка до отказа может быть использована для предварительного определения сроков ремонта или замены элемента. 1.6 Среднее значение параметра потока отказов Среднее значение параметра потока отказов характеризует среднюю плотность вероятности возникновения отказа объекта, определяемая для рассматриваемого момента времени. Среднее значение параметра потока отказов обозначается как Wср и определяется по формуле (1.6):  1.7 Пример расчета показателей безотказности Исходные данные. В течение пробега от 0 до 600 тыс. км, в локомотивном депо произведен сбор информации по отказам ТЭД. При этом количество исправных ТЭД в начале периода эксплуатации составляло N0 = 180 шт. Суммарное количество отказавших ТЭД за анализируемый период составило ∑r(600000) = 60. Интервал пробега принять равным 100 тыс. км. При этом количество отказавших ТЭД по каждому участку составило: 2, 12, 16, 10, 14, 6. Требуется. Необходимо рассчитать показатели безотказности и построить их зависимости изменения во времени. Сначала необходимо заполнить таблицу исходных данных так, как это показано в табл. 1.1. Таблица 1.1.
Первоначально по уравнению (1.1) определим для каждого участка пробега величину вероятности безотказной работы. Так, для участка от 0 до 100 и от 100 до 200 тыс. км. пробега вероятность безотказной работы составит:   Далее, используя зависимость (1.2) произведем расчет вероятности отказа ТЭД.   Произведем расчет частоты отказов по уравнению (1.3).   Далее по уравнению (1.4) произведем расчет интенсивности отказов ТЭД в зависимости от наработки. Первоначально рассчитаем среднее количество работоспособных ТЭД на участке от 0 до 100 тыс. км. пробега:  Тогда интенсивность отказов на участке 0-100 тыс.км. будет равна:  Аналогичным образом определим величину интенсивности отказов для интервала 100-200 тыс. км.   По уравнениям (1.5 и 1.6) определим среднюю наработку до отказа и среднее значение параметра потока отказов.   Систематизируем полученные результаты расчета и представим их в виде таблицы (табл. 1.2.). Таблица 1.2.
Приведем характер изменения вероятности безотказной работы ТЭД в зависимости от пробега (рис. 1.5.). Необходимо отметить, что первой точкой на графике, т.е. при пробеге равном 0, величина вероятности безотказной работы примет максимальное значение – 1.  Рис. 1.5. График изменения вероятности безотказной работы в зависимости от наработки Приведем характер изменения вероятности отказа ТЭД в зависимости от пробега (рис. 1.6.). Необходимо отметить, что первой точкой на графике, т.е. при пробеге равном 0, величина вероятности отказа примет минимальное значение – 0. 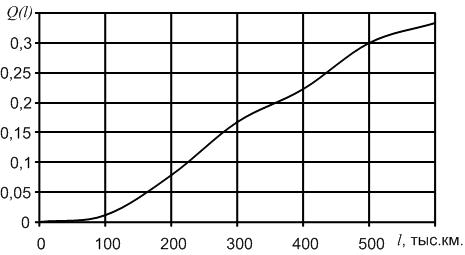 Рис. 1.6. График изменения вероятности отказа в зависимости от наработки Приведем характер изменения частоты отказов ТЭД в зависимости от пробега (рис. 1.7.).  Рис. 1.7. График изменения частоты отказов в зависимости от наработки На рис. 1.8. представлена зависимость изменения интенсивности отказов от наработки. 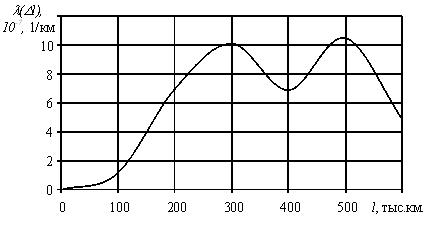 Рис. 1.8. График изменения интенсивности отказов в зависимости от наработки | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
10-7, 1/км