лабораторная по кулинарии2. 1. 16. Маховик, масса которого 6 кг равномерно распределена по ободу радиусом 18 см, вращается на валу с частотой 500 мин Под действием тормозящего момента 10 Нм маховик останавливается.

• Название: 1. 16. Маховик, масса которого 6 кг равномерно распределена по ободу радиусом 18 см, вращается на валу с частотой 500 мин Под действием тормозящего момента 10 Нм маховик останавливается.
• Анкор: лабораторная по кулинарии2
• Дата: 05.12.2021
• Размер: 169.9 Kb.
• Имя файла: Fizika_p_1026.docx
• Тип: Документы; #291725

1.16. Маховик, масса которого 6 кг равномерно распределена по ободу радиусом 18 см, вращается на валу с частотой 500 мин^-1. Под действием тормозящего момента 10 Н·м маховик останавливается. Найти, через какое время он остановится, какое число оборотов он совершит за это время и какова работа торможения.

Дано:
кг
см	м
мин
Н∙м

Решение.

Момент инерции маховика относительно оси вращения как тонкостенного однородного диска равен:

,

где – масса маховика;

– радиус маховика.

Если тормозящий момент , действующий на маховик, постоянный, то постоянным будет и угловое ускорение , с которым маховик будет тормозить.

Запишем для маховика основное уравнение вращательного движения твёрдого тела относительно неподвижной оси:

.

Отсюда найдём величину углового ускорения маховика:

.

Если маховик в начальный момент действия тормозящего момента имел частоту вращения , то его начальная угловая скорость была равна:

.

Закон изменения угловой скорости маховика при равнозамедленном движении:

;

.

Найдём время торможения маховика до полной остановки ( ):

;

;

;

с.

При равнозамедленном движении зависимость угла поворота маховика от времени задаётся уравнением (начальный угол поворота примем ):

;

;

.

Определим угол поворота за время торможения:



Поскольку одному обороту маховика соответствует угол поворота в , то за время торможения маховик сделает число оборотов:

;

.

Поскольку тормозящий момент, действующий на колесо, постоянный, то работа сил торможения при повороте колеса на угол будет равна (учтём, что работа сил торможения отрицательна):

;

Дж.

Ответ: с, , Дж.

1.36. Какова теоретически возможная максимальная работа паровой машины, если в топке котла, питающего паром машину, будет сожжено 100 кг каменного угла с теплотворной способностью 30 МДж? Температура пара 190 °C, температура холодильника 10 °C. Коэффициент полезного действия топки котла 80 %.

Дано:
кг
МДж/кг	Дж/кг
	К
	К

Решение.

При сжигании массы каменного угля выделяется количество теплоты:

,

где – теплотворная способность каменного угля.

Зная КПД топки котла, можем определить, какое количество теплоты пойдёт на нагрев пара:

.

Пусть – теоретически возможная максимальная работа паровой машины. КПД такой паровой машины равен:

.

Максимально возможный КПД будет у паровой машины, работающей по циклу Карно. При этом КПД будет определяться максимальной и минимальной температурами цикла:

.

Приравняем два выражения для КПД цикла и найдём теоретически возможную максимальную работу паровой машины:

;

.

Проверим размерность:

. (верно)

Проведём расчёт:

Дж = 933 МДж.

Ответ: МДж.

2.2. Два одинаковых шарика, обладающих массой 0,6∙10^-3 г каждый, подвешены на шёлковых нитях длиной 0,4 м так, что их поверхности соприкасаются. Угол, на который разошлись нити при сообщении шарикам одинаковых зарядов, равен 60°. Найти заряд.

Дано:
г	кг
м

Решение.
В силу симметрии системы будем рассматривать шарик 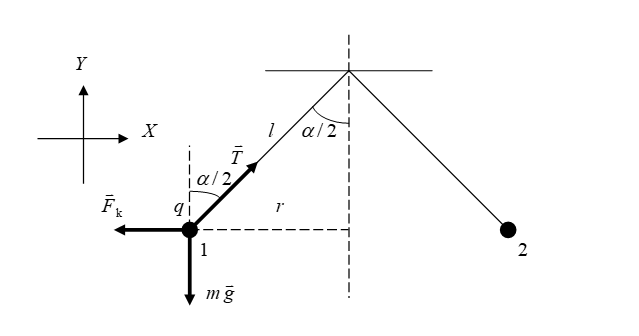(для шарика рассуждения аналогичны).



На шарик будут действовать три силы: сила кулоновского отталкивания со стороны шарика , сила тяжести и сила натяжения нити .

Сила Кулона равна:

,

где Ф/м – электрическая постоянная;

– заряд каждого шарика;

– расстояние между шариками;

– длина нити.

Составим для шарика уравнение по II-му закону Ньютона в векторной форме и в проекциях на оси и :



Из первого уравнения системы получаем:

.

Из второго уравнения системы получаем:

.

Поделим первое уравнение на второе:

;

;

.

Отсюда найдём заряд шарика:

;

.

Проверим размерность:



.

(верно)

Проведём расчёт:

Кл = 7,77 нКл.

Ответ: нКл.

2.31. Найти энергию поляризованного слюдяного диэлектрика, находящегося в конденсаторе, если площадь пластины конденсатора 25 см², толщина диэлектрика – 9 мм и пластины заряжены до напряжения 2 кВ.

Дано:
см2	м2
мм	м
кВ	В

Решение.
Ёмкость плоского конденсатора равна:

,

где Ф/м – электрическая постоянная;

– диэлектрическая проницаемость диэлектрика;

– площадь каждой пластины конденсатора;

– расстояние между пластинами конденсатора.

Найдём энергию электростатического поля плоского конденсатора:

,

где – разность потенциалов между обкладками конденсатора.

Проверим размерность:

. (верно)


Проведём расчёт:
Дж = 29,5 мкДж.

Ответ: мкДж.

3.5. Плоская круглая рамка состоит из 20 витков радиусом 2 см, и по ней течёт ток силой 1 А. Нормаль к рамке составляет угол 90° с направлением магнитного поля напряжённостью 30 А/м. Найти изменение вращающего момента, действующего на рамку, если из 20 витков рамки сделать один круглый виток.

Дано:
см	м
А
А/м

Решение.

На виток с током действует механический вращающий момент:

, (1)

где – магнитный момент витка;

– индукция магнитного поля;

– угол между нормалью к контуру и направлением магнитного поля.

Магнитный момент плоского витка с током равен:

,

где – сила тока в витке;

– площадь витка.

Для круглого витка радиуса получим:

, (2)

где – площадь круглого витка радиусом .

Связь между индукцией и напряжённостью одного и того же магнитного поля в немагнитной среде:

, (3)

где Гн/м – магнитная постоянная.

Подставляя (2) и (3) в (1) и учитывая, что угол , получим:

;

. (4)

В первом случае рамка состоит из витков, на каждый из которых действует механический вращающий момент, определяемый выражением (4), следовательно, на всю рамку будет действовать вращающий момент:

;

. (5)

Периметр одного витка радиуса равен , следовательно, длина проволоки, состоящей из одинаковых круговых витков будет равна:

. (6)

Пусть из этой проволоки сделали один большой круглый виток некоторого радиуса . Тогда можем записать:

. (7)

Приравняем выражения (6) и (7) и найдём радиус большого витка:

;

. (8)

Подставляя (8) в (4), и учитывая, что сила тока в проводе не меняется, найдём вращающий момент, который будет действовать на большой виток:

;

. (9)

С учётом (5) получим:

. (10)

Из (1) следует, что вращающий момент увеличился.

Определим, на сколько увеличился вращающий момент, используя выражения (5) и (9):

;

.

Проверим размерность:

. (верно)

Проведём расчёт:

Н·м = 18,0 мкН·м.

Ответ: мкН·м.

3.31. Какова скорость движения автомобиля, если в его вертикальной антенне длиной 1,5 м индуцируется ЭДС 6·10^-4 В? Горизонтальную составляющую магнитного поля Земли считать равной 14 А/м. Автомобиль движется перпендикулярно магнитному меридиану.

Дано:
м
В
А/м

Решение.

Антенна является проводником. Она движется со скоростью движения автомобиля перпендикулярно магнитному меридиану. За небольшое время антенна пройдёт путь:

.

При этом антенной будет пересечена площадь:

,

где – длина антенны.

Так как поле однородное, то магнитный поток через площадь, пересечённую антенной, будет равен:

,

где – формула, связывающая индукцию и напряжённость одного и того же магнитного поля в немагнитной среде;

Гн/м – магнитная постоянная.

Согласно закону электромагнитной индукции, при этом в антенне возникает ЭДС индукции, равная по величине:

.

Отсюда найдём скорость автомобиля:

.

Проверим размерность:

. (верно)

Проведём расчёт:

м/с.

Ответ: м/с.

4.1. Найти длину волны света, освещающего установку в опыте Юнга, если при помещении на пути одного из интерферирующих лучей стеклянной пластинки (n = 1,52) толщиной 2 мкм картина интерференции на экране смещается на три светлые полосы.

Дано:
мкм

Решение.
Оптическая разность хода лучей в результате внесения пластинки равна:

,

где – толщина пластинки;

– показатель преломления материала пластинки.

С другой стороны, если произошло смещение на полос, то оптическая разность хода лучей равна:

.

Приравнивая два выражения для оптической разности хода, получаем:

.

Отсюда найдём длину волны света:

;

мкм = 347 нм.

Ответ: нм.

4.31. Вычислить период вращения электрона на первой боровской орбите в двукратно ионизированном атоме лития.

Дано:
кг
Кл

Решение.

Двукратно ионизированный атом лития является водородоподобным атомом с зарядом ядра:

,

где – порядковый номер элемента в периодической таблице;

– элементарный заряд.

По теории Бора, электрон в водородоподобном атоме, находящемся в -ом квантовом состоянии, движется по круговой орбите радиуса под действием силы кулоновского притяжения со стороны ядра:

,

где Ф/м – электрическая постоянная.

Сила Кулона центростремительная, то есть электрон имеет нормальное ускорение:

,

где – скорость электрона на -ой орбите.


По второму закону Ньютона можем записать:

,

где – масса электрона.

Отсюда скорость электрона на -ой орбите:

.

По первому постулату Бора, момент импульса электрона в атоме может принимать дискретные значения:

,

где Дж∙с – постоянная Планка.

Тогда скорость электрона на -ой орбите:

.

Найдём радиус -ой орбиты:

;

.

Найдём период обращения электрона на -ой орбите:

.

Для первой орбиты:

с.

Ответ: с.