1. 17. Колебания. Математический и физический маятники
 Скачать 18.27 Kb. Скачать 18.27 Kb.
|
|
1.17. Колебания. Математический и физический маятники. Колебание –процесс, повторяющийся во времени. Время повторения процесса колебаний называется периодом колебаний Т. Число колебаний в секунду f=(1/Т) называется частотой колебаний, единица измерения Герц (Гц). Систему, в которой происходят колебания, называют осциллятором. Если при колебании периодически меняется положение материальной точки или твёрдого тела, то такую систему называют маятником. Простейшим маятником является материальная точка массой m, качающаяся на невесомом подвесе длиной L. Такой маятник называют «математическим». Период его колебаний зависит только от длины подвеса и ускорения силы тяжести g: Т2=(L/g).C его помощью можно находить g. Максимальное отклонение качающейся материальной точки от положения равновесия называется амплитудой колебаний. Если амплитуда колебаний не зависит от времени, то колебания называются незатухающими. Если амплитуда в процессе колебаний уменьшается, колебания называются затухающими. Колебания называются гармоническими, если колеблющаяся величина меняется по закону синуса или косинуса, в противном случае колебания называются ангармоническими. Физический маятник — это твёрдое тело, способное совершать вращательные колебания вокруг оси, смещённой относительно центра инерции на расстояние h. Колеблющейся величиной является угол Ф между вертикалью и прямой, соединяющей ось вращения с центром инерции. При малых углах Ф второй закон Ньютона для вращательного движения твёрдого тела в этом случае имеет вид: J*Ф''=-mghФ, где m-масса тела, J-момент инерции относительно смещённой оси, откуда, обозначив (mgh/J)=ω2, получаем дифференциальное уравнение: Ф''+ω2Ф=0. Решением этого дифференциального уравнения является уравнение свободных незатухающих колебаний физического маятника: Ф=ФмаксСos(ωt+ϕo) или Ф=ФмаксSin(ωt+ϕo), где Фмакс - амплитуда, ϕо - начальная фаза колебаний. Частота свободных незатухающих колебаний физического маятника ω=(mgh/J). Если колеблющееся тело является материальной точкой, подставив значение момента инерции J=mh2, получаем уравнение колебаний математического маятника Ф=ФмаксСоs(ωt+ϕ0) с угловой частотой ω=(g/h). 2.11. Магнитный поток, теорема Гаусса. Работа при перемещении проводника с током в магнитном поле. Электромагнитная индукция. Правило Ленца. Магнитный поток Ф (поток магнитной индукции) через поверхность площадью S - величина, равная произведению модуля вектора магнитной индукции на площадь S и косинус угла а между вектором Ф=BScos В СИ единица магнитного потока 1 Вебер (Вб) - магнитный поток через поверхность площадью 1 м 2 , расположенную перпендикулярно направлению однородного магнитного поля, индукция которого равна 1 Тл: 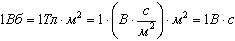 Теорема Гаусса: Поток вектора магнитной индукции (магнитный поток) сквозь произвольную замкнутую поверхность равен нулю: Работа по перемещению проводника с током в магнитном полеравна произведению силы тока на магнитный поток, пересеченный движущимся проводником: dA = I * dФm, где dФm - поток вектора магнитной индукции, пронизывающий площадь, пересекаемую проводником в магнитном поле. Электромагнитная индукция-явление возникновения электрического тока в замкнутом проводящем контуре при любом изменении магнитного потока, пронизывающего контур. Возникающий в замкнутом контуре, индукционный ток имеет такое направление, что своим магнитным полем противодействует тому изменению магнитного потока, которым он вызван (правило Ленца). |
