практические. Практическое задание по электроники. 1. 2 (c 30 по 38 канал) 23(с 20 по 60 канал)

• Название: 1. 2 (c 30 по 38 канал) 23(с 20 по 60 канал)
• Анкор: практические
• Дата: 04.04.2023
• Размер: 1.21 Mb.
• Имя файла: Практическое задание по электроники.docx
• Тип: Документы; #1036420
• страница: 5 из 11

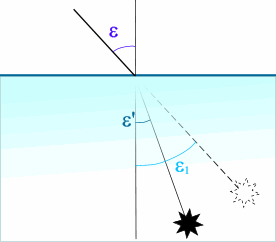
1.2. Расчет световых величин

Задача 1.

Потоком освещается круглая площадка. Освещенность равна 2 лк. Радиус площадки равен 1 м. Определить поток.

Решение:

Освещенность - величина, обратно пропорциональная площади. Сначала необходимо определить площадь объекта:

S=π·r²=3.14·1·1=3.14 (м²)

Поток находится исходя из соотношений для освещенности:

E=Ф/S, значит Ф=Е·S=2·3.14=6.28 (лм)

Ответ: Поток Ф=6.28 лм.

Задача 2.

Светимость круглой площадки 12.7 лм/м². Поток, излучаемый площадкой составляет 10 лм. Определить радиус площадки.

Решение:

Светимость М=Ф/S

Следовательно, площадь равна: S=Ф/М=0.785 (м²)

S=π·r²=3.14·r², откуда r²=S/π=0.25 (м²)

Следовательно, радиус r=0.5 (м)

Ответ: Радиус площадки составляет 0.5 м.

1.3. Определение параметров излучателей различных типов

Задача 1.

Полный поток от сферического ламбертовского излучателя в телесном угле, образованном вращением плоского угла σ=90° составляет 40 лм. Определить силу света излучателя.

Решение:

Сила света рассчитывается исходя из соотношения: I=Ф/Ω

Сначала производится расчет телесного угла: Ω=4·π·sin²(σ/2)=4·π·2/4=2π (ср)

Тогда сила света: I=Ф/Ω=40/6.28=6.36 (лм/ср)

Ответ: I=6.36 лм/ср

Задача 2.

Сила света плоского ламбертовского излучателя составляет 31.83 кд. Телесный угол Ω образован вращением плоского угла σ=90°. Определить полный поток от излучателя.

Решение:

Полный поток от плоского ламбертовского излучателя:

Ф=(π·I·sin²σ)/2

Ф=31.8·3.14·1/2=100/2=50 (лм)

Ответ: Полный поток Ф=50 лм

1.4. Определение параметров рассеивающих поверхностей

Задача 1.

Поток 40 лм освещает квадратный рассеиватель. Сторона квадрата 2 м. Степень белизны поверхности 0.5. Определить яркость рассеивателя.

Решение:

Задача решается в несколько этапов:

Яркость рассеивателя: рассчитывается через освещенность.

Сначала определяем освещенность площадки, Е=Ф/S=40/4=10 (лк)

Затем яркость L=0.5·10/π=5/3.14=1.59 (кд/м²)

Ответ: Яркость L=1.59 кд/м².

Задача 2.

На рассеивателе создана освещенность 10 лк. Яркость рассеивателя 1.59 кд/м². Определить коэффициент Альбедо поверхности.

Решение:

По той же формуле имеем: α=L·π/E=1.59·3.14/10=0.5

Ответ: Коэффициент Альбедо α=0.5

2.2. Задачи на закон преломления

Задача

Объект находящийся в воде, виден под углом 60°. Определить угол наклона преломленного луча в воде, если показатель преломления n=1.33.

Решение:

Угол, под которым виден объект - это угол мнимый, а реально это угол, под которым мы смотрим на объект. Таким образом, нам даны ε₁ и n.

По закону преломления n·sin ε=n'·sin ε'

sin(ε')=sin(ε)/n'

sin(ε')=sin(60°)/1.33=0.709

Преломленный угол ε' равен 40°30'

Ответ: Угол ε'=40°30'

2.3. Задачи на закон отражения

Задача 1.

Определить угол поворота плоского зеркала γ относительно оси ОХ, если направление падающего луча задано углом α=10°, а направление отраженного луча β=80°.

Решение:

Угол падения равен углу отражения. Если угол отражения не равен углу падения, значит, зеркало повернуто. Разница между углами составляет 70°. Как известно, угол поворота луча в два раза больше угла поворота зеркала.

В нашем случае угол поворота луча составляет 70 °. Это означает, что γ=35°.

Ответ: γ=35°

2.3.3. Два плоских зеркала, расположенных под углом

Угловое зеркало - часто используемая в оптике конструкция.



Зависимость между направлениями падающего и выходящего лучей для системы, состоящей из двух зеркал : .

1. Угол отклонения равен удвоенной величине угла между зеркалами.
2. При повороте двойного зеркала угол отклонения не изменяется
3. Угол отклонения не зависит от угла падения

Задача 2.

Угловое зеркало изменяет направление падающего на него луча на величину γ=30°. Определить угол при вершине зеркала.

Решение:

Угловое зеркало поворачивает луч на угол, равный удвоенному углу при вершине зеркала.

Значит, угол при вершине равен 15°.

Ответ: Угол при вершине двойного зеркала равен 15°.