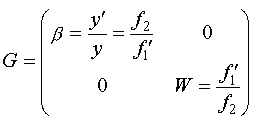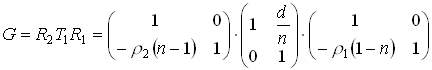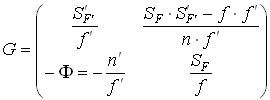практические. Практическое задание по электроники. 1. 2 (c 30 по 38 канал) 23(с 20 по 60 канал)
 Скачать 1.21 Mb. Скачать 1.21 Mb.
|
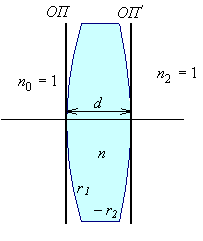
5.1. Расчет матрицы Гаусса оптической системыЗначения элементов матрицы Гаусса для сопряженных плоскостей:А носит значение линейного увеличения. Для случая сопряженных опорных плоскостей элемент B=0. Элемент С не зависит от положения опорных плоскостей и всегда равен оптической силе c обратным знаком. Элемент D - величина обратная элементу А, и для афокальной системы имеет смысл углового увеличения: D= Задача 1.Предмет величиной 5 мм находится на расстоянии 150 мм перед выпуклоплоской линзой с радиусом поверхности 50 мм, толщиной 10 мм и показателем преломления 1.5. Определить размер и положение изображения относительно последней поверхности S'. Решить задачу с помощью матриц. Осуществить проверку решения. Решение:Сначала необходимо определить параксиальные характеристики системы. По соотношениям, приведенным в практической работе 4, получим: f'=100; SH=0 ; S'H=-6.67. 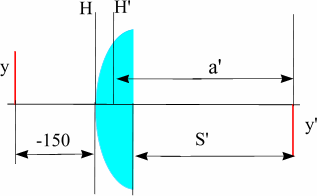 Составляем матрицу преобразования лучей системой, опорные плоскости которой расположены в плоскостях предмета и изображения для данной задачи. Очевидно, что преобразований будет три, от предмета до главной плоскости - перенос T0, на главных плоскостях - преломление R1, до изображения - перенос T1. Итак, матрицы: 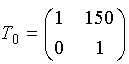 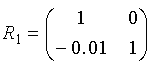 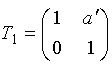 Матрица всей системы G=T1·R1·T0. Правила перемножения матриц можно посмотреть в "Приложении П3. Арифметические операции над матрицами". Результат произведения матриц даст нам матрицу с одним неизвестным - a': 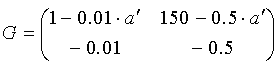 Условие сопряжения опорных плоскостей гласит, что элемент матрицы В=0. Составляем уравнение 150-0.5a'=0, значит, a'=300. S'=S'H+a'=300-6.67=293.33 мм. Определение величины изображения. Изображение y'=y·β Увеличение системы равно значению элемента А. β=1-3= -2. y'= -2·5= -10. Ответ: S'=293.33 мм, y'= -10 мм. Проверка:100/a'=1-(-100)/(-150)=1-2/3=1/3 a'=300, значит, S'=293.33 мм Увеличение 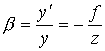 , значит, β= -(-100)/(-50)= -2. , значит, β= -(-100)/(-50)= -2.Ответ: S'=293.33 мм, y'= -10 мм. Задача 2.Фокусное расстояние линзы f'=100 мм. Предмет находится на расстоянии a= -150 мм от передней главной плоскости линзы. Изображение формируется на расстоянии 300 мм от задней главной плоскости линзы. Найти значения элементов матрицы преобразования лучей при условии, что опорные плоскости совпадают с плоскостями предмета и изображения. Решение:Все элементы матрицы имеют свое назначение. Элементы A и D зависят от линейного увеличения системы. β= -f/z= -(-100)/(a-f)=100/(-150+100)=-2. Тогда A=-2; D=1/А=-0.5. Необходимо определить силу линзы Ф=1/f'=0.01, значит C=-0.01. Элемент В для сопряженных плоскостей равен 0. Ответ: Матрица преобразования лучей данной системой: 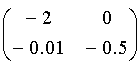 . .5.2. Расчет характеристик многокомпонентных оптических систем с использованием матрицВопросы расчета характеристик можно рассмотреть в основных определениях и соотношениях в параграфе "6.3. Матрицы оптической системы, состоящей из нескольких компонентов" 5.2.1. Пакет из плоскопараллельных слоевПакет плоскопараллельных слоев - это система, состоящая из сред с различными показателями преломления. Оптическая сила таких элементов равна нулю 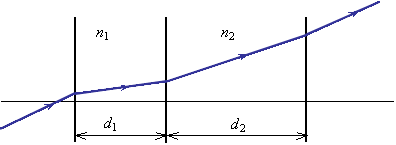 Приведенная матрица переноса для пакета плоскопараллельных слоев будет выглядеть следующим образом: 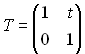 , где , где 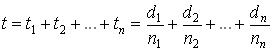 Задача 1.
Необходимо определить приведенные толщины слоев t: t1=10.5/2.1=5; t2=9/1.5=6; t3=2. И общая толщина всего пакта слоев равна сумме приведенных толщин и воздушных промежутков: t=5+11+6+5+2=29 мм. Ответ: Матрица преобразования пакета: 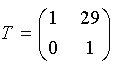 Причем, вопрос в задачах может касаться не только всей матрицы, но и отдельных ее элементов. Как видите, сложный расчет в данной матрице касается только одного элемента B, тогда как остальные требуют не расчета, а простого знания структуры матрицы. 5.2.2. Оптическая система с нулевыми расстояниями между компонентамиРассмотрим оптическую систему, в которой расстояния между компонентами равны нулю 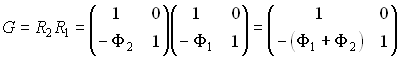 то есть оптические силы таких компонент складываются: Задача 2.Компонент из трех тонких линз (с нулевыми расстояниями между ними) находится в воздухе. Определить значение элемента C матрицы преобразования лучей. Известно, что фокусные расстояния имеют следующие значения: f'1=10, f'2=-20 и f'3=5 мм. РешениеОбщая оптическая сила этой системы будет равна сумме отдельных оптических сил. Необходимо определить приведенные силы линз Ф: Ф1=0.1, Ф2=-0.05 и Ф3=0.2. Общая суммарная сила системы Ф=0.3-0.05=0.25 [1/мм=кдптр]. Элемент матрицы С=-Ф=-0.25 Ответ: Элемент матрицы С=-0.25 В задачах может быть предложен поиск и других элементов матрицы, но расчета требует только элемент С, а остальные нам известны заранее. Также задачи могут касаться поиска фокусного расстояния одного из элементов по заданной общей оптической силе. 5.3. Расчет характеристик двухкомпонентных оптических систем с использованием матриц5.3.1. Двухкомпонентная оптическая системаРассмотрим оптическую систему, состоящую из двух компонентов, разделенных ненулевым промежутком. Матрица такой системы: Задача 1.Оптические силы первого и второго компонентов двухкомпонентной оптической системы равны 10 и 1 дптр соответственно, расстояние между компонентами равно 50 мм. Чему равна оптическая сила системы? Решение:Общая оптическая сила этой системы будет равна : Ф=1+10-1·10·0.05=11-0.5= 10.5 (дптр). Ответ: Оптическая сила Ф=10.5 дптр. 5.3.2. Афокальные (телескопические) системыВ афокальных (телескопических) системах линейное и угловое увеличение не зависят от положения сопряженных опорных плоскостей и, следовательно, не зависят от положения предмета и изображения. Линейное увеличение такой системы: 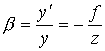 Подробнее этот вопрос рассмотрен в параграфе "6.3.3. Двухкомпонентная оптическая система". Задача 2.Дана афокальная система из двух линз: f'1=20 мм, f'2=-40 мм. Найти угловое увеличение системы. Решение:
Ответ: Линейное увеличение β=2; угловое W=0.5. 5.4. Расчет параксиальных характеристик линзы с использованием матрицМатрица тонкой линзыЛинзы и диоптрические (преломляющие) элементы можно рассматривать как многокомпонентные системы, состоящие из поверхностей, разделенных промежутками. Например, линзу в воздухе можно представить в матричном виде:
ЗадачаПеред стеклянным стержнем с выпуклой поверхностью радиусом 20 мм на расстоянии 100 мм расположен предмет. Величина предмета y=10 мм. Определить величину и положение изображения внутри стеклянного стержня, если показатель преломления среды стержня n=1.5. Решение:Сначала необходимо определить этапы построения изображения этой системой. Этапа получается три: перенос от предмета до преломляющей поверхности - T0, преломление - R, перенос до изображения - T1. Определим матрицы: 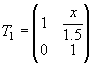 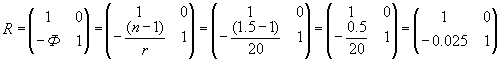 Произведение матриц даст нам матрицу G преобразования лучей этой системой. 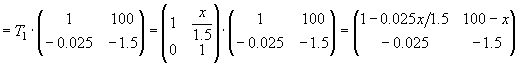 Положение изображения: Для сопряжения ОП и ОП' условие B=0. 100-x=0. Значит, х=100 - изображение находится на расстоянии 100 мм от края стержня. Размер изображения: Величина A - линейное увеличение, а величина D - обратная ей. Значит, β=1/-1.5=-0.66. Величина изображения y'= β·y=-0.66·10=-6.6 мм. Изображение будет перевернутым. Ответ: Перевернутое изображение величиной 6.6 мм будет находиться внутри стержня на расстоянии 100 мм от края. Пример определения параксиальных характеристик системы по матрице Гаусса изложен в "Приложении П2. Вычисление и отображение параксиальных характеристик при помощи матричной оптики". |