www.maxXP.narod.ru - gold collection from MaxXP
Оглавление.
Геометрическая оптика
Интерференция световых волн
Дифракция света
Фотометрия и термодинамика излучения
Поляризация света
Дисперсия света
Перенос излучения в мутных средах
Квантовые свойства света
Фотохимическое действие света
Элементы атомной физики
Элементы ядерной физики
Бонус. Формулы для задач
1. Геометрическая оптика. Границы применимости геометрической оптики Понятие оптического луча. Законы геометрической оптики. Центрированная оптическая система. Кардинальные элементы центрированной оптической системы: фокусы, фокальные плоскости, главные плоскости и главные точки, узлы. Формула оптической системы Диафрагмы. Действующая диафрагма. Вводной и выходной зрачок оптической системы Светосила оптической системы. Тонкая линза. Построение изображений в оптических системах. Лупа, зрительная труба, микроскоп. Глаз и зрение.
Основные понятия геометрической оптики.
Геометрическая оптика - раздел оптики, в котором законы распространения света в прозрачных средах рассматриваются с точки зрения геометрии. Волновая оптика при λ = 0 переходит в геометрическую. Геометрическая оптика оперирует понятием световых лучей, независимых друг от друга и подчиняющихся известным законам преломления и отражения.
Световой луч - это линия, вдоль которой распространяется энергия излучения. Световому лучу в волновой оптике соответствует нормаль (перпендикуляр) к волновой поверхности.
Оптической системой называется совокупность оптических деталей (призмы, линзы, зеркала), предназначенных для преобразования пучков световых лучей посредством преломления и отражения на поверхностях, которыми ограничены оптические детали.
Оптическую систему называют центрированной, если центры сферических поверхностей или оси симметрии других поверхностей, образующих оптическую систему, расположены на одной прямой, называемой оптической осью.
Если пучок световых лучей, идущий из какой-либо точки Р (см.рис1), после прохождения через оптическую систему пересекается в точке Р', то точка Р' называется изображением точки Р. Изображение, образованное пересечением лучей выходящих из оптической системы, называют действительным, а изображение, образованное пересечением геометрических продолжений этих лучей - мнимым.
Р
ис.1. Изображение точки в оптической системе: а - действительное, б - мнимое.
Для того, чтобы подчеркнуть, что лучи строго пересекаются только в одной точке Р' изображение в этом случае называют стигматическим.
Пучок же лучей, исходящих из одной точки или сходящихся в одной точке, называется гомоцентрическим (рис.2). Точка пересечения параллельного пучка световых лучей находится в бесконечности.

Рис.2. Гомоцентрические пучки лучей: а - расходящийся, б -сходящийся, в - параллельный.
В геометрической оптике изображение точки принято обозначать той же буквой, что и предмет, но со штрихом. Это относится и к другим обозначениям (лучам, плоскостям, углам, отрезкам, показателям преломления и т.д.).
Любой предмет или изображение рассматриваются как совокупность предметных точек или изображений этих точек. Две точки, одна из которых является изображением другой, называют сопряженными. Все пространство, в котором распространяются пучки лучей, можно разделить на две части. Пространство, в котором находятся точки предметов, называется пространством предметов. Пространство, в котором расположены изображения точек пространства предметов, называют пространством изображений.
В
геометрической оптике используют правило знаков (рис.3).
Рис.3. Пример применения правила знаков.
Положительное направление распространения света слева направо. Для каждого отрезка указывается направление отсчета.
Отрезки вдоль оптической оси считаются положительными, если их направление отсчета совпадает с направлением распространения света.
Отрезки, перпендикулярные к оптической оси, считают положительными, если они расположены над оптической осью и отрицательными, если они расположены под осью.
Угол считается положительным, если образуется вращением оси, от которой ведется отсчет по часовой стрелке, и отрицательным в противном случае.
Отрезки, характеризующие положение предметов и изображений, отсчитываются от кардинальных элементов оптической системы.
Кардинальные элементы оптической системы
Идеальная оптическая система обладает рядом кардинальных элементов - передний и задний фокусы, передние и задние главные и узловые точки, передние и задние фокальные и главные плоскости, переднее и заднее фокусные расстояния.
Знание четырех кардинальных точек (обычно это фокусы и главные точки) полностью определяет работу оптической системы, т.е. мы можем построить изображение любой точки, пользуясь только кардинальными элементами и совершенно не рассматривая действительного хода лучей в данной оптической системе.
Задний фокус и задняя фокальная плоскость оптической системы.
Задним фокусом оптической системы называют изображение бесконечно удаленной точки, расположенной на оптической оси.
Л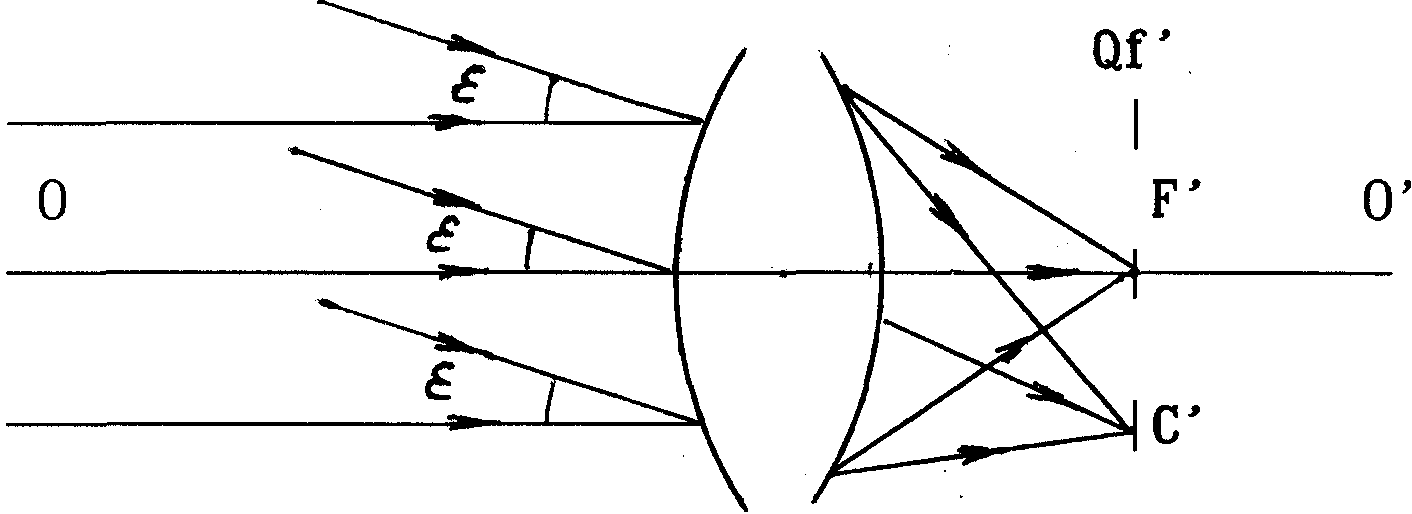
учи, выходящие из бесконечно удаленной точки на оптической оси, падают на оптическую систему параллельно оптической оси. Поэтому можно сказать, что задним фокусом оптической системы называется точка (F'), в которой собирается пучок лучей, падающих на систему параллельно ее оптической оси (рис.5).
Рис.5. Задний фокус и задняя фокальная плоскость оптической системы.
Плоскость (Qf), проходящая через задний фокус и перпендикулярная оптической оси, называется задней фокальной плоскостью оптической системы. Эта плоскость является изображением бесконечно удаленной плоскости.
Параллельный пучок лучей, падающий на оптическую систему под углом к оптической оси (), идет из бесконечно удаленной точки, расположенной вне оптической оси, и после выхода из оптической системы собирается в сопряженной точке С', которая находится вне оптической оси, в задней фокальной плоскости.
Передний фокус и передняя фокальная плоскость оптической системы.
Точку F на оптической оси в пространстве предметов, сопряженную с бесконечно удаленной точкой на оси в пространстве изображений, называют передним фокусом оптической системы.
Р
ис.6. Передний фокус и передняя фокальная плоскость оптической системы.
Всякий луч, входящий в оптическую систему через передний фокус, выходит из системы параллельно ее оптической оси. Если параллельный пучок идет в обратном направлении, то лучи соберутся в переднем фокусе системы (рис.6).
Плоскость Qf, перпендикулярная оптической оси и проходящая через передний фокус, называется передней фокальной плоскостью.
Передняя фокальная плоскость сопряжена с бесконечно удаленной плоскостью пространства изображений.
Пучок лучей, выходящий из любой точки C передней фокальной плоскости Qf, выходит из оптической системы наклонным пучком параллельных лучей.

Передняя и задняя главные плоскости и главные точки оптической системы.
Две сопряженные и перпендикулярные оптической оси плоскости, в которых линейное увеличение равно плюс единице ( = +1), называются передней и задней главными плоскостями Qh и Qh Точки их пересечения с оптической осью называются главными точками Н и Н
Любой отрезок в передней главной плоскости изображается равным и одинаково расположенным отрезком в задней главной плоскости. Отсюда следует, что входящий в оптическую систему и выходящий из нее лучи,пересекают главные плоскости на равных высотах h = h.
Таким образом действие всех преломляющих поверхностей оптической системы для лучей, идущих из бесконечности, можно свести к действию плоскости, перпендикулярной оптической оси, содержащей в себе точку пересечения лучей входящих в эту систему и выходящих из нее. Для лучей, идущих слева направо, это будет задняя главная плоскость, а для лучей, идущих справа налево - передняя главная плоскость (см.рис.7).
Положение фокусов и главных плоскостей определяют путем расчета или графического построения хода лучей, параллельных оптической оси, в прямом и обратном направлениях. При построениях изображений в оптический системе можно считать, что между главными плоскостями лучи идут параллельно оптической оси.
Переднее и заднее фокусные расстояния.
Р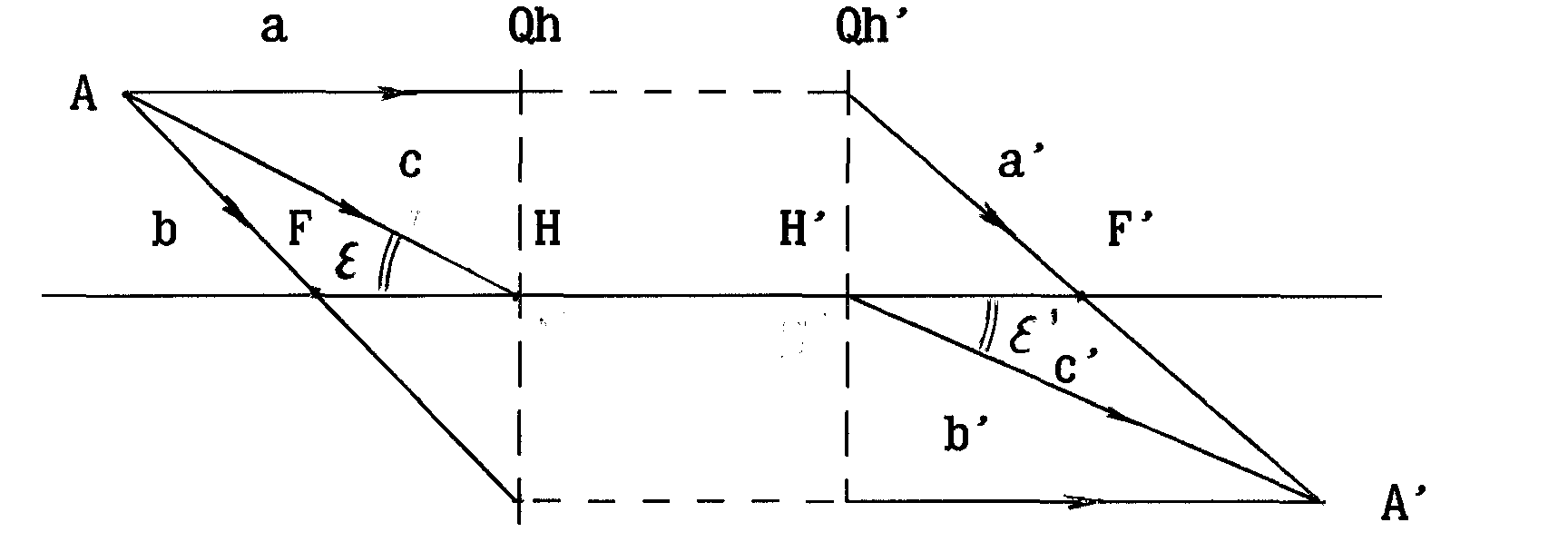
асстояние HF от передней главной точки Н до переднего фокуса F является передним фокусным расстоянием оптической системы – f,
Рис.7. Графическое определение положения главных плоскостей и фокусов оптической системы: а - задних, б - передних.
а расстояние H'F'-от задней главной точки Н' до заднего фокуса F ' - задним фокусным расстоянием f ′ (рис.7).
Фокусные расстояния отсчитывают от соответствующих главных точек с учетом правила знаков. Если оптическая система находится в однородной среде, например в воздухе ( n = n' = 1), то f ′ = -f, т.е. фокусные расстояния равны по абсолютному значению.
В общем случае – f ′ / f = n/n'. Так как n > 0 и n' > 0, то фокусные расстояния всегда имеют разные знаки.
Обычно оптическую систему характеризуют задним фокусным расстоянием, поэтому, если f ′ > 0, то система считается положительной, если
f '< 0, то - отрицательной.
Узловые точки оптической системы.
Точки предмета и изображения, лежащие на оптической оси, для которых угловое увеличение равно плюс единице ( = +1), называются узловыми точками оптической системы N и N
Будем в дальнейшем рассматривать только оптические системы расположенные в однородной среде, для которых n = n , f = f, а следовательно, узловые точки N, N и главные точки H, H такой системы совпадают.
В этом случае сопряженные лучи, проходящие через главные точки H и H параллельны друг другу (рис.8), т.е. = '.
Построение изображений и хода лучей в идеальной оптической системе.
Графическое решение задачи построения изображения предмета в оптической системе сводится к построению изображения отдельных точек предмета, а в конечном итоге к построению хода лучей через оптическую систему. При этом используются свойства кардинальных элементов идеальной оптической системы.Для построения любой точки предмета достаточно построить ход хотя бы двух лучей, проходящих через предметную точку. Точка пересечения этих лучей после прохождения их через оптическую систему будет изображением предметной точки.
Обычно для построения используют так называемые характерные лучи, ход которых в оптической системе хорошо известен, т.е. лучи, проходящие через фокусы и главные (узловые) точки оптической системы
Луч (а), проходящий через предметную точку (А) и падающий на систему параллельно оптической оси, после преломления на задней главной плоскости (Oh)' проходит через задний фокус (F').
Луч (b), проходящий через предметную точку и передний фокус, после преломления на передней главной плоскости идет параллельно оптической оси.
Л
уч (c), проходящий через предметную точку и переднюю главную (узловую) точку, выходит из задней главной (узловой) точки параллельно падающему лучу ( = ) .
Этими тремя лучами удобно пользоваться, если предметная точка расположена вне оптической оси. Если же точка расположена на оптической оси, то все три описанных выше луча совпадают с оптической осью.
Поэтому для построения изображения точки, расположенной на оптической оси, необходимо построить ход хотя бы одного луча, пересекающего оптическую ось в предметной точке, и найти точку пересечения этого луча после выхода из оптической системы с оптической осью. Эта точка и будет изображением исходной предметной точки.
Рис.9. Построение хода лучей в положительной (а) и отрицательной (б) оптической системе. 1 - заданный луч, 2 - вспомогательный луч.
На рис.9 показаны четыре способа построения хода лучей через положительную и отрицательную оптические системы. Для построения используются вспомогательные лучи, проходящие через фокусы или главные точки.
Точки, общие для заданного и вспомогательного лучей в передней фокальной плоскости, обозначены точкой С, а точки общие для тех же лучей в задней фокальной плоскости обозначены соответственно через С'. Лучи, выходящие из точек С, после прохождения оптической системы будут параллельными между собой. Параллельные лучи, падающие на оптическую систему соберутся в точке С'.
Тонкая линза
Простейшей центрированной оптической системой является линза. Она представляет собой прозрачное (обычно стеклянное) тело, ограниченное двумя сферическими поверхностями1 (в частном случае одна из поверхностей может быть плоской). Точки пересечения поверхностей с оптической осью линзы называются вершинами преломляющих поверхностей. Расстояние между вершинами именуется толщиной линзы. Если толщиной линзы можно пренебречь по сравнению с меньшим из радиусов кривизны ограничивающих линзу поверхностей, линза называется тонкой.
Р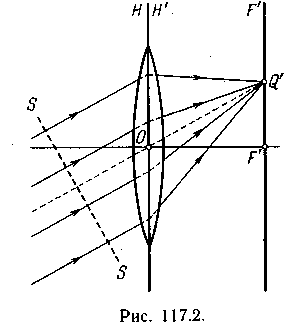 асчеты, которых мы не приводим, дают, что в случае тонкой линзы главные плоскости Я и Я' можно считать совпадающими и проходящими через центр линзы О (рис. 117.1). Для фокусных расстояний тонкой линзы получается выражение асчеты, которых мы не приводим, дают, что в случае тонкой линзы главные плоскости Я и Я' можно считать совпадающими и проходящими через центр линзы О (рис. 117.1). Для фокусных расстояний тонкой линзы получается выражение  (117.1) (117.1)
здесь п — показатель преломления линзы, п0 — показатель преломления среды, окружающей линзу, Ri и Rz— радиусы кривизны поверхностей линзы. С радиусами кривизны нужно обращаться, как с алгебраическими величинами: для выпуклой поверхности (т. е. в случае, когда центр кривизны лежит справа от вершины) радиус кривизны нужно считать положительным, для вогнутой поверхности (т. е. в случае, когда центр кривизны лежит слева от вершины) радиус нужно считать отрицательным. Если показатели преломления сред, находящихся по обе стороны тонкой линзы, одинаковы, то узлы N и N' совпадают с главными точками, т. е. помещаются в центре линзы О. Следовательно,
в этом случае любой луч, идущий через центр линзы, не изменяет своего направления. Если показатели преломления сред перед и за линзой неодинаковы, узлы не совпадают с главными точками, так что луч, идущий через центр линзы, претерпевает излом.
Параллельный пучок лучей после прохождения через линзу собирается в одной из точек фокальной плоскости. Линза не является идеальной оптической системой.
Оптические системы
Д
ля исправления многочисленных дефектов изображения, создаваемых одиночной линзой, в оптических приборах применяют системы различных линз, изготовленных из разных сортов стекла. Обычно используются центрированные оптические системы, в которых центры кривизны всех последовательных сферических поверхностей раздела расположены на одной прямой, являющейся оптической осью системы.
Такие хорошо скорректированные оптические системы близки к идеальным, т. е. можно практически считать, что пучок лучей, исходящих из светящейся точки А, после многочисленных преломлений внутри системы соберется в одной точке А', являющейся изображением точки А. Лучи, падающие параллельно оптической оси (от бесконечно удаленного источника), после прохождения оптической системы соберутся в одной точке Ф2, которая, как и в случае одной линзы, называется задним главным
фокусом системы. На рис. 1.44 показано пунктиром, что продолжения падающих и выходящих лучей в этом случае пересекаются в точках некоторой плоскости Я2, перпендикулярной к оптической оси и носящей название задней главной плоскости системы. Аналогичным образом могут быть построены передний главный фокус Фх и передняя главная плоскость Яа. Все лучи, исходящие из Фг, как бы изламываются на главной плоскости Ht'и выходят параллельно оптической оси. Если среда до и после оптической системы одинакова (например, воздух), то оба главных фокусных расстояния Ф1Н1и Ф2Я2 одинаковы.
'Для тонкой линзы обе главные плоскости сливаются в одну. Для сложной оптической системы эти плоскости различны и могут располагаться как внутри, так и вне системы, несимметрично относительно -поверхностей, ограничивающих систему.
Е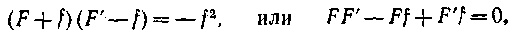 сли известны положения главных фокусов и главных плоскостей системы, то построение изображений производится аналогично тонкой линзе. Как видно из рис. 1.44, вся разница состоит в том, что расстояния Fи F' до предмета и его изображения должны отсчитываться не от центра, как в случае тонкой линзы, а от соответственных главных плоскостей. При этом остаются в силе все формулы для увеличений, например: сли известны положения главных фокусов и главных плоскостей системы, то построение изображений производится аналогично тонкой линзе. Как видно из рис. 1.44, вся разница состоит в том, что расстояния Fи F' до предмета и его изображения должны отсчитываться не от центра, как в случае тонкой линзы, а от соответственных главных плоскостей. При этом остаются в силе все формулы для увеличений, например:
(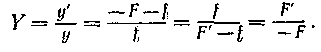 9.1) 9.1)
Отсюда (см выше и правее)
и, разделив на fFF', после преобразований получаем: (9.2)
— соотношение, вполне аналогичное формуле тонкой линзы (8.4).
Оптические приборы широко применяются для расширения возможностей визуального наблюдения. Поскольку при этом изображения получаемые в оптическом приборе, рассматриваются глазом, то требования, предъявляемые к этим изображениям, зависят от свойств человеческого глаза как оптической системы. Не касаясь общеизвестных деталей физиологического строения глаза, отметим здесь лишь две его особенности, существенные с рассматриваемой точки зрения:
1. Основной линзой глаза является хрусталик х, дающий изображение предмета Р на сетчатой оболочке С, как показано на рис. 1.45. Показатель преломления п стекловидной жидкости, заполняющей глаз за хрусталиком, отличен от показателя преломления воздуха («1) перед хрусталиком. Применяя выведенную для такого случая формулу (8.6), имеем:
(9.3)
г де F— переднее фокусное расстояние хрусталика. де F— переднее фокусное расстояние хрусталика.
Для глаза величины F' и п постоянны. Для того чтобы изображение предмета, находящегося на различных расстояниях Fот
глаза,, попадало на сетчатую оболочку, необходимо с изменением Fменять в соответствии с (9.3) фокусное расстояние хрустали-'йа /. Для этого служат специальные мышцы, деформирующие хрусталик и позволяющие аккомодировать глаз в
очень широких пределах от |F| =оо до некоторого |F|MnH. Абсолютная величина расстояния ясного видения Для нормального глаза составляет \Р\ЫВЯ=25 см. У близорукого глаза |f |мин<25 см, а у дальнозоркого | Ркия \ >25 см.
2. Свет, попадая на сетчатую оболочку, вызывает химическую реакцию разложения зрительного пурпура, заключенного в так называемых палочках и колбочках, и таким путем раздражает окончания зрительного нерва. Эти раздражения передаются в головной мозг и создают там зрительные ощущения.
Сетчатая оболочка глаза не сплошная. Окончания зрительного нерва находятся на некотором, хотя и небольшом, расстоянии друг от друга. Если изображение предмета будет столь малым, что покроет лишь один светочувствительный элемент сетчатки, то глаз будет воспринимать этот предмет как одну светящуюся точку. Для того чтобы изображения крайних точек предмета попадали на соседние светочувствительные элементы, этот предмет должен быть виден под некоторым минимальным углом зрения. Глаз не будет различать деталей слишком малых или слишком удаленных предметов и воспримет их как точечные.
Для различения близких, но малых, или больших, но далеких, предметов служат различные визуальные оптические приборы. Как показывает приведенное рассмотрение оптических свойств глаза, основной задачей визуальных приборов является увеличение угла зрения, под которым рассматривается предмет глазом.
Светосила оптической системы.
Число изображений определяется числом монохроматических составляющих в спектре источника, а их интенсивность - спектральной яркостью излучения в каждой длине волны и параметром спектрального прибора - его светосилой.
Схематический ход лучей и принципы действия визуальных приборов.
1. Лупа представляет собой короткофокусную собирательную линзу (или систему линз). Малый предмет А В высотой у помещают, как показано на рис. 1.47, несколько ближе главного
фокуса, так, чтобы его мнимое изображение А 'В' получилось на расстоянии ясного видения 25 см. Угол а', под которым (•дно это изображение, определится из условия
Если бы предмет наблюдался невооруженным глазом, то его пришлось бы поместить на расстояние ясного видения и он был бы виден под углом а, определяемым из условия
Следовательно, угловое увеличение, даваемое лупой, равно: (9.5) (9.5)
Уменьшение фокусного расстояния / связано с увеличением кривизны и уменьшением радиуса кривизны (а следовательно, и диаметра) лупы по формуле (8.5). При пстекла=1>5 и RZ=—R1='K
для двояковыпуклой линзы имеем f=R. Поэтому лупа практически не может увеличивать более чем в 25—40 раз.
2. Микроскоп, как и лупа, служит для рассматривания близких, но очень мелких предметов, требующих значительного увеличения. Как показано на рис. 1.48, микроскоп состоит из двух систем линз — объектива Об и окуляра О/с, расстояние между которыми можно варьировать, изменяя длину тубуса.
Р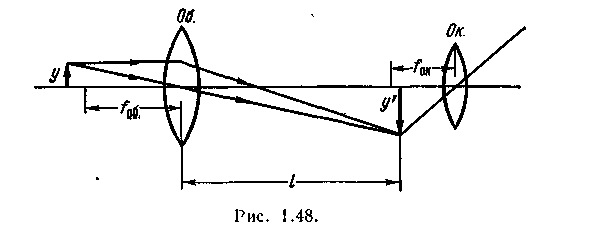 ассматриваемый предмет у помещают на расстояние, несколько превышающее главное фокусное расстояние объектива FОб. ассматриваемый предмет у помещают на расстояние, несколько превышающее главное фокусное расстояние объектива FОб.
Изменяя длину тубуса, получают изображение предмета у', увеличенное в ///Об раз. Это линейно увеличенное изображение рассматривают в окуляр, как в лупу. Таким образом, полное угловое увеличение микроскопа равно: (9.6)
и при достаточно большом отношении ///06 можно получать общее увеличение порядка 1500—2000 раз. Фактически предел увеличения микроскопа ставится волновыми свойствами света (см. § 15).
3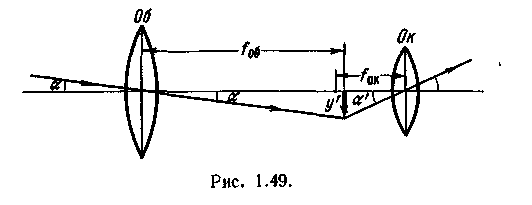
. Зрительная труба (телескоп) предназначена для рассмотрения больших, но удаленных предметов. На рис. 1.49 показано, что зрительная труба состоит из длиннофокусного объектива и короткофокусного окуляра, расположенных на расстоянии порядка Fоб+Fок.
Лучи от крайней точки удаленного предмета пересекают оптическую ось окуляра под некоторым углом а и дают изображение предмета у' в фокальной плоскости. Как видно из рисунка, окуляр превращает большой, но далекий предмет в маленькое, но близкое изображение, не меняя угла зрения а. Полученное изображение рассматривают в окуляр, как в лупу. Общее угловое увеличение зрительной -трубы равно:
^ Для получения значительных увеличений необходимо выполнение условия Для получения значительных увеличений необходимо выполнение условия
Д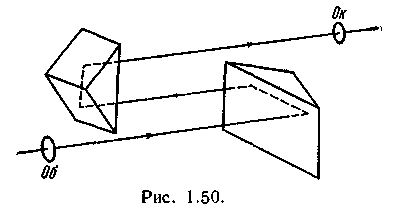 ля уменьшения общих габаритов прибора в бинокле с помощью двух призм полного внутреннего отражения заставляют лучи между объективом и окуляром проходить одно и то же расстояние туда и обратно три раза (рис. 1.50). Для большей компактности обе призмы располагают во взаимно перпендикулярных плоскостях. Бинокль обычно употребляется при наблюдении двумя глазами. Увеличивая расстояние между объективами, мы как бы увеличиваем базу между глазами и добиваемся большей стереоскопичности видения (стереотруба). ля уменьшения общих габаритов прибора в бинокле с помощью двух призм полного внутреннего отражения заставляют лучи между объективом и окуляром проходить одно и то же расстояние туда и обратно три раза (рис. 1.50). Для большей компактности обе призмы располагают во взаимно перпендикулярных плоскостях. Бинокль обычно употребляется при наблюдении двумя глазами. Увеличивая расстояние между объективами, мы как бы увеличиваем базу между глазами и добиваемся большей стереоскопичности видения (стереотруба).
Трудности в изготовлении однородных и точно отшлифованных больших линз приводят к тому, что в астрономических телескопах в качестве объектива широко применяют зеркала.
2. Интерференция световых волн.Когерентность Временная и пространственная когерентность. Способы наблюдения интерференции света. Классические интерференционные опыты: бипризма Френеля, бизеркала Френеля, опыт Юнга, интерференция в тонких пленках, кольца Ньютона. Интерферометры. Многолучевая интерференция. Просветленная оптика и другие практические применения интерференции.
Интерференция световых волн. Когерентность волн.
И
нтерференцией света называется наложение двух или более волн, при котором происходит пространственное перераспределение интенсивности света, наблюдаемое в виде темных и светлых полос.
Возникновение интерференции связано, во-первых, с тем, что для векторов напряженности электрических полей, описывающих электромагнитные волны, выполняется принцип суперпозиции. Так при наложении двух волн, каждая из которых создает в точке наблюдения соответственно электрические поля напряженностью E1 и E2, результирующая напряженность в точке наложения будет равна: Ep = E1 + E2 (1)
Возникновение интерференции связано с тем, что все регистрирующие приборы, в том числе и человеческий глаз, регистрируют не величину напряженности электрического поля, а величину усредненного по времени потока энергии волны, которая характеризуется интенсивностью света (I), равной квадрату амплитуды напряженности электрического поля волны E0: I = E02 (2)
При наложении нескольких волн интерференция наблюдается далеко не в каждом случае. Термин когерентность волн характеризует способность волн при наложении интерферировать. Волны называются когерентными, если при их наложении возникает интерференционная картина и некогерентными, если при их наложении интенсивности волн суммируются и интерференционная картина не возникает. Волны когерентны, если разность фаз между ними остается постоянной во время наблюдения. Для некогерентных волн разность фаз между ними хаотически изменяется во времени.
Если колебания возбуждаемые волной в достаточно близких точках псевдоволновой поверхности оказываются когерентными, то такая когерентность называется пространственной.
Фаза колебания при переходе от одной точки псевдоволновой поверхности к другой изменяется беспорядочным образом. Зведем расстояние рког, при смещении на которое вдоль псевдоволновой поверхности случайное изменение фазы достигает значения л. Колебания в двух точках псевдоволновой поверхности, отстоящих друг от друга на расстояние, меньшее рког, будут при-элизительно когерентными. Расстояние ркОГ называется длиной тространственной когерентности или радиусом когерентности. Из (120.13) следует, что ρ=λφ (120.14)
Схема двухлучевой интерференции(1)
Рассмотрим наложение двух световых волн, идущих от двух источников S1 и S2, в точку Р (см.рис.1). Волны будем полагать монохроматическими и плоскими. Тогда выражения для напряженностей электрического поля двух волн можно записать в виде: E1 = E10 cos(ωt – kz), E2 = E20cos(ω1t – k1z1) (3)
Где Е10 и Е20 - амплитуды первой и второй волн, ω и ω1 - циклические частоты первой и второй волн, k и k1 - волновые числа первой и второй волн (k = 2π/λ,здесь λ -длина волны), z и z1 - расстояния пройденные волнами от источников до точки наблюдения , t - время в момент наложения волн.

Рис.1- Схема двухлучевой интерференции.
Обозначив фазы двух волн, т.е. аргументы периодической функции (в данном случае косинуса), описывающей волны, через φ и φ1 соответственно, можно записать, что разность фаз двух волн равна: ∆φ = φ – φ1 = (ω – ω1)t – kz – k1 z1 . (4)
Из этого выражения видно, что условие когерентности, т.е. постоянство разности фаз во времени, может выполняться лишь для волн с одинаковыми частотами (ω = ω1).
Циклическая частота однозначно связана с волновым числом k = ω/v , (где v - фазовая скорость света в среде - величина для когерентных волн разность фаз определяется геометрической разностью хода волн от источников до точки наложения волн (∆):
∆φ = k (z – z1) = k ∆ . (5)
Волновое число в среде (kc) пропорционально показателю преломления среды: kc = k n, (6)где k - волновое число в вакууме.
Оптическую разность хода (∆), т.е. разность оптических длин путей двух волн ( L 01 и L02 ): ∆φ = k (Lo1- Lo2 ) = k ∆ (7)
Оптическая длина пути волны, прошедшей несколько различных сред (см. рис.2), находится как сумма произведений показателя преломления среды (n 1) на геометрическое расстояние, пройденное волной в данной среде (z1): L0 = n1 z1 + n2 z2 + ... + n1 z1 +... (8)
Оптической длиной пути световой волны называется произведение геометрической длины пути (z1) световой волны в среде на абсолютный показатель преломления (n1) данной среды: Loпт = zi · ni
Зеркала Френеля.
Д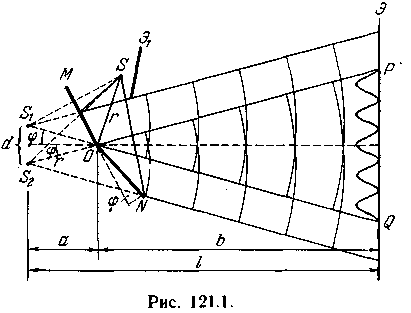 ва плоских соприкасающихся зеркала ОМ и ONрасполагаются так, что их отражающие поверхности образуют угол, близкий к л (рис. 121.1). Соответственно угол ф на рисунке очень мал. Параллельно линии пересечения зеркал О на расстоянии г от нее помещается прямолинейный источник света S (например, узкая светящаяся щель). Зеркала отбрасывают на экран Э две цилиндрические когерентные волны, распространяющиеся так, как если бы они исходили из мнимых источников Si и Si. Непрозрачный экран Э преграждает свету путь от источника S к экрану Э. ва плоских соприкасающихся зеркала ОМ и ONрасполагаются так, что их отражающие поверхности образуют угол, близкий к л (рис. 121.1). Соответственно угол ф на рисунке очень мал. Параллельно линии пересечения зеркал О на расстоянии г от нее помещается прямолинейный источник света S (например, узкая светящаяся щель). Зеркала отбрасывают на экран Э две цилиндрические когерентные волны, распространяющиеся так, как если бы они исходили из мнимых источников Si и Si. Непрозрачный экран Э преграждает свету путь от источника S к экрану Э.
Луч OQпредставляет собой отражение луча SOот зеркала ОМ, луч ОР — отражение луча SOот зеркала ON. Легко сообразить, что угол между лучами ОР и OQравен 2ф. Поскольку S и Si расположены относительно ОМ симметрично, длина отрезка OSi равна OS, т. е. г. Аналогичные рассуждения приводят к тому же результату для отрезка OS2. Таким образом, расстояние между источниками Si и S2 равно
Из рис. 121.1 видно, что Следовательно, где ь — расстояние от линии пересечения зеркал О до Ширина интерференционной полосы:
(121.1)
Максимальное число интерференционных полос, которое можно наблюдать с помощью зеркал Френеля при данных параметрах схемы:
(121.2)
20.10).
Бипризма Френеля.
И зготовленные из одного куска стекла две призмы с малым преломляющим углом д имеют одну общую грань (рис. 121.2). Параллельно этой грани на расстоянии а от нее располагаетсяпрямолинейный источник света S. зготовленные из одного куска стекла две призмы с малым преломляющим углом д имеют одну общую грань (рис. 121.2). Параллельно этой грани на расстоянии а от нее располагаетсяпрямолинейный источник света S.
Можно показать, что в случае, когда преломляющий луч призмы очень мал и углы падения лучей на грань призмы не очень велики, все лучи отклоняются призмой на практически одинаковый угол, равный
(п — показатель преломления призмы). Угол падения лучей на бипризму невелик. Поэтому все лучи отклоняются каждой из половин бипризмы на одинаковый угол. В результате образуются две когерентные цилиндрические волны, исходящие из мнимых источников Si и S2, лежащих в одной плоскости с S. Расстояниемежду источниками равно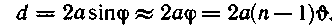
Максимальное число наблюдаемых полос
(121.4) Расстояние от источников до экрана
Двухлучевая интерференция
Пусть световые волны, испускаемые источниками S1 и S2, являются монохроматическими с одинаковой и постоянной частотой ω, а в рассматриваемой точке наблюдения Р (см.рис.1) оба вектора E1 и E2 параллельны друг другу, тогда их можно считать скалярными величинами и записать результирующую напряженность электрического поля в точке Р в соответствии с принципом суперпозиции (1) в следующем виде: Ер = Е10 cos (ωt – kz1) + E20cos (ωt – kz2) (9)
Для сложения двух гармонических функций удобно пользоваться методом фазовых диаграмм. При этом напряженность электрического поля волны представляется как проекция на некоторую ось 00' вектора по величине равного амплитуде волны, повернутого относительно этой оси на угол равный фазе волны (см. рис. За).
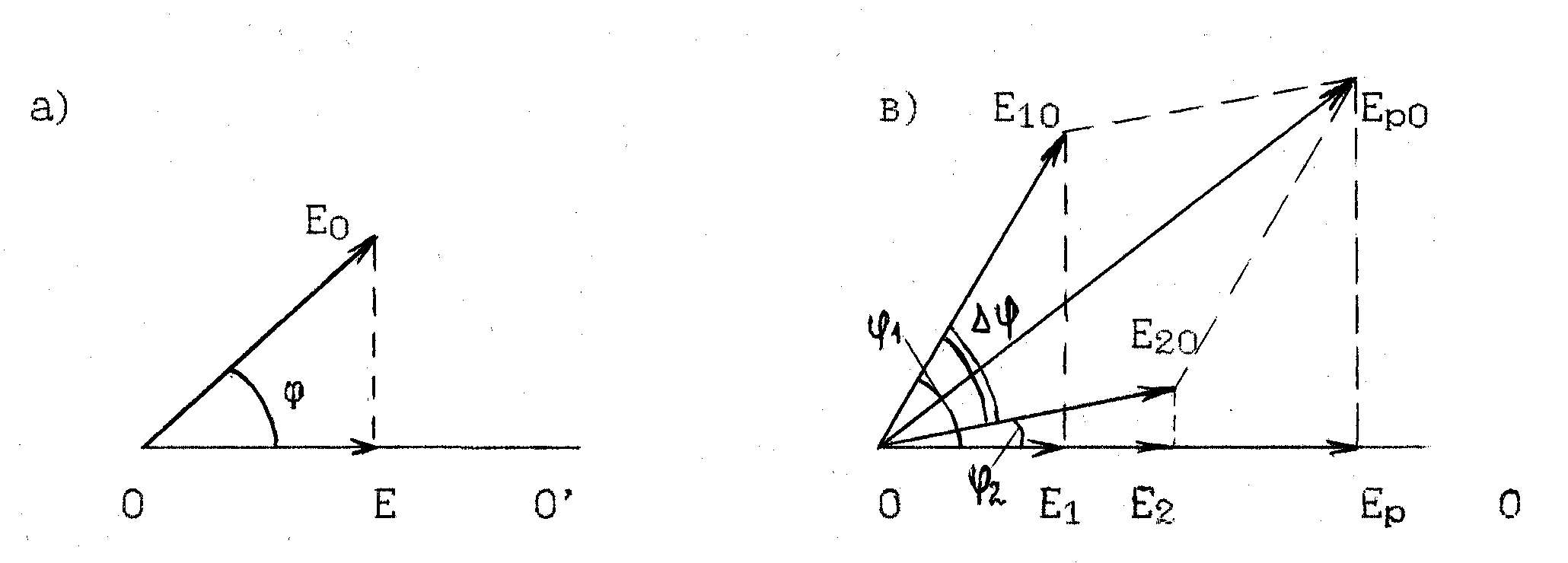
Рис.3. Фазовые диаграммы одной волны - (а) и двух - (в), налагающихся волн.
Если координата точки наблюдения и положение источника неизменны, то во время наблюдения расстояние z постоянно, и фаза волны будет зависеть только от времени. С течением времени фаза волны будет расти и вектор Е0 будет вращаться с частотой ω относительно выбранной оси. Проекция вектора при этом будет изменяться по гармоническому закону в соответствии с уравнением:
E(t) = Eo cos (ωt + φ ) (10)
где φ - начальная фаза волны, зависящая от z.
При сложении двух волн, каждая из них представляется проекцией соответствующего вектора на выбранную ось, и результирующая волна равна сумме проекций (см. рис.Зв). Результат не изменится, если сначала сложить вектора, а затем взять проекцию.
Так как для нахождения интенсивности достаточно знать амплитуду результирующей волны (см. формулу 2), то после сложения векторов можно и не искать проекцию результирующего вектора на ось, а ограничится найденой амплитудой результирующей волны (Ер0) и определить интенсивность света в точке наложения.
Из рис. Зв видно, что амплитуда результирующего вектора не зависит от фаз налагающихся волн (фазы волн изменяются с течением времени, что приводит к синхронному вращению векторов), а зависит лишь от разности фаз (∆φ) между налагающимися волнами (на рисунке разность фаз - это угол между векторами Е10 и E20) и от амплитуд этих волн.
Применяя теорему косинусов (см. рис.Зв), можно записать:
Еp02 = Е102 + E202 + 2E10 2 E202cos ∆φ (11)
Так как интенсивность света (I) пропорциональна квадрату амплитуды колебаний вектора напряжённости электрического поля, то   (12) (12)
Последнее слагаемое называют интерференционным членом. В тех
точках пространства, для которых cos ∆φ > 0 , результирующая интенсивность (Ip) будет превышать сумму интенсивностей I1 и I2 . В точках, для которых cos ∆φ < 0 , Ip будет меньше I1 + I2.
Таким образом, при наложении когерентных световых волн происходит перераспределение светового потока в пространстве, в результате чего в одних местах возникают максимумы, а в других - минимумы интенсивности.
1).Результирующая интенсивности - Ip при наложении двух когерентных волн максимальна
 , если ∆φ = 2πm. (13) , если ∆φ = 2πm. (13)
Сравнивая (7) и (13), можно сказать, что при интерференции наблюдается максимум интенсивности, если оптическая разность хода двух интерферирующих волн равна целому числу длин волн
∆ = тλ (14)
где m - называется порядком интерференции и показывает, сколько длин волн укладывается в оптической разности хода (m = 0, ±1, ±2,...).
2).Результирующая интенсивность I - минимальна.
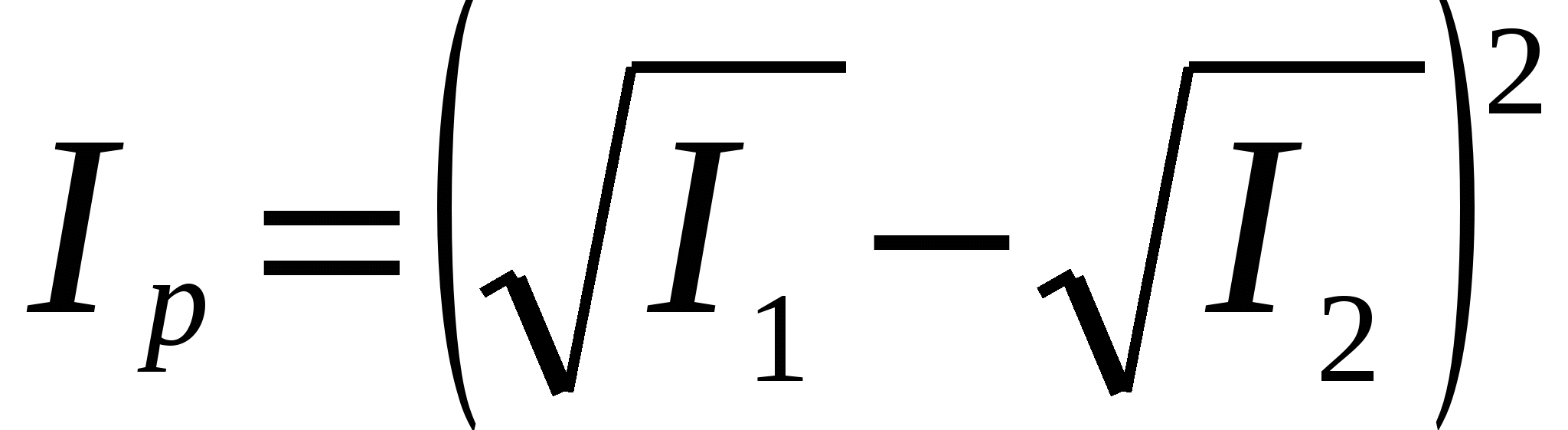 , если ∆φ = (2m +l) π, (15) , если ∆φ = (2m +l) π, (15)
где - m = 0, ±1, ±2,...
Т.е. минимум интенсивности наблюдается, если оптическая разность хода равна нечетному числу полуволн:
∆ = (2m +1) λ/2. (16)
Для некогерентных волн ∆φ непрерывно изменяется, результирующая интенсивность Iр = 2I1 .
Максимальная величина оптической разности хода двух волн, полученных делением одной волны на части, при которой еще наблюдается интерференция, называется длиной когерентности излучения. Длина когерентности излучения определяется длиной волны и шириной спектра излучения и равна
LK = λ2/ ∆λ, (I7)
где ∆λ - ширина спектрального интервала в длинах волн, в пределах которого интенсивность излучения отлична от нуля.
Максимальное значение промежутка времени, при котором когерентность ещё сохраняется, называется временем когерентности излучения (tk) .
Длина и время когерентности связаны следующим соотношением: L K = t K V, (18) где V - скорость света.
Опыт Юнга
В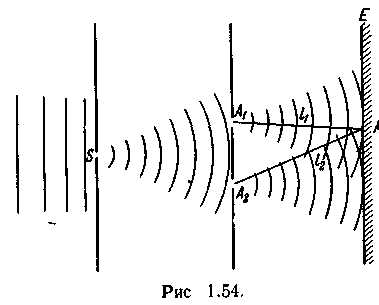 опыте Юнга (рис. 1.54) свет из точечного источника (малое отверстие S) проходит через два равноудаленных отверстия aiи Л2, являющихся как бы двумя когерентными источниками. Интерференционная,картина наблюдается на экране Е, расположенном на некотором расстоянии параллельно AtAz. Усиление и ослабление света в произвольной точке М экрана зависят от разности хода лучей I2-I1. опыте Юнга (рис. 1.54) свет из точечного источника (малое отверстие S) проходит через два равноудаленных отверстия aiи Л2, являющихся как бы двумя когерентными источниками. Интерференционная,картина наблюдается на экране Е, расположенном на некотором расстоянии параллельно AtAz. Усиление и ослабление света в произвольной точке М экрана зависят от разности хода лучей I2-I1.
Зеркала Френеля представляют собой два плоских зеркала, расположенных под углом, близким к 180° друг к другу 1(рис. 1.55). Источник S испускает свет, отражающийся от обоих зеркал и попадающий на экран Е, защищенный от прямого попадания кожухом К.
По законам отражения от плоского зеркала (см. § 7) лучи, отраженные от первого зеркала, как бы исходят из мнимого источника Sltрасположенного симметрично исходному источнику S. Аналогично, лучи, отраженные от второго зеркала, можно рассматривать исходящими из мнимого источника S2, являющегося изображением источника S во втором зеркале. Мнимые источники Sj и Szвзаимно когерентны, и исходящие из них пучки лучей пересекаются и интерферируют в области, заштрихованной на рис. 1.55. Интерференционная картина наблюдается на экране Е, помещенном в эту область, и зависит от разности хода лучей I2-I1.до произвольных точек экрана.
Интерференция в тонких пленках.
При освещении тонкой плёнки или пластинки происходит наложение световых волн, отразившихся от передней и задней поверхностей плёнки. Эти две волны получаются делением волны, идущей от одного источника S (см. рис.4). Для плоскопараллельной пластинки постоянной толщины интерференционная картина наблюдается в фокальной плоскости линзы, собирающей отражённые от верхней и нижней граней пластинки пучки лучей 1 и 2.
Л учи 1 и 2 образуются из падающего на пластинку луча SA. От источника S до точки А между ними разность хода отсутствует. Линия DC, перпендикулярная лучам 1 и 2, представляет собой волновую поверхность, т.е. поверхность постоянной фазы. учи 1 и 2 образуются из падающего на пластинку луча SA. От источника S до точки А между ними разность хода отсутствует. Линия DC, перпендикулярная лучам 1 и 2, представляет собой волновую поверхность, т.е. поверхность постоянной фазы.
Линза не вносит дополнительной разности хода для параллельных лучей, а лишь преобразует плоскую волну в сходящуюся сферическую волну. Поэтому после перпендикуляра DC, опущенного на лучи 1 и 2, до точки наложения лучей Р разность хода между лучами 1 и 2 также не возникает.
Оптическая разность хода между лучами 1 и 2 возникает из-за того, что первый луч прошел, отразившись от границы раздела воздух-среда, отрезок AD в воздухе, а второй луч прошел путь АВС от точки А до точки С в пластинке с показателем преломления n и отразился от границы раздела среда-воздух.
При отражении световой волны от оптически более плотной среды (отражение луча 1 в точке А) фаза отраженной волны изменяется на противоположную (т.е. на π). Это можно представить как возникновение разности хода равной половине длины волны для первого луча. При отражении волны от оптически менее плотной среды (отражение луча 2 в точке В) изменения фазы не происходит, и соответственно разности хода не возникает.
Поэтому колебания в точку С (волновая поверхность DC) приходят оптическими путями: L1 = n(AB + ВС) и L2 = AD + λ/2 . Отсюда можно записать, что оптическая разность хода, возникающая между лучами 1 и 2 от источника S до точки наложения лучей Р будет равна:
∆ = L 1 - L2 = n (АВ + ВС) - (AD + λ /2) = 2nАВ - AD – λ /2 (19)
Отрезки AD и АВ удобнее выразить через толщину пластинки (d) и угол падения луча ( i ) или угол преломления луча (r), используя треугольники ABE и ACD:
из треугольника ABE АВ = d / cos r, ЕВ = d tg r (20)
из треугольника ADC AD = AC sin i, AC = 2EB = 2d tg r,
∆ = 2nd/Cos r – AC Sin i = 2nd /Cos r - 2dtg rsin i = 2nd / Cos r - 2dSin r /Cos r Sin i = 2dCos r (n - Sin r Sin i )
по закону преломления света на границе двух сред Sin i = n Sin r, тогда
Δ = 2d/Cos r (n - nSin2r), умножим левую половину равенства на n\n
Δ= 2d/nCos r.(n2 - n2 Sin2r) ,из тригонометрии знаем, что  , тогда, если , тогда, если  то получим: то получим:
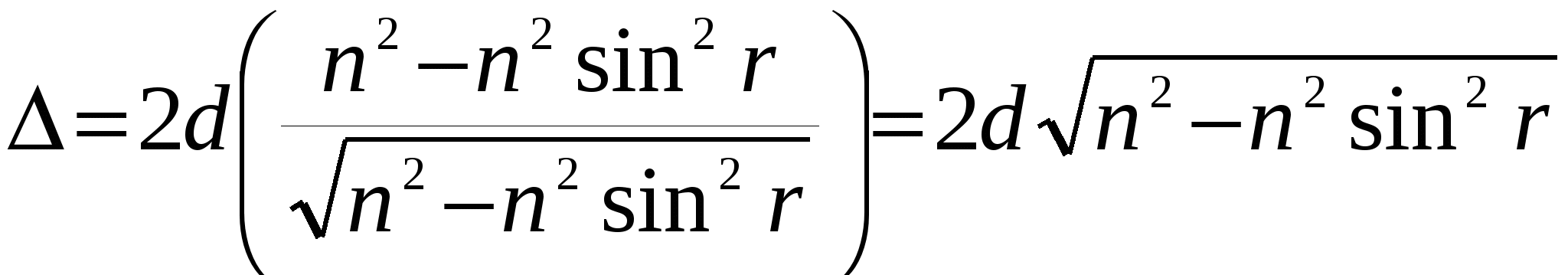 (21) (21)
вспомним, что n · Sin r = Sin i, тогда  , учтём изменение фазы отражённого луча на λ⁄2 и получим: , учтём изменение фазы отражённого луча на λ⁄2 и получим: 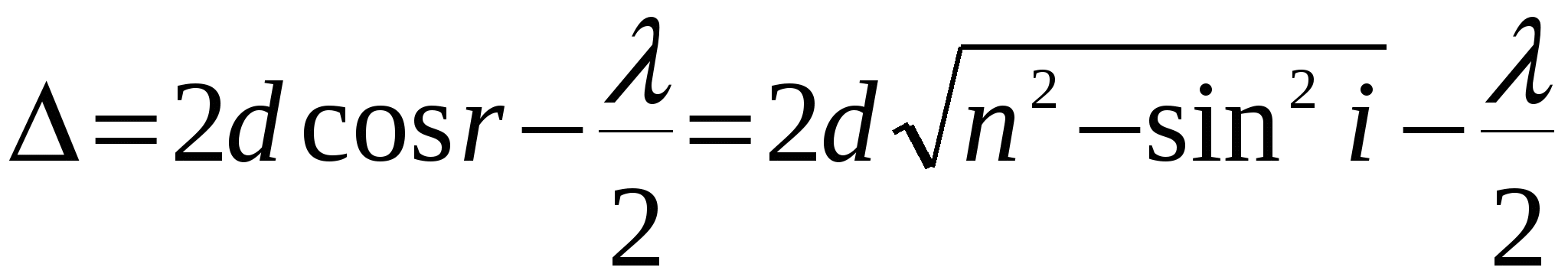 (22) (22)
Колеца Ньютона.Определения радиуса кривизны линзы
Интерференционные полосы равной толщины в тонкой пленке, т.е. темные или светлые полосы соответствующие постоянному значению толщины пленки (d), можно наблюдать в воздушной прослойке между соприкасающимися друг с другом плоской поверхностью пластинки и выпуклой сферической поверхностью линзы (см. рис.5).
При этом толщина воздушной прослойки постепенно увеличивается от центра линзы к ее краям. При нормальном (перпендикулярном поверхности) падении света полосы равной толщины имеют вид концентрических окружностей, которые получили название колец Ньютона.
Если на линзу падает пучок монохроматического света, то световые волны, отражённые от верхней и нижней границ воздушной прослойки, интерферируют между собой.
Т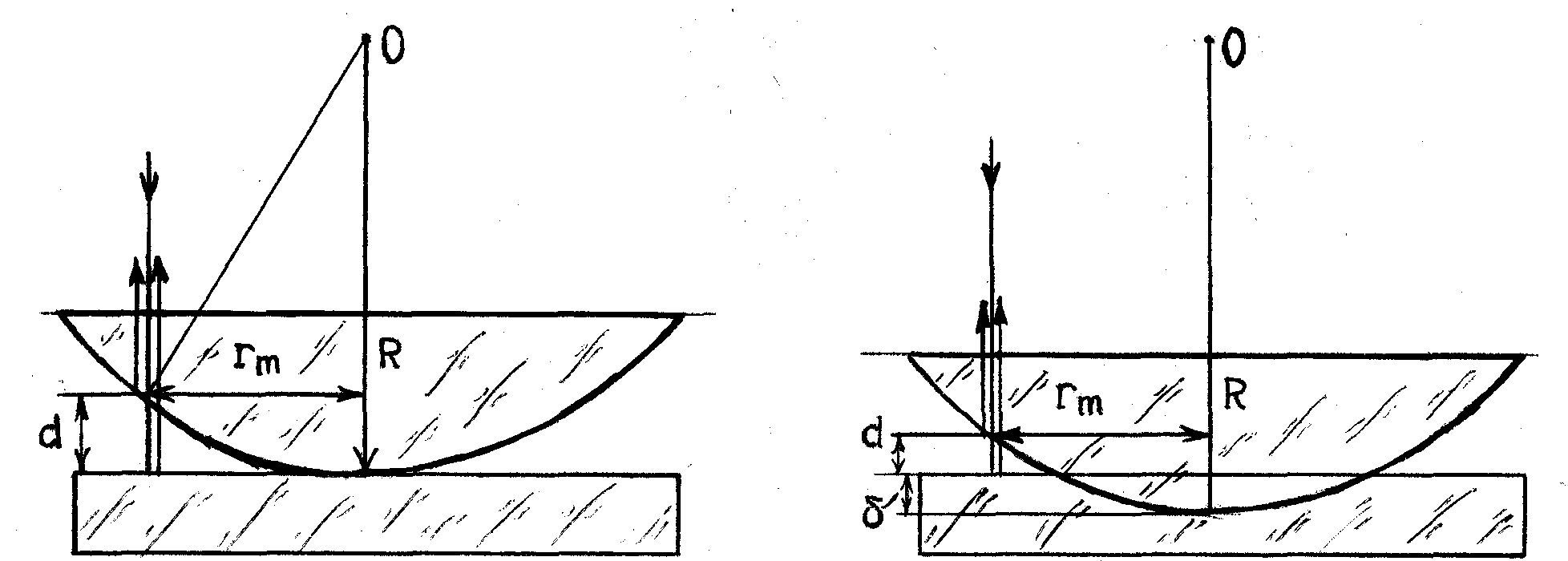 ак как, в отличии от выше приведённого примера, отражение световой волны происходит в точке В от раздела среды воздух-стекло, а не стекло-воздух, как на рис.4,то λ/2 добавляется к слагаемому L1 и формула (19), в начальной её части приобретёт вид: ак как, в отличии от выше приведённого примера, отражение световой волны происходит в точке В от раздела среды воздух-стекло, а не стекло-воздух, как на рис.4,то λ/2 добавляется к слагаемому L1 и формула (19), в начальной её части приобретёт вид:
∆ = L1- L2 = (АВ + ВС + λ/2) - AD = 2d + λ/2
То есть, оптическая разность хода, в этом случае равна удвоенной толщине воздушного зазора (2d) ( показатель преломления воздуха n = 1).
В итоге получим: ∆ = 2d + λ/2 (23)
|
 Скачать 1.22 Mb.
Скачать 1.22 Mb.
 ва плоских соприкасающихся зеркала ОМ и ONрасполагаются так, что их отражающие поверхности образуют угол, близкий к л (рис. 121.1). Соответственно угол ф на рисунке очень мал. Параллельно линии пересечения зеркал О на расстоянии г от нее помещается прямолинейный источник света S (например, узкая светящаяся щель). Зеркала отбрасывают на экран Э две цилиндрические когерентные волны, распространяющиеся так, как если бы они исходили из мнимых источников Si и Si. Непрозрачный экран Э преграждает свету путь от источника S к экрану Э.
ва плоских соприкасающихся зеркала ОМ и ONрасполагаются так, что их отражающие поверхности образуют угол, близкий к л (рис. 121.1). Соответственно угол ф на рисунке очень мал. Параллельно линии пересечения зеркал О на расстоянии г от нее помещается прямолинейный источник света S (например, узкая светящаяся щель). Зеркала отбрасывают на экран Э две цилиндрические когерентные волны, распространяющиеся так, как если бы они исходили из мнимых источников Si и Si. Непрозрачный экран Э преграждает свету путь от источника S к экрану Э. зготовленные из одного куска стекла две призмы с малым преломляющим углом д имеют одну общую грань (рис. 121.2). Параллельно этой грани на расстоянии а от нее располагаетсяпрямолинейный источник света S.
зготовленные из одного куска стекла две призмы с малым преломляющим углом д имеют одну общую грань (рис. 121.2). Параллельно этой грани на расстоянии а от нее располагаетсяпрямолинейный источник света S.
 опыте Юнга (рис. 1.54) свет из точечного источника (малое отверстие S) проходит через два равноудаленных отверстия aiи Л2, являющихся как бы двумя когерентными источниками. Интерференционная,картина наблюдается на экране Е, расположенном на некотором расстоянии параллельно AtAz. Усиление и ослабление света в произвольной точке М экрана зависят от разности хода лучей I2-I1.
опыте Юнга (рис. 1.54) свет из точечного источника (малое отверстие S) проходит через два равноудаленных отверстия aiи Л2, являющихся как бы двумя когерентными источниками. Интерференционная,картина наблюдается на экране Е, расположенном на некотором расстоянии параллельно AtAz. Усиление и ослабление света в произвольной точке М экрана зависят от разности хода лучей I2-I1. учи 1 и 2 образуются из падающего на пластинку луча SA. От источника S до точки А между ними разность хода отсутствует. Линия DC, перпендикулярная лучам 1 и 2, представляет собой волновую поверхность, т.е. поверхность постоянной фазы.
учи 1 и 2 образуются из падающего на пластинку луча SA. От источника S до точки А между ними разность хода отсутствует. Линия DC, перпендикулярная лучам 1 и 2, представляет собой волновую поверхность, т.е. поверхность постоянной фазы. 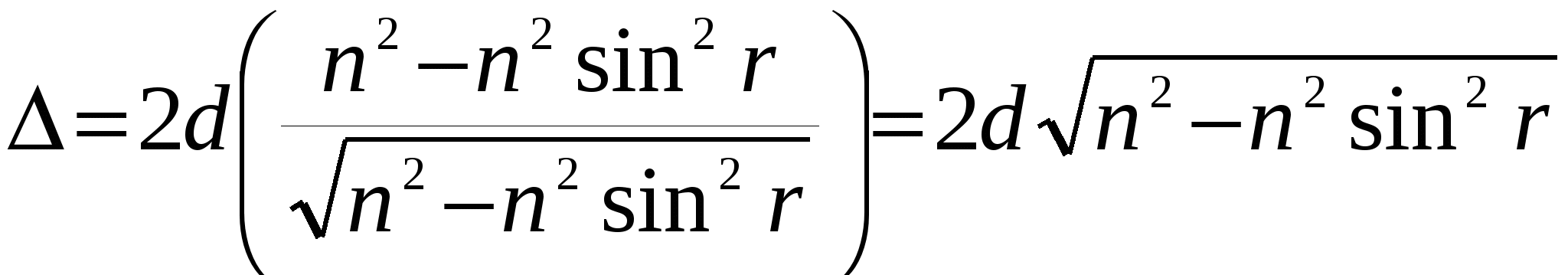 (21)
(21) ак как, в отличии от выше приведённого примера, отражение световой волны происходит в точке В от раздела среды воздух-стекло, а не стекло-воздух, как на рис.4,то λ/2 добавляется к слагаемому L1 и формула (19), в начальной её части приобретёт вид:
ак как, в отличии от выше приведённого примера, отражение световой волны происходит в точке В от раздела среды воздух-стекло, а не стекло-воздух, как на рис.4,то λ/2 добавляется к слагаемому L1 и формула (19), в начальной её части приобретёт вид:



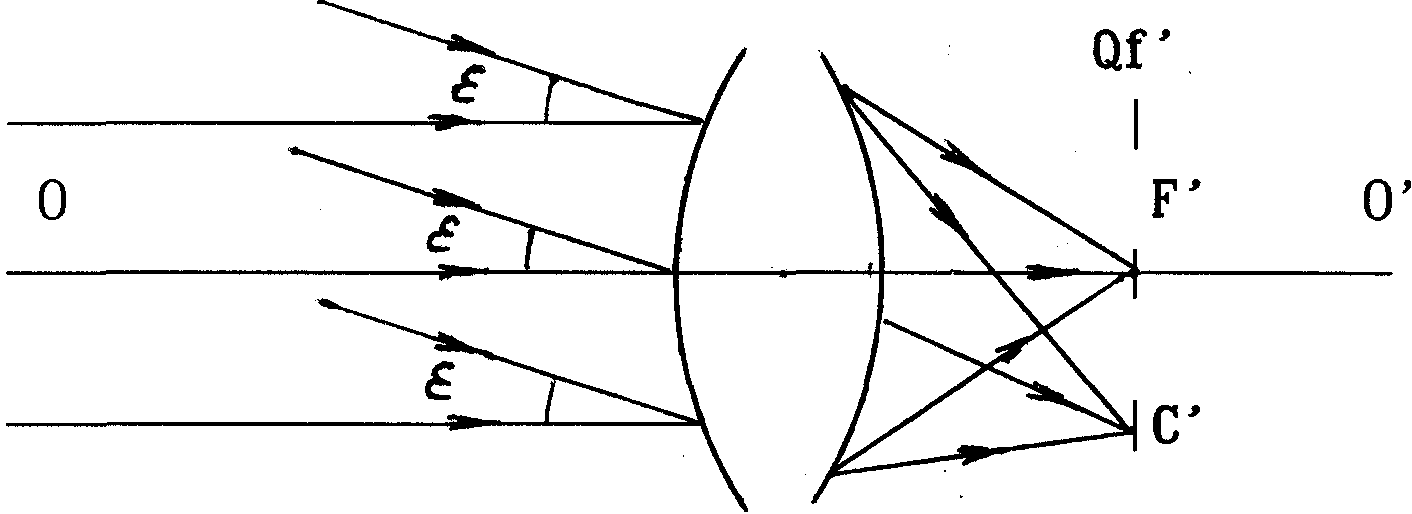




 асчеты, которых мы не приводим, дают, что в случае тонкой линзы главные плоскости Я и Я' можно считать совпадающими и проходящими через центр линзы О (рис. 117.1). Для фокусных расстояний тонкой линзы получается выражение
асчеты, которых мы не приводим, дают, что в случае тонкой линзы главные плоскости Я и Я' можно считать совпадающими и проходящими через центр линзы О (рис. 117.1). Для фокусных расстояний тонкой линзы получается выражение 
 де F— переднее фокусное расстояние хрусталика.
де F— переднее фокусное расстояние хрусталика.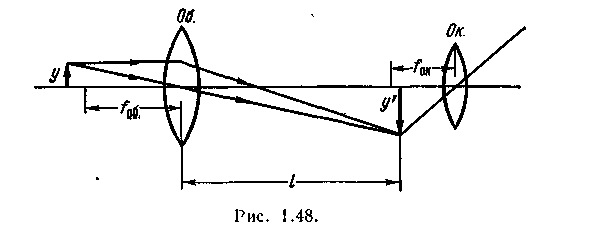 ассматриваемый предмет у помещают на расстояние, несколько превышающее главное фокусное расстояние объектива FОб.
ассматриваемый предмет у помещают на расстояние, несколько превышающее главное фокусное расстояние объектива FОб.
 ля уменьшения общих габаритов прибора в бинокле с помощью двух призм полного внутреннего отражения заставляют лучи между объективом и окуляром проходить одно и то же расстояние туда и обратно три раза (рис. 1.50). Для большей компактности обе призмы располагают во взаимно перпендикулярных плоскостях. Бинокль обычно употребляется при наблюдении двумя глазами. Увеличивая расстояние между объективами, мы как бы увеличиваем базу между глазами и добиваемся большей стереоскопичности видения (стереотруба).
ля уменьшения общих габаритов прибора в бинокле с помощью двух призм полного внутреннего отражения заставляют лучи между объективом и окуляром проходить одно и то же расстояние туда и обратно три раза (рис. 1.50). Для большей компактности обе призмы располагают во взаимно перпендикулярных плоскостях. Бинокль обычно употребляется при наблюдении двумя глазами. Увеличивая расстояние между объективами, мы как бы увеличиваем базу между глазами и добиваемся большей стереоскопичности видения (стереотруба).