Шпаргалка по оптике. 1. Геометрическая оптика

• Название: 1. Геометрическая оптика
• Анкор: Шпаргалка по оптике.doc
• Дата: 16.10.2017
• Размер: 1.22 Mb.
• Имя файла: Шпаргалка по оптике.doc
• Тип: Документы; #9430
• Категория: Физика
• страница: 3 из 7

Освещенность. Степень освещенности некоторой поверхности падающим на нее светом характеризуется величиной

(114.5)

называемой освещенностью (— световой поток, па­дающий на элемент поверхности).

Единицей освещенности является люкс (лк), равный осве­щенности, создаваемой потоком в 1 лм, равномерно распределен­ным по поверхности площади в 1 м²:

(114.6)

Освещенность Е, создаваемую точечным источником, можно выразить через силу света /, расстояние г от поверхности до источ­ника и угол а между нормалью к поверхности п и направлением на источник. На площадку dS(gnc. 114.1) падает поток=

—, заключенный в пределах телесного угла, опирающе­гося на Угол равен Следовательно, Разделив этот поток на dS, получим

(114.7)

С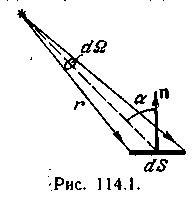
ветимость. Протяженный источник света можно охарактери­зовать светимостью М различных его участков, под кото­рой понимается световой поток, испускаемый единицей площади наружу по всем направлениям (в пределах значений О от 0 до л/2; Ф — угол, образуе­мый данным направлением с внешней нор­малью к поверхности):

(114.8)

(— поток, испускаемый наружу по всем направлениям элементом поверхностиис­ точника).

Светимость может возникнуть за счет отражения поверхностью падающего на нее света. Тогда подв формуле (114.8) следует

понимать поток, отраженный элементом поверхностипо всем направлениям.

Единицей светимости является люмен на квадратный метр (лм/м²).

Яркость. Светимость характеризует излучение (или отраже­ние) света данным местом поверхности по всем направлениям. Для характеристики излучения (отражения) света в заданном направ­лении служит яркость L. Направление можно задать полярным углом О (отсчитываемым от внешней нормали п к излучающей пло­щадке ,) и азимутальным углом ф. Яркость определяется как отношение силы света элементарной поверхностив данном на­правлении к проекции площадкина плоскость, перпендикуляр­ную к взятому направлению.

Рассмотрим элементарный телесный угол, опирающийся на светящуюся площадку и ориентированный в направлении

(*, ф) (рис. 114.2). Сила света площадкив данном направле­нии согласно определению (114.1) равна — световой поток, распространяющийся в пределах углаПроек­цией AS на плоскость, перпендикулярную к направлению () (на рис. 114.2 след этой плоскости изображен пунктиром), будет Следовательно, яркость равна

(114.9)

В о0щем случае яркость различна для разных направлений: . Как и светимость, яркость может быть использована

для характеристики поверхности, отражающей падающий на нг< свет.

Согласно формуле (114.9) поток, излучаемый площадкойи пределах телесного углапо направлению, определяемому о и ф, равен (114.10)

Источники, яркость которых одинакова по всем направлениям (L = const), называются ламбертовскими (подчиняющимися закону Ламберта) или косинусны м и (поток, посылаемый элементом поверхности такого источника, пропорционален соз Ф). Строго следует закону Ламберта только абсолютно черное тело!

С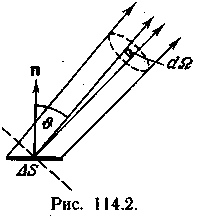ветимость М и яркость L ламбертовско го источника связаны простым соотношением. Чтобы найти его, подставим в (114.10) и проинтегрируем полученное выражение по ср в пределах от 0 до 2я и по ftот 0 до я/2, учтя, что_{. В} результате мы найдем полный световой поток, испускаемый элементом поверхностиламбертовского источника наружу по всем на­правлениям: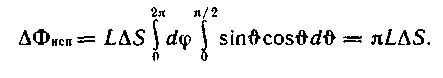



Разделив этот поток на AS, получим светимость. Таким образом, для ламбертовского источника

(114.11)

Единицей яркости служит кандела на квадратный метр (кд/м²). Яркостью в 1 кд/м² обладает равномерно светя­щаяся плоская поверхность в направлении нормали к ней, если в этом направлении сила света одного квадратного метра поверхно­сти равна одной канделе.

Тепловое излучение тел.

Тепловым излучением тел называется электромагнитное излучение, возникающее за счет той части внутренней энергии тела, которая связана с тепловым движением его частиц.

Основными характеристиками теплового излучения тел нагретых до температуры T являются:

1. Спектральная плотность энергетической светимости r(, Т) - количество энергии, излучаемое единицей поверхности тела, в единицу времени в единичном интервале длин волн (вблизи рассматриваемой длины волны ). Эта величина зависит от температуры тела, длины волны испускаемого света, а также от природы и состояния поверхности излучающего тела. В системе СИ r(, T) имеет размерность [Вт/м³].

2. Энергетическая светимость R(T) - количество энергии, излучаемой в единицу времени с единицы поверхности тела, во всем интервале длин волн. Зависит от температуры, природы излучающего тела и состояния его поверхности.

Энергетическая светимость R(T) связана со спектральной плотностью энергетической светимости r(, T) следующим образом:

(1).

Размерность энергетической светимости в системе СИ - [Вт/м²]

3. Все тела не только излучают, но и поглощают падающие на их поверхность электромагнитные волны. Для определения поглощательной способности тел по отношению к электромагнитным волнам определенной длины волны вводится понятие коэффициента монохроматического поглощения - отношение величины поглощенной поверхностью тела энергии монохроматической волны к величине энергии падающей монохроматической волны:

(2).

Коэффициент монохроматического поглощения является безразмерной величиной, зависящей от температуры и длины волны. Он показывает, какая доля энергии падающей монохроматической волны поглощается поверхностью тела. Величина (,T) может принимать значения от 0 до 1.
Равновесное тепловое излучение. Абсолютно черное тело. Закон Кирхгофа.
Если мы создадим некоторую оболочку, непрозрачную для электромагнитных волн, и будем поддерживать ее при постоянной температуре, то внутри ее установится равновесие. Вся энергия, излучаемая внутренней поверхностью оболочки, будет ею же и поглощаться. Излучение в адиабатически замкнутой системе (не обменивающейся теплотой с внешней средой) называется равновесным. Если создать маленькое отверстие в стенке оболочки, состояние равновесия измениться слабо и выходящее из полости излучение будет соответствовать равновесному излучению.

Если в такое отверстие направить луч, то после многократных отражений и поглощения на стенках полости он не сможет выйти обратно наружу. Это значит, что для такого отверстия коэффициент поглощения (, T) = 1.

Рассмотренная замкнутая полость с небольшим отверстием служит одной из моделей абсолютно черного тела.

Абсолютно черным телом называется тело, которое поглощает все падающее на него излучение независимо от направления падающего излучения, его спектрального состава и поляризации (ничего не отражая и не пропуская).

Для абсолютно черного тела, спектральная плотность энергетической светимости является некоторой универсальной функцией длины волны и температуры f(,T) и не зависит от его природы.

Все тела в природе частично отражают падающее на их поверхность излучение и поэтому не относятся к абсолютно черным телам. Если коэффициент монохроматического поглощения тела одинаков длявсех длин волн и меньше единицы ((, T) = _Т = const<1), то такое тело называетсясерым. Коэффициент монохроматического поглощения серого тела зависит только от температуры тела, его природы и состояния его поверхности.

Кирхгофом было показано, что для всех тел, независимо от их природы, отношение спектральной плотности энергетической светимости к коэффициенту монохроматического поглощения является той же универсальной функцией длины волны и температуры f(,T), что и спектральная плотность энергетической светимости абсолютно черного тела:

₍₃₎

Уравнение (3) представляет собой закон Кирхгофа.

Закон Кирхгофа можно сформулировать таким образом: для всех тел системы, находящейся в термодинамическом равновесии, отношение спектральной плотности энергетической светимости к коэффициентумонохроматического поглощения не зависит от природы тела и является одинаковой для всех тел функцией, зависящей от длины волны  и температуры Т.

Из вышесказанного и формулы (3) ясно, что при данной температуре сильнее излучают те серые тела, которые обладают большим коэффициентом поглощения. Наиболее сильно излучают абсолютно черные тела.

Законы излучения абсолютно черного тела
Формула Планка.

Выражение для спектральной плотности энергетической светимости абсолютно черного тела было получено впервые немецким физиком М. Планком. Согласно квантовой гипотезе Планка испускание энергии электромагнитных волн атомами вещества может происходить только отдельными "порциями" - квантами. При этом энергия кванта света пропорциональна его частоте:

(4).

Постоянная h была названа постоянной Планка, c-скорость света в вакууме. На основании этой гипотезы, используя статистические методы, он получил следующую формулу: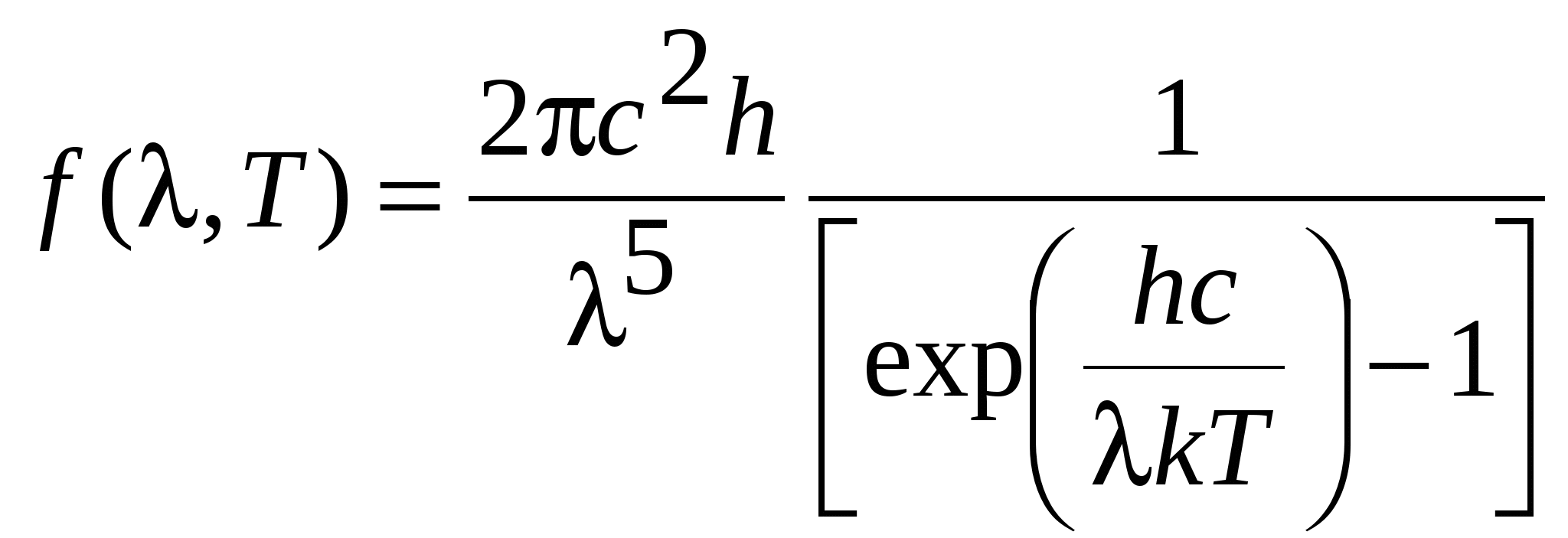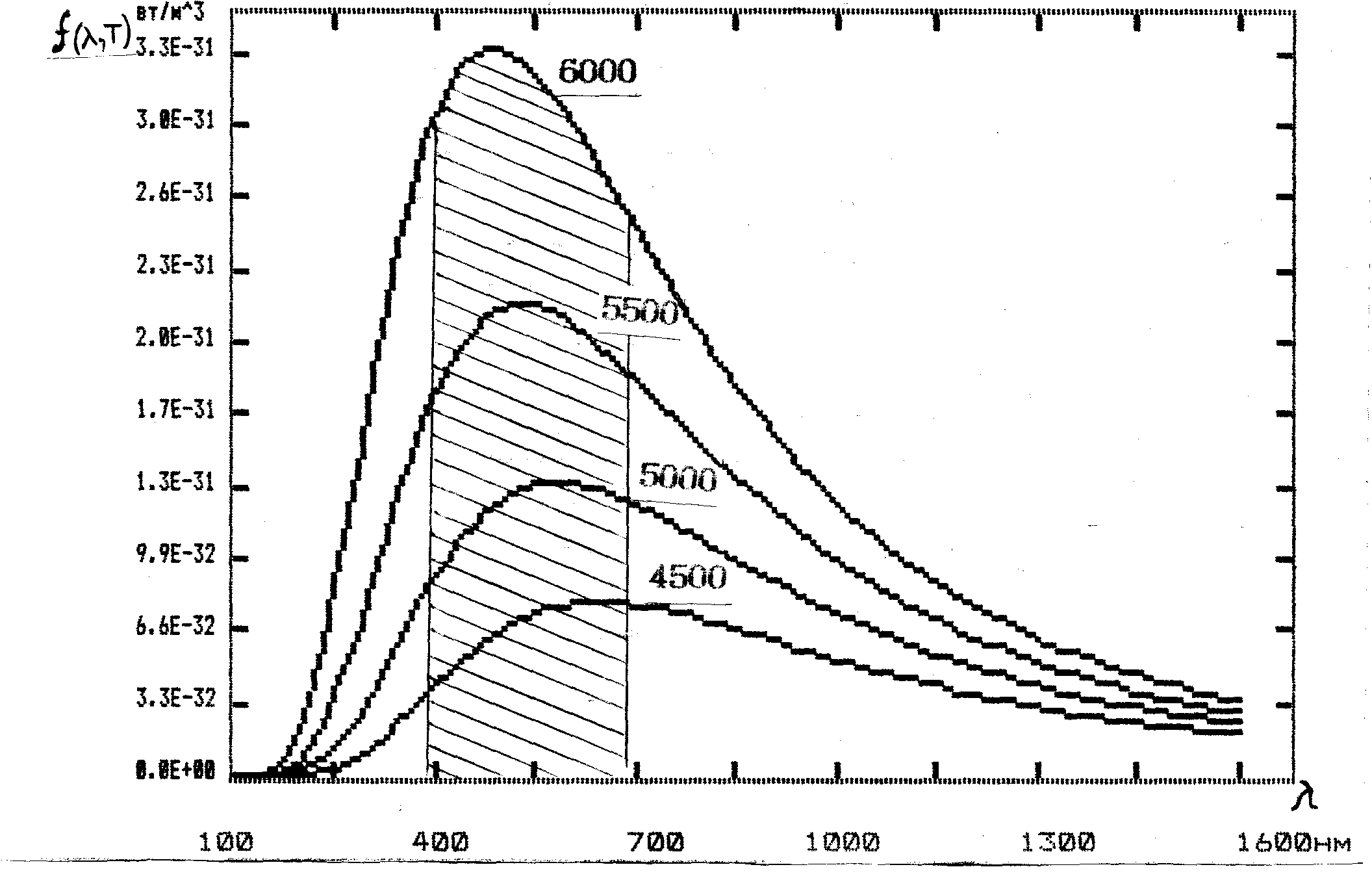

(5),

где: k-постоянная Больцмана.


Рис.1 Зависимость спектральной плотности энергетической светимости абсолютно черного тела от длины волны

На рис.1 представлены графики f(, T) для различных температур. Формула (5) хорошо согласуется с экспериментальными данными во всем интервале наблюдаемых длин волн и температур и называется формулой Планка.

Основные законы излучения абсолютно черного тела можно получить из формулы Планка. Однако многие из них получены на основе экспериментальных данных, а также представлений классической физики еще до открытия Планком своей формулы. Поэтому эти закономерности носят имя ученых, открывших их, и формулируются в виде законов.
Закон смещения Вина.

Из рис.1 видно, что максимум спектральной плотности энергетической светимости с ростом температуры смещается в сторону более коротких волн. Чтобы найти закон смещения данного максимума, необходимо продифференцировать выражение (5) по  и приравнять производную к нулю. Из полученного уравнения можно найти длину волны, соответствующую максимуму спектральной плотности энергетической светимости абсолютно черного тела как функцию температуры:

(6),

где b - постоянная Вина , _max - длина волны, соответствующая максимальному значению спектральной плотности энергетической светимости

(7)
Закон Вина можно сформулировать следующим образом: Длина волны,соответствующая максимальному значению спектральной плотности энергетической светимости абсолютно черного тела, обратно пропорциональна его температуре.

Закон Рэлея-Джинса.

(9).

Эта формула, получившая название формулы Рэлея-Джинса, хорошо описывает тепловое излучение абсолютно черного тела на длинах волн, удовлетворяющих условию:

(10).

Рэлей и Джинс получили эту формулу до открытия Планка, основываясь на представлении о непрерывном характере испускания электромагнитных волн и на законе о равномерном распределении энергии по степеням свободы.

Формула Рэлея-Джинса верна для длинных волн и совершенно не применима для коротких.

Закон Стефана – Больцмана

В 1879 г. Стефан из анализа экспериментальных результатов, а в 1884г. Больцман из термодинамических представлений получили зависимость энергетической светимости абсолютно черного тела от температуры:

R(T)=σT⁴ (11),

где постоянная σ=5.67 10^-8 Вт/(м² К⁴) - постоянная Стефана-Больцмана.

Из выражения (11) можно сформулировать закон Стефана-Больцмана:

Э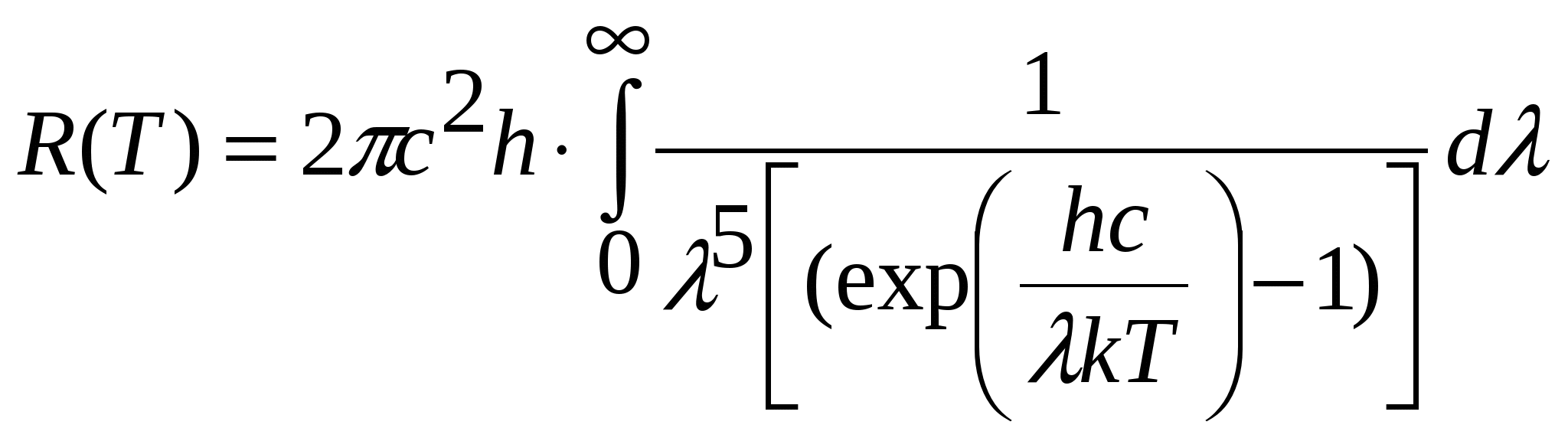нергетическая светимость абсолютно чёрного тела пропорциональна четвёртой степени его термодинамической температуры.

Формулу (11) можно получить, используя формулу Планка (5). Для этого необходимо в формулу (1) подставить выражение (5) и провести интегрирование по всем длинам волн (от нуля до бесконечности): (12).

Введем новую переменную:

(13).




Подставив (13) в (12), получим: (14).

Если учесть, что значение несобственного интеграла в (14) равно π⁴/15, получим:

(15).

Из сравнения (11) с (15) следует, что постоянная Стефана-Больцмана равна:

(16).

Оптическая пирометрия.

Оптической пирометрией называется совокупность методов измерения температуры тел, основанных на законах теплового излучения. Приборы, применяемые для этого, называются пирометрами.

Эти методы очень удобны для измерения температур различных объектов, где сложно или вообще невозможно применить традиционные контактные датчики. Это относится в первую очередь к измерению высоких температур.

В оптической пирометрии различают следующие температуры тела: радиационную, цветовую, яркостную.

Радиационная температура.

Радиационная температура Т_р тела- это температура абсолютно чёрного тела, при которой его энергетическая светимость R равна энергетической светимости R_m данного тела в широком диапазоне длин волн.

Если же измерить мощность, излучаемую некоторым телом с единицы поверхности в достаточно широком интервале волн и ее величину сопоставить с энергетической светимостью абсолютно черного тела, то можно, используя формулу (11), вычислить температуру этого тела, как

(17).

Определенная таким способом температура T_p будет достаточно точно соответствовать истинной температуре T при выполнении двух условий:

-оптическая система и детектор излучения должны иметь одинаковую чувствительность в широком диапазоне длин волн, соответствующем основной излучаемой мощности поверхности тела.

-коэффициент монохроматического поглощения поверхности тела должен быть близок к единице.

Для серого тела закон Стефана-Больцмана может быть записан в виде

R_m(T) = α_T σT⁴; где α_T< 1.

Подставляя данное выражение в формулу (17), получим

(18).

Из (18) следует, что для серого тела радиационная температура оказывается всегда ниже истинной (T_p< T).

Цветовая температура.

Спектральная плотность энергетической светимости серых тел (или тел близких к ним по свойствам) с точностью до постоянного коэффициента (коэффициента монохроматического поглощения) пропорциональна спектральной плотности энергетической светимости абсолютно черного тела. Следовательно, распределение энергии в спектре серого тела такое же, как и в спектре абсолютно черного тела при той же температуре.

Для определения температуры серого тела достаточно измерить мощность I(λ,Т), излучаемую единицей поверхности тела в достаточно узком спектральном интервале (пропорциональную r(λ,Т)), для двух различных волн. Отношение I(λ,Т) для двух длин волн равно отношению зависимостей f(λ,Т) для этих волн, вид которых дается формулой (5):

(19).

Из данного равенства можно математическим путем получить температуру Т. Полученная таким образом температура называется цветовой. Цветовая температура тела, определенная по формуле (19), будет соответствовать истинной, если коэффициент монохроматического поглощения не сильно зависит от длины волны. В противном случае понятие цветовой температуры теряет смысл. Цветовая температура серого тела совпадает с истинной температурой и может быть найдена также из закона смещения Вина.

Таким образом,

цветовая температураТ_ц тела- это температура абсолютно чёрного тела, при которой относительные распределения спектральной плотности энергетической светимости абсолютно чёрного тела и рассматриваемого тела максимально близки в видимой области спектра.

Обычно для определения цветовой температуры выбирают длины волн λ₁=655 нм (красный цвет), λ₂= 470 нм (зелено-голубой цвет).
Яркостная температура.

Яркостная температура Т_я тела – это температура абсолютно чёрного тела, при которой его спектральная плотность энергетической светимостиf(λ,T), для какой либо определённой длины волны, равна спектральной плотности, энергетической светимости r(λ,Т) данного тела для той же длины волны.

Так как для нечерного тела спектральная плотность энергетической светимости при определенной температуре будет всегда ниже чем у абсолютно черного тела, то истинная температура тела будет всегда выше яркостной.

В качестве яркостного пирометра широко используется пирометр с исчезающей нитью. Принцип определения температуры основан на визуальном сравнении яркости раскаленной нити лампы пирометра с яркостью изображения исследуемого объекта. Равенство яркостей, наблюдаемое через монохроматический светофильтр (обычно измерения проводят на длине волны λ=660 нм), определяется по исчезновению изображения нити пирометрической лампы на фоне изображения раскаленного объекта. Накал нити лампы пирометра регулируется реостатом, а температура нити определяется по градуировочному графику, или таблице. Если температура нити высока, то для ослабления потока излучения применяется также и нейтральный светофильтр.

Пусть мы в результате измерений получили равенство яркостей нити пирометра и исследуемого объекта и по графику определили температуру нити пирометра Т₁. Тогда, на основании формулы (3) можно записать:
f (λ,T₁) α₁(λ,T₁) = f (λ ,T₂) α₂( λ, T₂ ) (20),
где α₁(λ,T₁) и α₂(λ,T₂) коэффициенты монохроматического поглощения материала нити пирометра и исследуемого объекта соответственно. T₁ и T₂ – температуры нити пирометра и объекта. Как видно из (20), равенство температур объекта и нити пирометра будут наблюдаться только тогда, когда будут, равны их коэффициенты монохроматического поглощения в наблюдаемой области спектра α₁(λ,T₁)=α₂(λ,T₂). Если α₁(λ,T₁) > α₂(λ,T₂), мы получим заниженное значение температуры объекта, при обратном соотношении - завышенное значение температуры.


5. Поляризация света. Поляризованный свет. Плоскополяризованный свет, свет, поляризованный по кругу и эллипсу. Получение поляризованного света. Двойное лучепреломление в кристаллах. Призма Николя Поляризация света при отражении Угол Брюстера, закон Брюстера. Оптически активные среды Вращение плоскости поляризации.
Поляризованный свет. Плоскополяризованный свет, свет, поляризованный по кругу и эллипсу.

В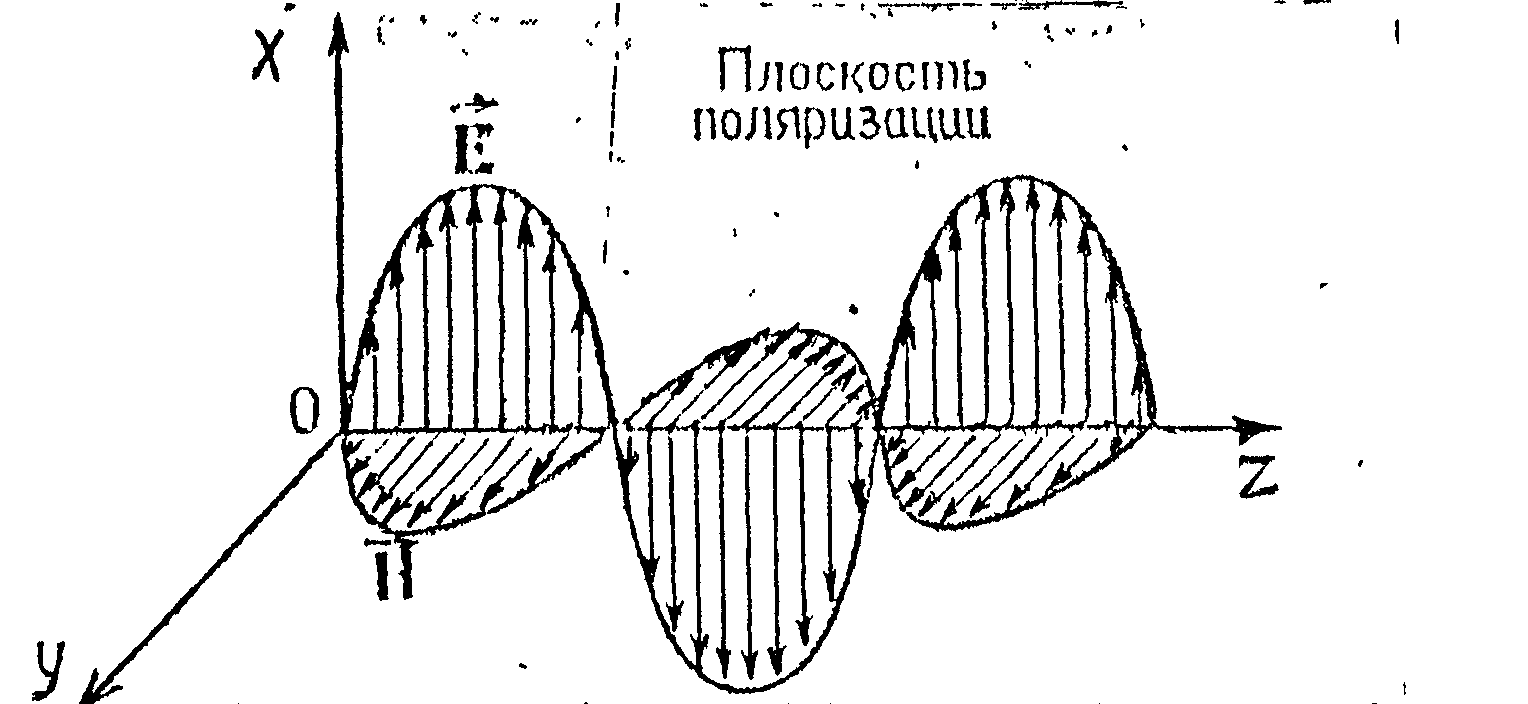
электромагнитной волне, распространяющейся в свободном пространстве, векторы напряженности электрического (Ē) и магнитного (Н) полей взаимно перпендикулярны, изменяются синхронно (см. рис.1) и их величины связаны соотношением:

(1)

где ε₀ и μ₀ ^- соответственно электрическая и магнитная постоянные.

Поэтому в световой электромагнитной волне достаточно знать поведение .лишь одного из векторов. Обычно для этой цели выбирают вектор Ē.

В естественном свете имеются колебания вектора Ē волны, совершающиеся в различных направлениях, перпендикулярных к лучу. Свет, в котором направления колебаний вектора Ē упорядочены каким либо образом, называется поляризованным.

Поляризация света - это физическая характеристика оптического излучения, описывающая неэквивалентность различных направлений колебаний вектора Ē волны в плоскости, перпендикулярной световому лучу.

Волна называется линейно поляризованной (или иначе плоско поляризованной), если в процессе распространения волны вектор Ē лежит в одной плоскости, параллельной направлению распространения волны.

Плоскостью поляризации называется плоскость, проходящая через направление колебаний электрического вектора Ē линейно поляризованной световой волны и направление распространения этой волны (плоскость PР1, см. рис.2а). Плоско поляризованную волну излучает, например, отдельный атом.

Волна называется поляризованной по кругу (или волной с циркулярной поляризацией), если конец вектора Ē описывает в плоскости, перпендикулярной направлению распространения волны, окружность.

При вращении конца вектора Ē по часовой стрелке говорят о правой круговой поляризации волны, а при вращении против часовой стрелки, соответственно, о левой круговой поляризации. Если конец вектора Ē описывает в пространстве эллипс, то тогда говорят о эллиптически поляризованной волне.
П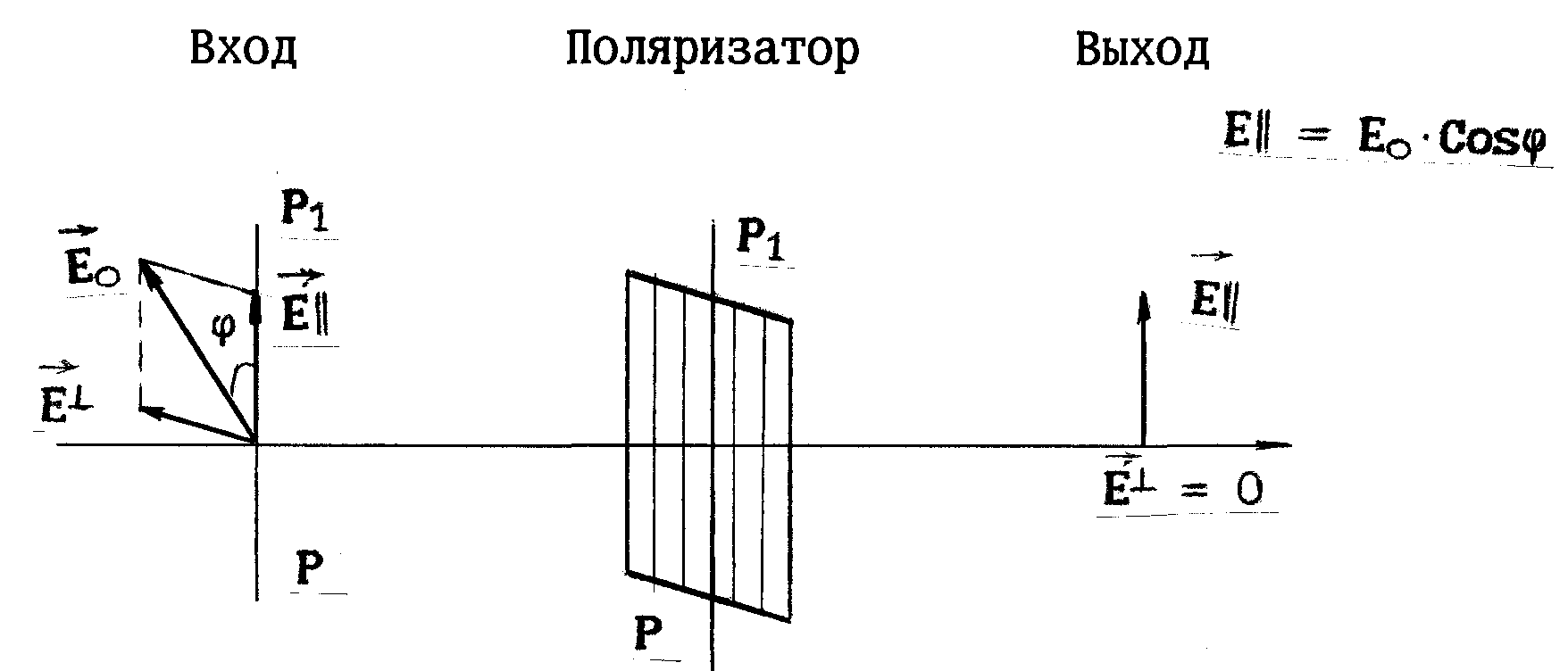
олучение поляризованного света. Прохождение света через поляризатор. Закон Малюса.
Для экспериментального анализа поляризации света используют поляризаторы. Поэтому кратко рассмотрим их принцип действия. Поляризатор представляет собой устройство для получения линейно поляризованного света. Действие поляризаторов основано на том, что они пропускают световые колебания лишь в определенной плоскости, которая проходит через ось поляризатора.
Рис.4. Прохождение линейно поляризованного света через поляризатор. РР' - ось поляризатора.
Линейно поляризованная волна, падающая на поляризатор, может быть разложена на две взаимно перпендикулярные составляющие: Е|| - параллельную оси поляризатора, и Е┴ - перпендикулярную этой оси (см. рис. 4).

Составляющая E┴, перпендикулярная плоскости РР', поглотиться поляризатором, а составляющая Е|| пройдет через поляризатор. .Поэтому амплитуда волны, прошедшей через поляризатор, будет равна Е = Ео·соsφ , (10) где φ - угол между направлением колебаний вектора напряженности электрического поля падающей на поляризатор волны и плоскостью поляризатора.

Интенсивность световой волны пропорциональна квадрату амплитуды напряженности, поэтому интенсивность света прошедшего через поляризатор будет равна: ι = ιo·cos²φ , (11)

где ιo - интенсивность, падающего на поляризатор линейно поляризованного света. Соотношение (11) носит название закона Малюса и формулируется следующим образом:

интенсивность света, прошедшего через поляризатор пропорциональна интенсивности линейно поляризованного света, падающего на поляризатор и квадрату косинуса угла между плоскостью поляризации падающего света и плоскостью поляризатора.

При падении на поляризатор естественного света, как следует из формулы (7), интенсивность любых двух взаимно перпендикулярных составляющих всегда будут равны друг другу. Т.е. при любом положении поляризатора ι║ = ι┴ (12)

Следовательно, интенсивность естественного света, прошедшего через поляризатор, всегда будет равна ι = ι₀/2, (13)

где ιo - интенсивность естественного света, падающего на поляризатор.
Фазовые пластинки Двойное лучепреломление.

При падении света на оптически анизотропную среду (оптические свойства которой в разных направлениях не одинаковы) в ней в общем случае, возникают две волны, распространяющиеся от границы раздела в различных направлениях и с различными скоростями. Это явление называется двойным лучепреломлением.

Гюйгенс объяснил это явление, предположив, что падающая на анизотропную среду волна порождает в кристалле вторичные волны двух видов: сферическую (обыкновенную) и эллиптическую (необыкновенную). Скорость необыкновенной волны, а, следовательно, и показатель преломления для необыкновенной волны зависит от направления распространения этой волны в кристалле.

Оказалось, что эти две волны линейно поляризованы во взаимно перпендикулярных плоскостях.

В анизотропных кристаллах всегда имеется одно или два направления, вдоль которого двойное лучепреломление отсутствует. Это направление называется оптической осью кристалла.

Рассмотрим распространение света через пластинку кристалла в направлении перпендикулярном оптической оси. Падающий нормально на такую пластинку пучок света будет распространяться в прежнем направлении, т.е. два линейно поляризованных луча (обыкновенный и необыкновенный), возникающих в кристалле, будут при этом идти не преломляясь, т.е. не изменяя своего направления, но с различной скоростью.

Обозначим n₀–показатель преломления волны, в которой вектор перпендикулярен оптической оси (обыкновенная волна), n_e - показатель преломления волны, в которой вектор лежит в плоскости, содержащей оптическую ось и направление распространения волны (необыкновенная волна) (см.рис.4).

Фазовые скорости V₀ V_e этих волн будут равны соответственно:

V₀ = С/nо И V_е = С/n_е, (12)

где С - скорость света в вакууме.

Пусть на пластинку кристалла падает линейно поляризованная волна, вектор которой образует некоторый угол α с оптической осью кристалла

( см.рис.4).

Составляющие Е₀ и Е_e, на которые можно разложить вектор , колеблются в одной фазе. После прохождения световой волны через пластинку между составляющими Е₀ и Е_e возникнет оптическая разность хода:

(13)

и, соответственно, разность фаз: (1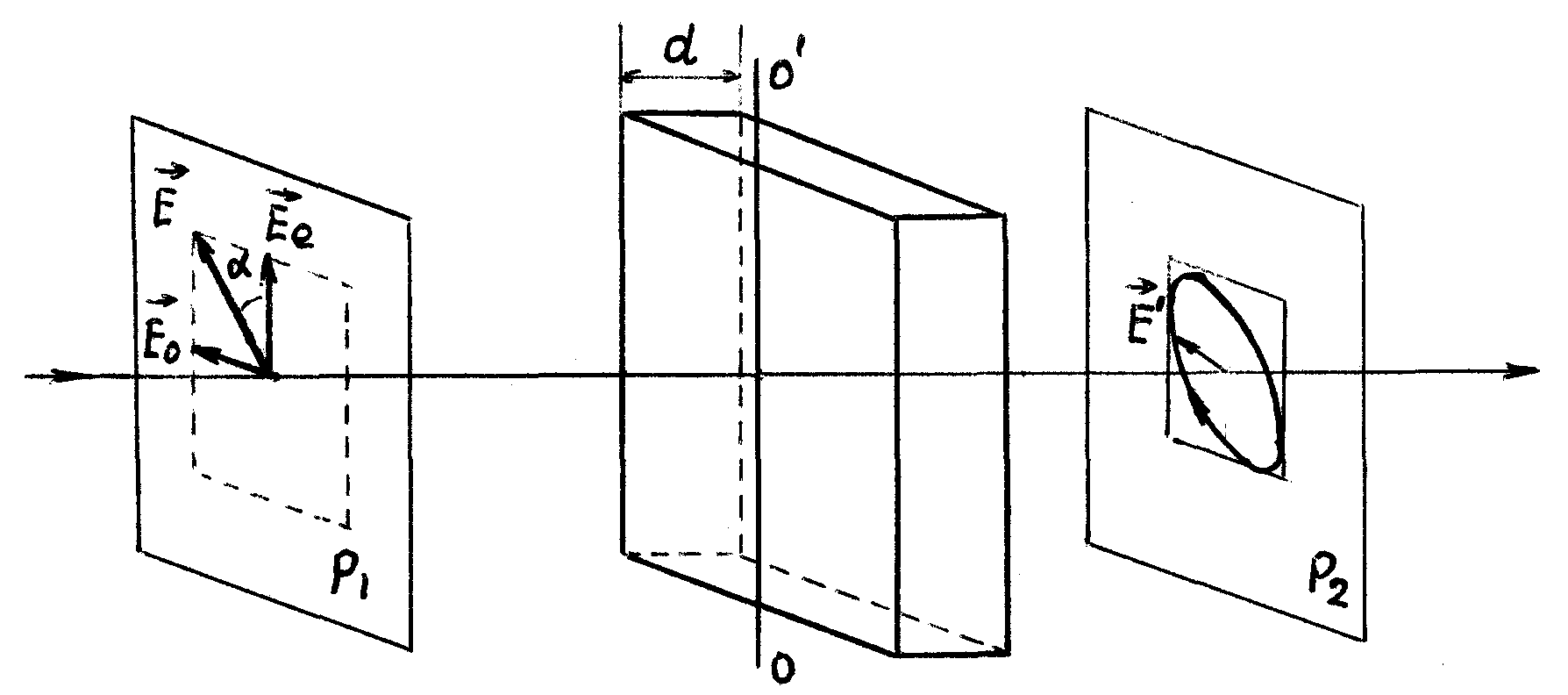4)

К
ристаллическая пластинка, которая вносит дополнительную разность фаз между двумя взаимно перпендикулярными составляющими падающей на нее световой волны, называется фазовой пластинкой. Поэтому, прошедшая пластинку волна, станет в общем случае эллиптически поляризованной (см. п. 2.1).
Рис.4. Прохождение линейно поляризованного света через пластинку анизотропного кристалла толщиной d . 00' - оптическая ось кристалла.

Чтобы с помощью фазовой пластинки можно было получить из линейно поляризованного света свет с круговой поляризацией, а значит и наоборот из круговой - линейно поляризованный, необходимо, чтобы угол между осью кристалла и направлением вектора был равен π/4, а разность фаз между взаимно перпендикулярными составляющими при прохождении пластинки равнялась

δ = (2m+1) •π/2, (15)

где m -целое число. Разность хода при этом будет равна

∆ = (2m+1) ·λ/4. (16)

Из формулы (13) видно, что при заданных по и пе это условие удовлетворяется подбором толщины пластинки d . В результате при

(17)

получается, так называемая, пластинка в четверть длины волны (пластинка λ/4).
Призмы Николя (Поляризационные приборы и использование поляризованных лучей).

Д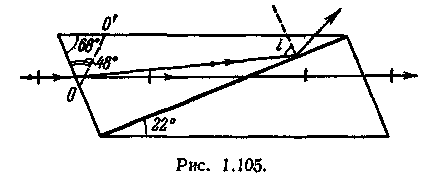ля изготовления поляризаторов и анализаторов на практике применяют двоякопреломляющи е кристаллы. Из монокристаллов исландского шпата изготовляют так называемые призмы - Николя (или просто — николи). Николь представляет собой двойную призму, склеенную в промежутке канадским бальзамом. Призмы выкалываются из кристалла под такими углами, чтобы необыкновенный луч, падающий на переднюю грань, проходил насквозь, практически не преломляясь (рис. 1.105). Обыкновен­ный луч при этом преломляется и падает на прослойку канадского
бальзама под большим углом I. Показатель преломления клея n_б меньше показателя преломления обыкновенного луча n_o,так что sin i> n_б/n_o; этот луч испытывает полное внутреннее отра­жение и выходит через боковую грань призмы, где затем полностью поглощается.
Отражение света на границе двух прозрачных сред. Формулы Френеля.Угол Брюстера.
Когда свет достигает границы двух прозрачных сред с разными оптическими свойствами, он частично проходит во вторую среду, изменяя направление в случае наклонного падения (преломляется), и частично возвращается в первую среду (отражается).

Направление отраженного и преломленного лучей света хорошо описывается законами геометрической оптики. Однако эти законы ничего не говорят о поляризации и интенсивности отраженного и преломленного света.

Физические причины появления преломленной и отраженной световых волн на границе раздела те же, что и причины, приводящие к изменению фазовой скорости волн при распространении их в среде по сравнению со скоростью света в вакууме (см. лаб. работу N1"Дисперсия света").

Электрическое поле падающей волны раскачивает, входящие в состав вещества среды заряженные частицы, которые при этом становятся источниками вторичных волн. Отраженная и преломленная волны представляют собой результат сложения падающей и когерентных с ней вторичных волн.

Введем термин коэффициент отражения (R) границы раздела двух сред, как отношение интенсивности света (т.е. среднего по времени потока энергии электромагнитной волны) отраженного от поверхности к интенсивности падающего света:

R = I_отр/I_пад (18)

Для нормального падения света коэффициент отражения не зависит от поляризации волны и выражается через показатели преломления граничащих сред: (19)

Значение R не изменится, если n₁ и n₂ поменять местами, поэтому коэффициент отражения на границе прозрачных сред не зависит от того, в каком направлении падает свет, из первой среды во вторую или наоборот

Коэффициент отражения тем меньше, чем ближе показатели преломления граничащих сред. Для границы стекла (n₁=1,5) и воздуха (n₂= 1) R=4%. При n₁= n₂ отражение вообще отсутствует.

К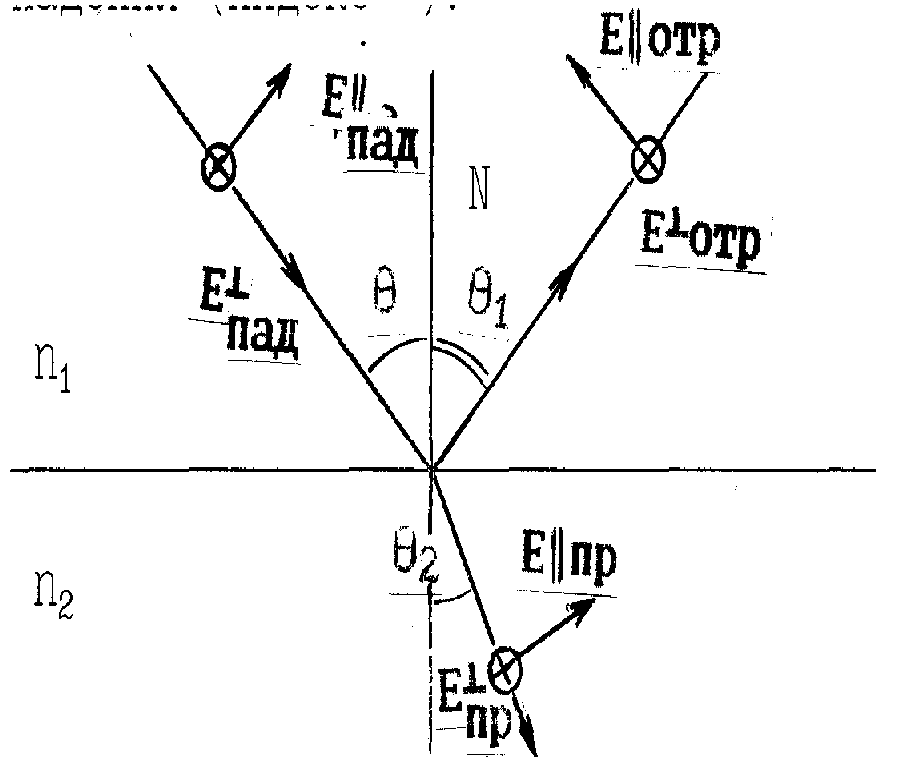
оэффициент отражения при наклонном падении луча зависит от поляризации падающего света. Поэтому разложим каждую из трех волн - падающую, отраженную и преломленную на две составляющие: поляризованную в плоскости падения, т.е. в плоскости, в которой лежит падающий луч и нормаль N, восстановленная из точки падения (снабдим эти составляющие индексом || ), и поляризованную в плоскости перпендикулярной плоскости паления ( индекс ┴ ).
Рис.5. Направления векторов Е_║ и Е┴ в падающей, отраженной и преломленной волнах

Френелем получены формулы для коэффициентов отражения составляющих световой волны параллельной и перпендикулярной плоскости падения луча, выраженные через угол падения θ и угол преломления θ₂ луча.

(20)

Коэффициент отражения естественного света можно получить, если

рассматривать его как сумму двух некогерентных волн одинаковой интенсивности:

I_ест= I₌+I_┴=I_ест/2+I_уст/2 (21)

Поэтому коэффициент отражения естественного света будет равен:

Rеcт =(R┴ + R_║ )/2. (22)

Из графиков на рис.6а видно, что при некотором угле падения R_║ = 0. Это следует и из формулы (20). При θ + θ₂ = π/2 получим, что знаменатель равен бесконечности и выражение (20) для R_║ обращается в нуль.

Так как по закону преломления

sin θ /sin θ₂ = n₂/n₁, (23) то при θ₂ = π/2 - θ получим:

sin θ /sin(π/2 - θ) = sin θ /cos θ = tg θ = n₂/n₁. (24)

Следовательно, при падении света под углом θ, определяемым .выражением:

Tgθ_б = n₂/n₁ (25)

составляющая, имеющая поляризацию параллельную плоскости падения, проходит во вторую среду полностью, не отражаясь (см.рис.6б), а составляющая. поляризованная перпендикулярно плоскости падения частично отражается.

Поэтому при падении на границу раздела естественного света под углом, определяемым выражением (25), отраженный свет будет линейно поляризован в плоскости, перпендикулярной плоскости падения, а преломленный - частично поляризованным.

Зависимость угла, при котором наблюдается линейная поляризация отраженной волны, от отношения показателей преломления двух сред (25) называется законом Брюстера, а соответствующий угол θ_Б - углом Брюстера.
Оптически активные вещества.

Оптически активными называются вещества, после прохождения через которые плоскость поляризации линейно поляризованного света поворачивается на некоторый угол (φ) (Рис.5).

Для определенной длины волны угол поворота плоскости РР' прямо пропорционален толщине слоя вещества ι , пройденного светом:
φ
= α·ι (град) (14)

Рис.5. Поворот плоскости поляризации в оптически активном веществе.
где α - коэффициент пропорциональности, называемый постоянной вращения.

Постоянная вращения зависит от природы вещества, температуры и длины волны света. Зависимость постоянной вращения от длины волны называется вращательной дисперсией. В растворах постоянная вращения прямо пропорциональна концентрации (С) оптически активного вещества, поэтому

φ = [α]·С·ι (град) (15)
где [α] - удельная постоянная вращения вещества, (град-см²/г) Соотношение (15) выражает закон Био.

Оптически активные вещества существуют в двух модификациях - пра-вовращающей и левовращающей. Если смотреть навстречу, то в правовраща-ющих веществах плоскость поляризации поворачивается вправо (по часовой стрелке). Постоянные вращения для правовращающей и левовращающей модификации одного и того же вещества одинаковы.
Теория вращения плоскости поляризации.

Френель показал, что вращение плоскости поляризации линейно поляризованного света можно объяснить, если допустить, что в оптически активной среде монохроматические волны правой и левой круговой поляризации имеют различные фазовые скорости и, следовательно, различные показатели преломления, т.к. фазовая скорость (v) связана с показателем преломления (n) выражением:
V = С/n (16) где С - скорость света в вакууме.

Рассмотрим линейно поляризованную волну как суперпозицию двух векторов Еп и Ел , которые с течением времени вращаются с одинаковой частотой вправо и влево. (Рис. ба). Пусть в заданный момент времени

t = const, результирующий вектор Ер(о) = Еп₍₀₎ + Ел₍₀₎ в точке пространства z = 0 был направлен вдоль оси OY (см. рис.6 ). На расстоянии z = d вектора Еп₍₀₎ и Ел₍₀₎ повернутся по отношению к их положению в точке Z = 0 соответственно на углы:
_δ1=ω·d/Vп;δ₂=ω·d/Vл . (17)

где Vп , Vл - скорости волн, поляризованных по правому и левому кругу соответственно, d/Vп, d/Vл - время распространения этих волн на расстояние d. Следовательно, из-за разности скоростей Vп и Vл, между векторами Еп₍₀₎ и Ел ₍₀₎ в точке z = d возникает разность фаз. Ь δ=δ₁-δ₂=ω·d·(1/Vп–1/Vл) (18)
Результирующий вектор E^’p₍₀₎ , как видно из рис.6, при этом повернется

на угол δ/2, т.е. при прохождении волной расстояния d плоскость поляризации повернется на угол φ=δ/2=ω·d/2·(1/V_п-1/V_л) (19)

Используя соотношения:

ω = 2·С/λ; V_п=C/n_п; V_л = С/n_л (20)

где λ - длина волны в вакууме, n_п и n_л соответствующие показатели преломления, формулу (20) можно переписать в виде: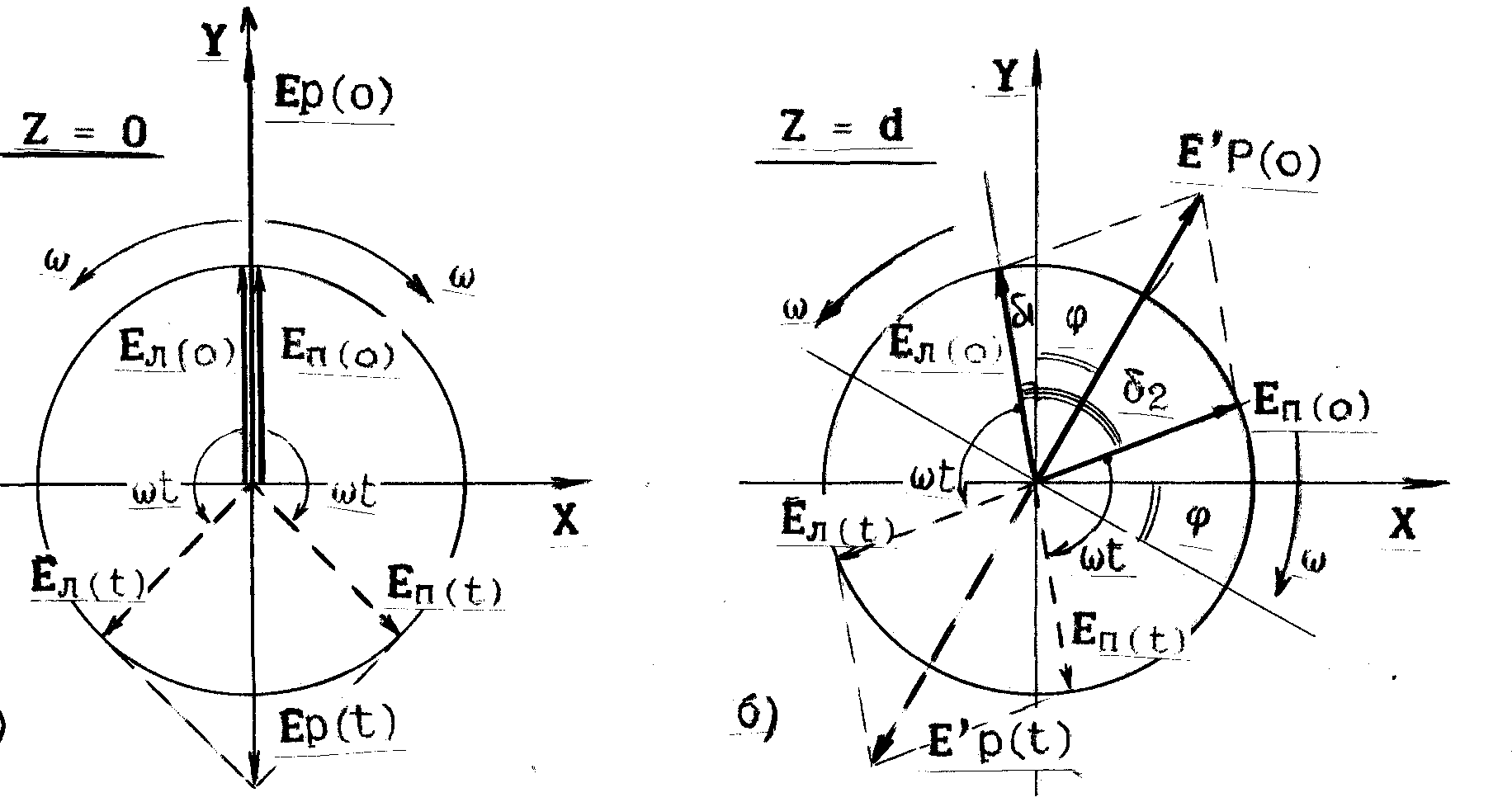


(21) таким образом получим: (22)

Рис.6. Сложение волн поляризованных по правому и левому кругу : а) на входе в оптически активное вещество, б) после прохождения в оптически активном веществе пути равного d.

Причины различия скоростей волн, поляризованных по правому и левому кругу, в оптически активных веществах связаны с асимметричным строением молекул. Такие молекулы не обладают зеркальной симметрией. При зеркальном отражении молекул "правой" модификации получаются молекулы "левой" модификации.

Например молекулы сахара могут быть представлены в виде правой и левой спирали. Эти две модификации обладают одинаковой химической формулой, но поворачивают плоскость поляризации света в различных направлениях

Вращение плоскости поляризации в магнитном поле.

Оптически неактивные вещества под действием магнитного поля становятся активными. Это явление вращения плоскости поляризации в магнитном поле называется эффектом Фарадея.

При распространении света вдоль силовых линий магнитного поля угол поворота плоскости поляризации пропорционален пути (L), проходимому светом в веществе, и индукции магнитного поля (В):

 = RB (23)

где R - постоянная Верде, зависящая от типа вещества и длины волны распространяющегося света.

Направление вращения в одном и том же веществе не зависит от направления распространения света (по полю или против поля), а определяется лишь направлением магнитного поля, т.е. вектора В. Если вращение плоскости поляризации происходит вправо (при наблюдении вдоль вектора В), то вещества называются положительными.

Явление магнитного вращения плоскости поляризации связано с эффектом Зеемана, т.е. с расщеплением линий

6. Дисперсия свет., Явление дисперсии. Опыты Ньютона. Нормальная и аномальная дисперсии. Электронная теория дисперсии
Закон преломления света. Явление дисперсии. Нормальная и аномальная дисперсии.

Э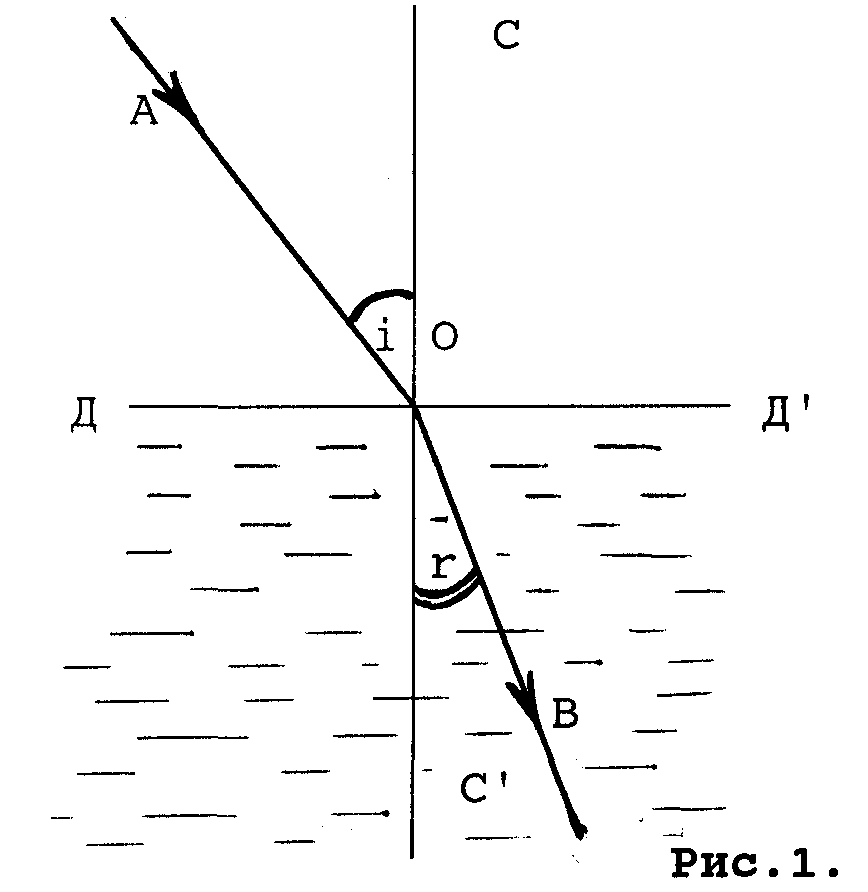кспериментальные исследования показывают, что при прохождении границы раздела двух сред луч света испытывает преломление (рис.1). Это явление подчиняется следующим закономерностям:

Преломление светаД Д' - граница раздела двух сред,

АО и OB - падающий и преломлённый лучи, соответственно,

СС′- перпендикуляр (нормаль) к поверхности раздела, восстановленный в точке падения О,

i и г - углы падения и преломления луча соответственно.

1. 
   преломлённый луч лежит в одной плоскости с падающим лучом и нормалью к поверхности раздела в точке падения;
   
2. 
   отношение синусов падения и преломления лучей света с фик­сированной длиной волны есть величина постоянная для двух данных веществ: Sin i / Sin r = n₂₁
   

Постоянную n₂₁ называют коэффициентом (показателем) преломления второй среды относительно первой. Показатель преломления какой либо среды относительно вакуума обозначают n и называют показателем преломления данной среды (вещества). Таким образом, если луч падает из вакуума на вещество, то закон преломления записывается в виде:

Sin i / Sin r = n (1)

Было обнаружено, что значение показателя преломления зависит от длины волны (или частоты ν = C/ λ, где C - скорость света в вакууме) падающего света. Эта зависимость оказывается различной для разных веществ, что учитывают введением понятия о дисперсии (Д) вещества, которая характеризует скорость изменения n в зависимости от λ:

Д = dn / dλ. (2)

О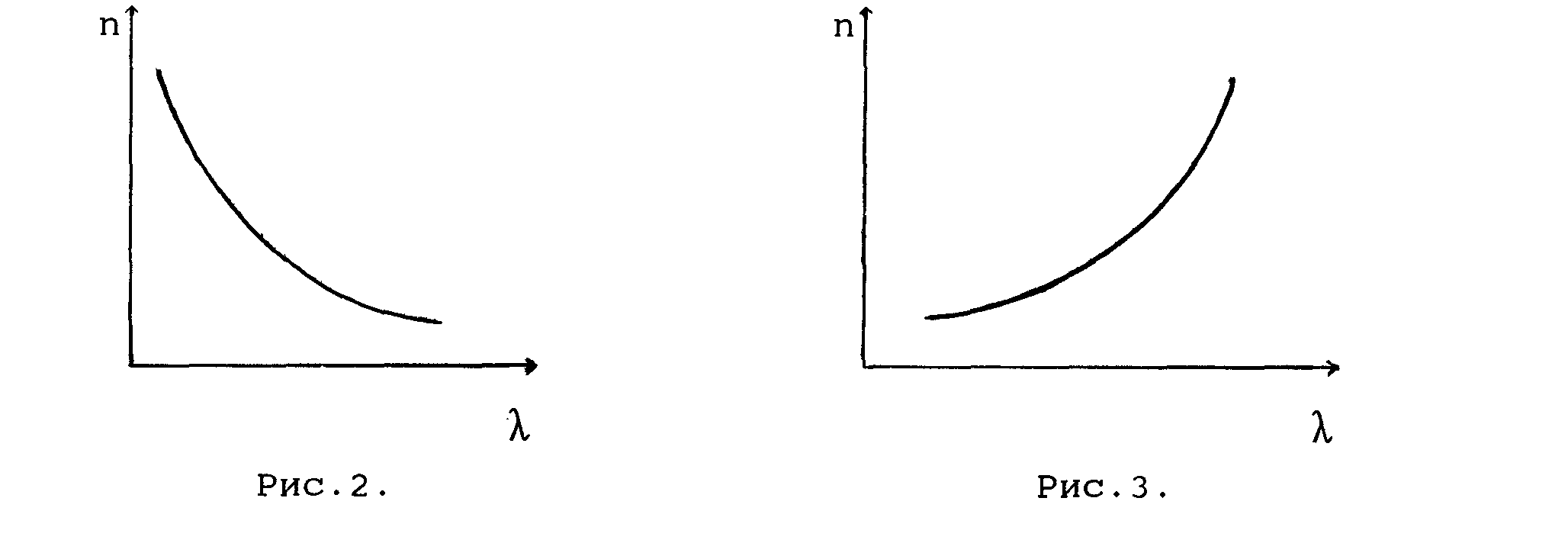бычно для диспергирующих (Д< 0) сред в области слабого поглощения (прозрачности) значения n уменьшаются с ростом длины волны (рис.2).Этой зависимости, называемой нормальным законом дисперсии (нормальной дисперсией), соответствует Д > 0 . Однако в области сильного поглощения обнаруживается обратный ход зависимости n от λ (рис.3). Это явление называют аномальной дисперсией и ему соответствует Д >0 .

Изложенные экспериментальные факты объясняются в рамках электромагнитной теории света и электронной теории вещества.

Элементарная теория дисперсии света. Электронная теория дисперсии

Максвелл показал, что свет представляет собой электромагнитную волну. Фазовые скорости распространения такой волны в веществе (V) и в вакууме (C) различны. Соотношение между ними определяется значениями диэлектрической (ε) и магнитной (μ) проницаемостей вещества: C/ V =

Для немагнитных сред можно принять μ = 1. ТогдаC / V = (3)

то есть фазовая скорость света в веществе в раз меньше, чем в вакууме. Это позволяет объяснить явление преломления света следующим образом:

Пусть в момент времени t = 0 некоторая точка А, принадлежащая фронту плоской монохроматической волны, падающей под углом i, достигает границы раздела вакуум - оптическая среда (рис.4). За время Δt свет пройдёт в среде путь АД = V·∆t. За это же время свет от некоторой точки В фронта волны пройдёт путь ВС = V·∆t, достигнув границы раздела. Поскольку C > V, то BC > AC, и фронт CD волны в среде должен повернуться так, чтобы направление его распространения в среде относительно нормали составляла некоторый новый угол r < i.. Учитывая равенство углов со взаимно перпендикулярными сторонами (см. рис.4), видим, что

ВС = AC Sin i, АД = AC Sin r тогда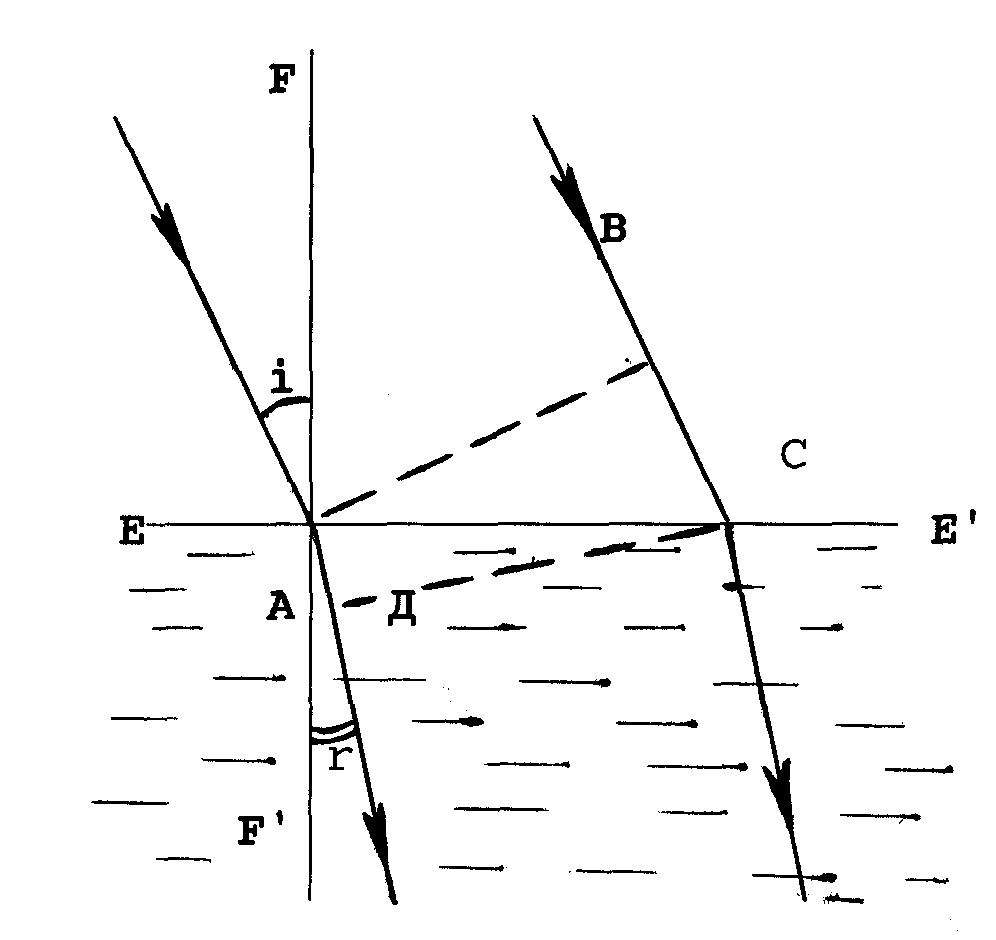

== то есть

С / V = Sin i / Sin r (4)

Сравнивая выражения (1), (3) и (4) найдём, что C/ V = n = (5)