Высшая математика. Шп вышмат. Уравнение, которое описывает зависимость координат каждой точки прямой
 Скачать 35.08 Kb.
|
|
1️⃣Уравнение, которое описывает зависимость координат каждой точки прямой в декартовой системе Oxy O x y , называется уравнением прямой на плоскости. Фактически, уравнение прямой на плоскости – это уравнение с двумя переменными, которые обозначаются как x и y . —Во-первых, две прямые на плоскости могут совпадать. Это возможно в том случае, когда прямые имеют по крайней мере две общие точки. —Во-вторых, две прямые на плоскости могут пересекаться. В этом случае прямые имеют одну общую точку, которую называют точкой пересечения прямых. —В-третьих, две прямые на плоскости могут быть параллельными. ОПРЕДЕЛЕНИЕ. Углом между прямой l и плоскостью λ называется угол φ между прямой l и ее проекцией на плоскость λ . Из определения следует, что угол между прямой и плоскостью всегда острый. 2️⃣Уравнение прямой на плоскости в прямоугольной системе координат Oxy - это линейное уравнение с переменными x и y, которому отвечают координаты всех точек прямой и не удовлетворяют координаты никаких прочих точек
Во-первых, две прямые могут совпадать, то есть, иметь бесконечно много общих точек (по крайней мере две общие точки). Во-вторых, две прямые в пространстве могут пересекаться, то есть, иметь одну общую точку. В этом случае эти две прямые лежат в некоторой плоскости трехмерного пространства. В-третьих, две прямые в пространстве могут быть параллельными. В этом случае они лежат в одной плоскости и не имеют общих точек. В геометрии за угол между двумя прямыми принимается МЕНЬШИЙ угол, из чего автоматически следует, что он не может быть тупым.Если прямые перпендикулярны, то за угол между ними можно принимать любой из 4 углов. 3️⃣Производная функции – отношение приращения функции к приращению аргумента при бесконечно малом приращении аргумента: 𝑓′(𝑥)=Δ𝑓/Δ𝑥 при Δ𝑥→0 Дифференциальное исчисление – это раздел анализа математического, связанный главным образом с понятиями производной и дифференциала функции. В дифференциальном исчислении изучаются правила вычисления производных (законы дифференцирования) и применения производных к исследованию свойств функций. 5️⃣Определенный интеграл от функции f(x)в пределах от a до b вводится как предел суммы бесконечно большого числа слагаемых, каждое из которых стремится к нулю Основные свойства определенного интеграла 1.Значение определенного интеграла не зависит от обозначения переменной интегрирования:  2. Постоянный множитель можно выносить за знак определенного интеграла: 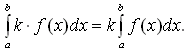 3. Определенный интеграл от алгебраической суммы двух функций равен алгебраической сумме определенных интегралов от этих функций:  4.Если функция y = f(x) интегрируема на [a, b] и a < b < c, то  5. (теорема о среднем). Если функция y = f(x) непрерывна на отрезке [a, b], то на этом отрезке существует точка 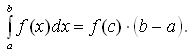 , такая, что 6️⃣ https://math.semestr.ru/transp/model.php найти переменные задачи X=(xij), i=1,2,...,m; j=1,2,...,n, удовлетворяющие системе ограничений (цифра 2 на математической модели) , условиям неотрицательности и обеспечивающие минимум целевой функции 7️⃣В клетку (1,1) занесем меньшее из чисел  , то есть  . Если  , то  и первый потребитель  будет полностью удовлетворен. В дальнейшем 1-й столбец таблицы в расчет не принимается: в нем переменные  для  .Двигаясь вправо по первой строке таблицы, заносим в соседнюю клетку (1,2) меньшее из чисел  и  , то есть  . Если  , то запасы первого поставщика исчерпаны и первая строка таблицы в дальнейшем в расчет не принимается. Переходим к аналогичному распределению запаса груза второго поставщика.Если  , то  . При этом запас первого поставщика будет исчерпан, а потому  для  . Первая строка из дальнейшего рассмотрения исключается. Переходим к распределению запасов второго поставщика. В клетку (2,1) заносим наименьшее из чисел  .Заполнив таким образом клетку (1,2) или (2,1), переходим к загрузке следующей клетки по второй строке либо по второму столбцу. Процесс распределения по второй, третьей и последующим строкам (столбцам) производится аналогично распределению по первой строке или по первому столбцу до тех пор, пока не исчерпаются ресурсы. Последней заполняется клетка  .8️⃣Каноническая форма ЗЛП - задача линейного программирования вида ax = b, где a - матрица коэффициентов, b - вектор ограничений. 9️⃣ (графический) способ решения задач линейного программирования обычно используется для решения задач с двумя переменными, когда ограничения выражены неравенствами, а также задач, которые могут быть сведены к таким задачам. 1. Сформулировать ЗЛП. 2. Построить на плоскости {х1, х2} прямые, уравнения которых получаются в результате замены в ограничениях знаков неравенств на знаки точных равенств. 3. Найти полуплоскости, определяемые каждым из ограничений задачи. 4. Найти область допустимых решений. 5. Построить прямую c1x1 + c2x2 = h, где h - любое положительное число, желательно такое, чтобы проведенная прямая проходила через многоугольник решений. 6. Перемещать найденную прямую параллельно самой себе в направлении увеличения (при поиске максимума) или уменьшения (при поиске минимума) целевой функции. В результате, либо отыщется точка, в которой целевая функция принимает максимальное (минимальное) значение, либо будет установлена неограниченность функции на множестве решений. 7. Определить координаты точки максимума (минимума) функции и вычислить значение функции в этой точке. 🔟Общий смысл задач этого класса сводится к следующему. Предприятие выпускает n различных изделий. Для их производства требуется m различных видов ресурсов (сырья, материалов, рабочего времени и т.п.). Ресурсы ограничены, их запасы в планируемый период составляют, соответственно, b1, b2,..., bm условных единиц. Известны также технологические коэффициенты aij, которые показывают, сколько единиц i-го ресурса требуется для производства единицы изделия j-го вида ( ). Прибыль, получаемая предприятием при реализации изделия j-го вида, равна cj. В планируемом периоде значения величин aij, bi и cj остаются постоянными. Требуется составить такой план выпуска продукции, при реализации которого прибыль преприятия была бы наибольшей. 1️⃣1️⃣Линейное программирование — математический метод отыскания максимума или минимума линейной функции при наличии ограничений виде линейных неравенств или уравнений.Общая задача линейного программирования – это задача, в которой требуется найти максимум или минимум (оптимум) функции, называемой функцией цели, при ограничениях, заданных системой линейных неравенств или уравнений. 1️⃣2️⃣ Симплекс-метод является универсальным методом решения задач линейного программирования с любым числом переменных и с любым числом ограничений.В каждом из равенств присутствует одна определенная базисная переменная, взятая с единичным коэффициентом, а в других равенствах ее нет |
;