математика. Контрольная Математика. Выполнить деление комплексных чисел
 Скачать 34.06 Kb. Скачать 34.06 Kb.
|
ВЫПОЛНЕНИЕ ПРАКТИЧЕСКИХ ЗАДАНИЙ ПО ДИСЦИПЛИНЕ МАТЕМАТИКА Группа 21М571в Студент С.И. Сидоров МОСКВА 2022 Выполнить деление комплексных чисел 1.1 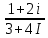 = =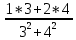 + +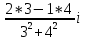 = =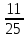 + +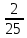 i=0,44+0,08i i=0,44+0,08i1.2 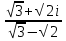 = =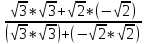 = =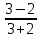 +i +i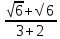 = =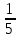 + +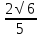 i=0,2+0,98i i=0,2+0,98i2. Вычислить пределы последовательностей 2.1 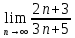 = =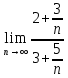 = =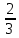 2.2 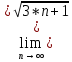 - - 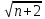 )= )=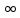 Домножим и разделим на 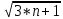 - - 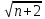 ) )= 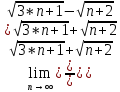 = = 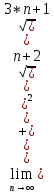 )= )=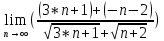 = =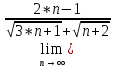 )=разделим числитель и знаменатель на sgrt(n) )=разделим числитель и знаменатель на sgrt(n)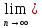 ( (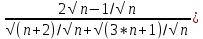 = =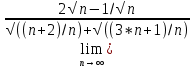 )= )=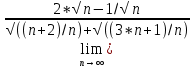 )= )=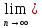 ( (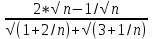 )= /сделаем замену a= )= /сделаем замену a=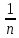 / / 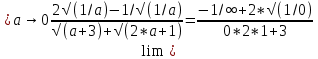 )= )= 3. Используя признаки Даламбера и Коши исследовать сходимость рядов 3.1 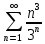 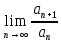 = =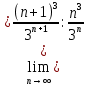 )= )=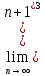 = =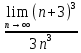 = = 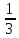 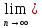 ( (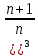 = = 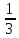 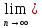 (1+ (1+ 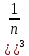 = = 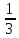 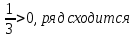 3.2 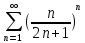 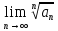 = =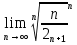 = =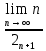 = =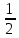 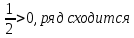 4. Найти производные сложных функций 4.1 Y= 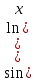 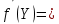 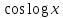 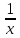 4.2 y= 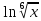 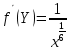 * *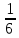 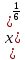 -1) = -1) =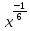 * * 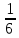 * *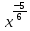 = = 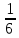 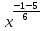 = =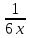 5. Вычислить неопределенный интеграл 5.1 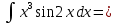 /Интеграл от произведения функции на константу есть эта константа на интеграл от данной функции:/ /Интеграл от произведения функции на константу есть эта константа на интеграл от данной функции:/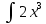 sin(x) cos(x) dx=2 sin(x) cos(x) dx=2 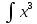 sin(x) cos(x)dx /интегрируем по частям sin(x) cos(x)dx /интегрируем по частям 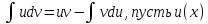 = = 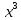 и dv(x)=3 и dv(x)=3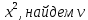 (x): (x):Интеграл от произведения функции на константу есть эта константа на интеграл от данной функции 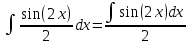 , пусть U=2x, тогда du=2dx ,подставим , пусть U=2x, тогда du=2dx ,подставим 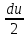 : :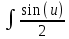 du Интеграл от произведения функции на константу есть эта константа на интеграл от данной функции: du Интеграл от произведения функции на константу есть эта константа на интеграл от данной функции: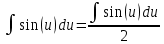 Интеграл от синуса – минус косинус: 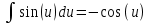 , результат - , результат -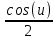 , если заменить u в , если заменить u в 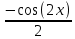 , получим , получим 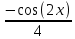 Интегрируем по частям: 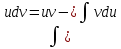 , пусть u(x)=- , пусть u(x)=- 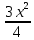 , dv(x)= - , dv(x)= - 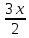 Пусть U=2x, тогда du=2dx, подставим 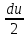 : : 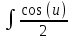 du duИнтеграл от произведения функции на константу есть эта константа на интеграл от данной функции: 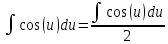 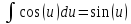 , результат , результат 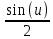 , заменим u в , заменим u в 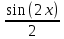 Интегрируем по частям: 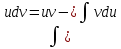 , пусть u(x)= - , пусть u(x)= - 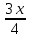 и пусть dv(x)=sin(2x) и пусть dv(x)=sin(2x)Затем du(x)=- 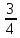 Пусть u=2x, тогда пусть du=2dx и подставим 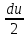 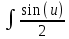 du duИнтеграл от произведения функции на константу есть эта константа на интеграл от данной функции: 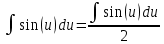 Интеграл от синуса есть минус косинус: 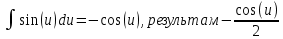 , если заменить u в , если заменить u в 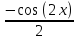 , учитывая что Интеграл от произведения функции на константу есть эта константа на интеграл от данной функции: , учитывая что Интеграл от произведения функции на константу есть эта константа на интеграл от данной функции: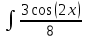 dx= dx= 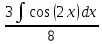 , пусть u=2x, тогда du=2dx, подставим , пусть u=2x, тогда du=2dx, подставим 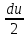 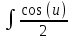 du Интеграл от произведения функции на константу есть эта константа на интеграл от данной функции: du Интеграл от произведения функции на константу есть эта константа на интеграл от данной функции: 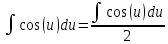 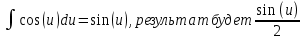 , если u заменить , если u заменить 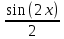 , получится , получится 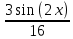 Результат будет: - 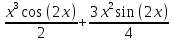 + + 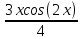 - - 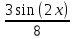 , добавляем постоянную интегрирования: , добавляем постоянную интегрирования:- 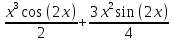 + + 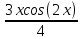 - - 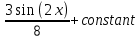 5.2 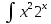 dx=- dx=- 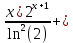 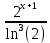 + + 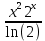 +C +C/ Интегрируем по частям: : 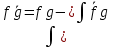 f= 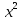 , g= , g=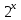 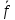 =2x, =2x, 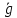 = =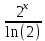 / /= 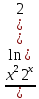 - - 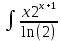 dx dx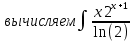 = / применяем линейность/= = / применяем линейность/= 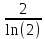 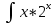 dx, вычисляем: dx, вычисляем: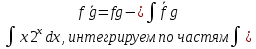 f=x, 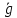 = =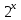 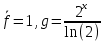 = 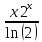 - - 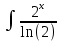 dx, вычисляем dx, вычисляем 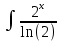 dx= dx= 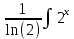 dx dxВычисляем 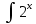 dx / dx / 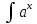 dx = dx =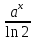 , при a=2 / = , при a=2 / =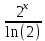 Подставляем вычисленные интегралы: 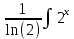 dx= dx= 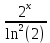 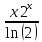 - - 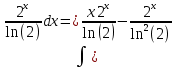 = = 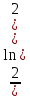 dx= dx=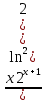 - - 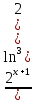 Подставим вычисленные интегралы: 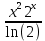 - - 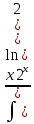 dx = dx = 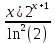 + + 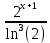 + +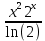 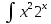 dx= - dx= - 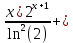 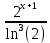 + + 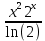 +C +C 6. Найти частные производные первого и второго порядка 6.1 z= 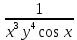 При нахождении 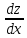 считаем аргумент y постоянным: считаем аргумент y постоянным: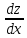 = - = - 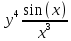 - 3 - 3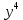 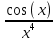 При нахождении 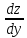 считаем аргумент x постоянным:+ считаем аргумент x постоянным:+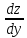 =4 =4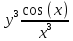 Находим вторые частные производные: 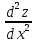 =(- =(-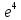 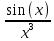 – 3 – 3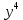 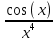 )` x = - )` x = - 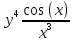 + 6 + 6 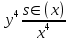 + 12 + 12 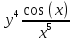 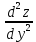 = (4 = (4 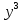 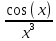 )`y= )`y=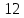  6.2 Z= 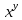 Находим частные производные: При нахождении 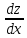 считаем аргумент y постоянным: считаем аргумент y постоянным: 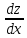 = =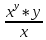 При нахождении 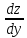 считаем аргумент x постоянным: считаем аргумент x постоянным: 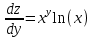 Находим вторые частные производные: 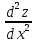 =( =(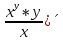 x = x =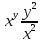 - - 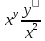 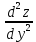 = ( = (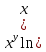 )) ´y = )) ´y = 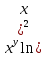 7. Найти сумму матриц 7.1 A= 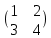 B= B=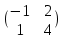 A+B= A+B=  )= )= 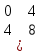 ) )7.2 A= ( 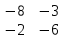 ) B= ( ) B= (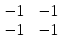 ) A+B = ( ) A+B = (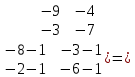 ) )8. Найти произведение матриц 8.1 A= 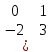 ) B= ( ) B= (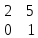 ) C=A*B= ) C=A*B= 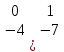 ) )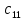 =0*2+1*0=0 =0*2+1*0=0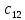 =0*5+1*1=1 =0*5+1*1=1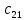 = (-2) *2+3*0=-4 = (-2) *2+3*0=-4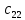 = (-2) *5+3*1=-7 = (-2) *5+3*1=-78.2 A= ( 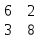 ) B= ( ) B= (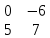 ) C=A*B= ( ) C=A*B= (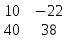 ) ) 6*0+2*5=10 6*0+2*5=10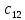 =6*(-6) +2*7=-22 =6*(-6) +2*7=-22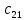 =3*0+8*5=40 =3*0+8*5=40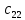 =3*(-6) +8*7=38 =3*(-6) +8*7=389. Найти определители матриц 9.1 A= ( 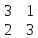 ) ) derA= 3*3-2*1=7 9.2 A= ( 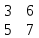 ) )derA= 3*7-5*6=-9 10.Решить систему уравнений 10.1 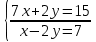 Сложение уравнений 8x=22 X=2.75 Подставим найденное значение х=2.75 2y=2.75-7 2y=-4.25 Y=-2.125 Ответ: X=2.75, Y=-2.125 10.2 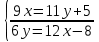 преобразуем преобразуем 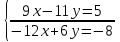 умножим первое уравнение на 4, а второе на 3 умножим первое уравнение на 4, а второе на 3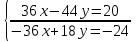 выполним сложение уравнений выполним сложение уравнений-26y=-4 Y= 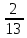 , подставим полученное значение y в первое уравнение , подставим полученное значение y в первое уравнение9*x=11* 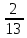 +5 +59*x= 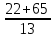 9*x= 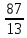 X= 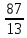 :9 :9X= 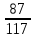 X= 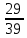 Ответ: X= 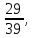 Y= Y=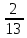 11.Для заданных векторов найти смешанное произведение 11.1 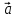 =(1;-2;1) =(1;-2;1) 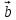 = (2;1;-2) = (2;1;-2) 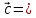 (1;1;1) (1;1;1)[ 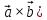 * *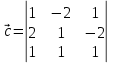 =1*1*1+(-2)*(-2)*1+1*2*1+1*1*1-(-2)*2*1-1*(-2)*1=1+4+2-1+4+2=12 =1*1*1+(-2)*(-2)*1+1*2*1+1*1*1-(-2)*2*1-1*(-2)*1=1+4+2-1+4+2=1211.2 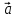 =(1;1;2) =(1;1;2) 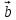 = (1;-1;3) = (1;-1;3) 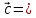 (-2;-2;2) (-2;-2;2)[ 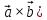 * *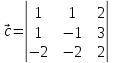 =1*(-1)*2+1*3*(-2)+2*1*(-2)-2*(-1)*(-2)-1*1*2-1*3*(-2)= -2-6-4-4-2+6=-12 =1*(-1)*2+1*3*(-2)+2*1*(-2)-2*(-1)*(-2)-1*1*2-1*3*(-2)= -2-6-4-4-2+6=-12 |
