линейная алгебра контрольная работа. линейная алгебра Мурашова. Задача Найти сумму матриц 1 A B Сумму матриц находим по формуле ABc a B
 Скачать 25.28 Kb. Скачать 25.28 Kb.
|
ВЫПОЛНЕНИЕ ПРАКТИЧЕСКИХ ЗАДАНИЙ ПО ДИСЦИПЛИНЕ: Линейная алгебра Группа ПМ20Э371 Студент Я.В Мурашова МОСКВА 2021 Задача 1. Найти сумму матриц 1.1 A= 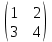 B=  Сумму матриц находим по формуле A+B=C A+B=   = =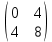 1.2 A= 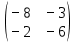 B=  Сумму матриц находим по формуле A+B=C A+B=  Найти произведение матриц 2.1 A= 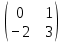 B= B= A*B= 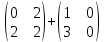 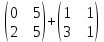 = =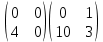 = =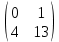 2.2 A= 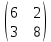 B= B= A*B=  = =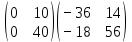 = =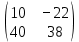 Найти определители матриц 3.1 A=  Определители матриц находим по формуле А=2*2 А=3*3-2*1=9-2=7 3.2 А= 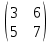 Определители матриц находим по формуле А=2*2 А=3*7-5*6=21-30=-9 Решить систему уравнений. 4.1 Дано: 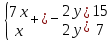 Решаем в матричном виде методом Гаусса 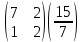 1 строку делим на 7 2 строку делим на 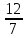 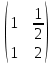 / / 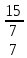  От 1 строки отнимаем 2* 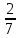 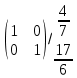 Ответ:  4.2 Дано:  Из первого уравнения выразим х 9x=11y+5 Разделим обе части на множетели при х  = = =2c= =2c=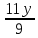 + +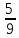 Подставим найденное в х в 2 уравнение 6у=12х-8 Получим: 6у=12*  + +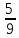 -8; далее 6у= -8; далее 6у= Разделим обе части на множетели при у: У=  =- =- =у= =у= Т.к х= 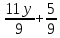 Х=  + +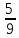 =х= =х= Для заданных векторов найти смешанное произведение 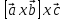 5.1  =(2;1;-2), =(2;1;-2),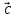 =(1;1;1) =(1;1;1)Решать будем по матричной формуле С*(a*b)= 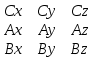 Cоответственно:1*(-2)*(-2)+1*1*2+1*1*1-1*(-2)*2-1*1**(-2)-1*1*1= 4+2+1+4+2-1=12 5.2 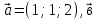 =(1;-1;3), =(1;-1;3),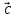 =(-2;-2;2) =(-2;-2;2)Решать будем по матричной формуле С*(a*b)= 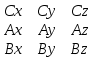 Соответственно:(-2)*1*3+(-2)*2*1+2*1*(-1)-2*1*1-(-2)*1*3-(-2)*2*(-1)= =-6-4-2-2+6-4=-12 |
