математика 6 вариан. Контрольная работа по дисциплине " Математика" 6 вариант Исполнитель студентка гр. Гмус 15 тв оюн Чодураа Сергеевна

• Название: Контрольная работа по дисциплине " Математика" 6 вариант Исполнитель студентка гр. Гмус 15 тв оюн Чодураа Сергеевна
• Дата: 29.04.2022
• Размер: 168 Kb.
• Имя файла: математика 6 вариан.doc
• Тип: Контрольная работа; #504786

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФГБОУ ВПО «УРАЛЬСКИЙ ГОСУДАРСТВЕННЫЙ ЭКОНОМИЧЕСКИЙ УНИВЕРСИТЕТ»

Центр дистанционного образования

КОНТРОЛЬНАЯ РАБОТА
по дисциплине " Математика"

№ 6 вариант


Исполнитель: студентка гр. ГМУс- 15 ТВ

Оюн Чодураа Сергеевна


Екатеринбург

2016

Тема 1. Матрицы и определители

1. 
   Вычислить определитель
   

1.2. Найти обратную матрицу для матрицы А и сделать проверку.





Проверка:

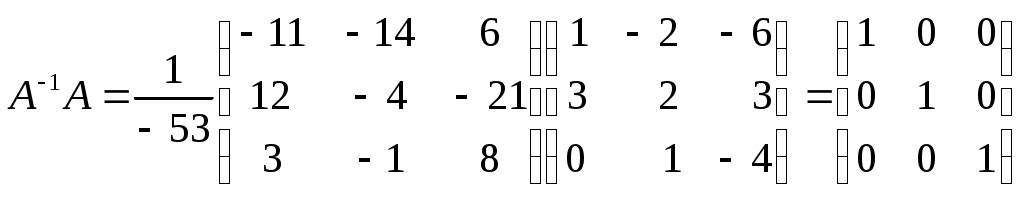Тема 2. Системы линейных уравнений

Решить систему уравнений тремя способами: методом обратной матрицы, методом Гаусса или методом Жордана–Гаусса.

1. 
   Метод обратной матрицы
   

2. 
   Метод Гаусса
   

3. 
   Метод Жордана-Гаусса
   

Тема 3–4. Векторная алгебра. Уравнение прямой

По координатам вершин треугольника ABC найти:

1. 
   периметр треугольника;
   
2. 
   уравнения сторон AB и BC;
   
3. 
   уравнение высоты AD;
   
4. 
   угол ABC;
   
5. 
   площадь треугольника.
   
6. 
   Сделать чертеж.
   

А(0; 0); В (8; 2); С(–2; 6).

1. 
   
   

2. 
   
   
3. 
   Т.к. знаем координаты A, осталось найти направляющий вектор для AD, а он перпендикулярен BC, поэтому найдем из скалярного произведения:
   

(-10; 4)(4; 10)= - 40 + 40 = 0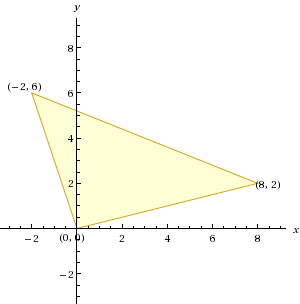

4. 
   
   
5. 
   
   

Тема 4. Уравнение плоскости

Даны точки М₁ и М₂.

Составить уравнение плоскости, проходящей через точку M₁ перпендикулярно вектору

Найти отрезки, отсекаемые данной плоскостью на осях координат. Начертить эту плоскость.

М₁ (2; –1; 5); М₂ (–2; 1; 3).

1. 
   общий вид уравнения плоскости, т.е. надо найти 4 коэффициента.
   

т.к это нормаль к плоскости, то она параллельна .

Без ограничения общности можно взять так:



Найдем d, подстановкой М₁ в уравнение плоскости



Плоскость имеет вид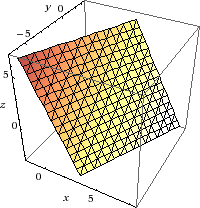

2. 
   
   
3. 
   
   

Тема 5. Линии второго порядка

Найти координаты вершин, оси, фокусы и эксцентриситет эллипса. Сделать чертеж.

9x² + 16y² = 144.

уравнение эллипса

a = 4, b = 3

Тема 6. Пределы функций

Вычислить пределы.

а)

б)

в)

Тема 7. Основы дифференцирования

Найти производную сложной функции

Тема 8. Исследование функций

Исследовать функцию и построить ее график.



Область определения:


Корни:
Корней не существует.
Непрерывность: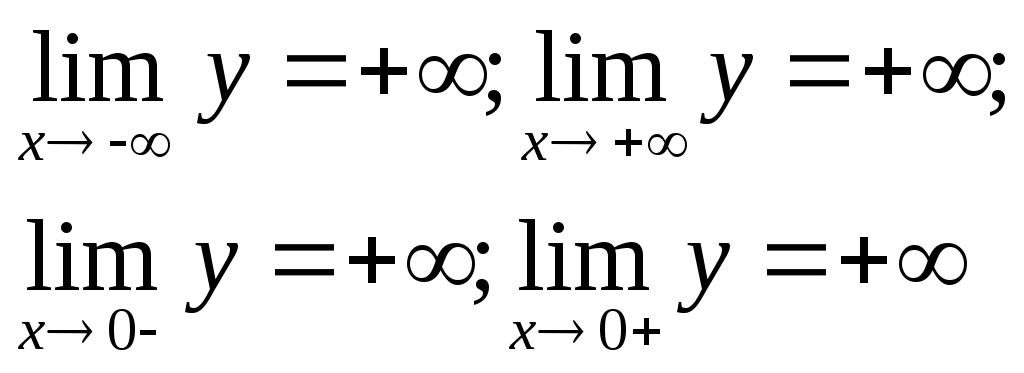

Разрыв второго порядка в точке .
Экстремум:




Выпуклость, вогнутость:

Выпукла при ,т.е.

Вогнута при ,т.е