Шпаргалка по оптике. 1. Геометрическая оптика

• Название: 1. Геометрическая оптика
• Анкор: Шпаргалка по оптике.doc
• Дата: 16.10.2017
• Размер: 1.22 Mb.
• Имя файла: Шпаргалка по оптике.doc
• Тип: Документы; #9430
• Категория: Физика
• страница: 2 из 7

Рис.5. Схема возникновения Рис.6. Учет деформации

колец Ньютона линзы

Тёмные кольца образуются там, где оптическая разность хода равна нечётному числу полуволн: ∆ = 2d + λ /2 = (2m + 1) λ /2, (24)

т.е. при толщине зазора d = m λ /2 , (25) где m = 0,1,2,3... - номер кольца.

Радиус m-ного темного кольца (r_m ) определяется из треугольника AОС (см.рис.5) r_m^{2 =} R² - (R - d,)² = 2Rd – d ², (26)

где R - радиус кривизны линзы. Полагая величину воздушного зазора в месте возникновения колец малой, (т.е. d « R) можно записать: r_m ² = 2Rd. (27)

Из этой формулы видно, что радиус кривизны линзы можно найти, измерив радиус кольца Ньютона и величину воздушного зазора в месте возникновения кольца. Радиус колец Ньютона можно измерить, воспользовавшись микроскопом, имеющим измерительную шкалу. Чтобы не измерять величину зазора (кстати, не понятно, как это сделать экспериментально), можно воспользоваться интерференционным условием возникновения темных колец (24).

Тогда радиус кривизны линзы можно выразить через радиус кольца Ньютона, длину волны используемого света и номер измеряемого кольца: r_m² = Rmλ (28)

В реальном эксперименте в формулу (27) вместо толщины воздушного зазора (d) необходимо подставить сумму толщины воздушного зазора и величины деформации линзы и стеклянной пластинки (d + δ). Учитывая, что условие возникновения темного кольца (24) определяется лишь толщиной зазора, получим следующую формулу, связывающую радиусы колец Ньютона с радиусом кривизны линзы: r_m² = Rmλ + 2Rδ (29)

Экспериментально удобнее вместо радиуса кольца Ньютона измерять его диаметр (D_m ). В этом случае формула (29) будет иметь вид: D _m² = 4Rmλ + 8Rδ, (30)

Из (30) видно, что квадрат диаметра кольца Ньютона (D_m²) пропорционален порядковому номеру кольца (m). Если построить график зависимости D_m² = f(m), то экспериментальные точки должны лежать на одной прямой, и тангенс угла наклона этой прямой (α) будет равен 4Rλ. Таким образом, для нахождения радиуса кривизны линзы необходимо, используя график зависимости D_m² = f(m), найти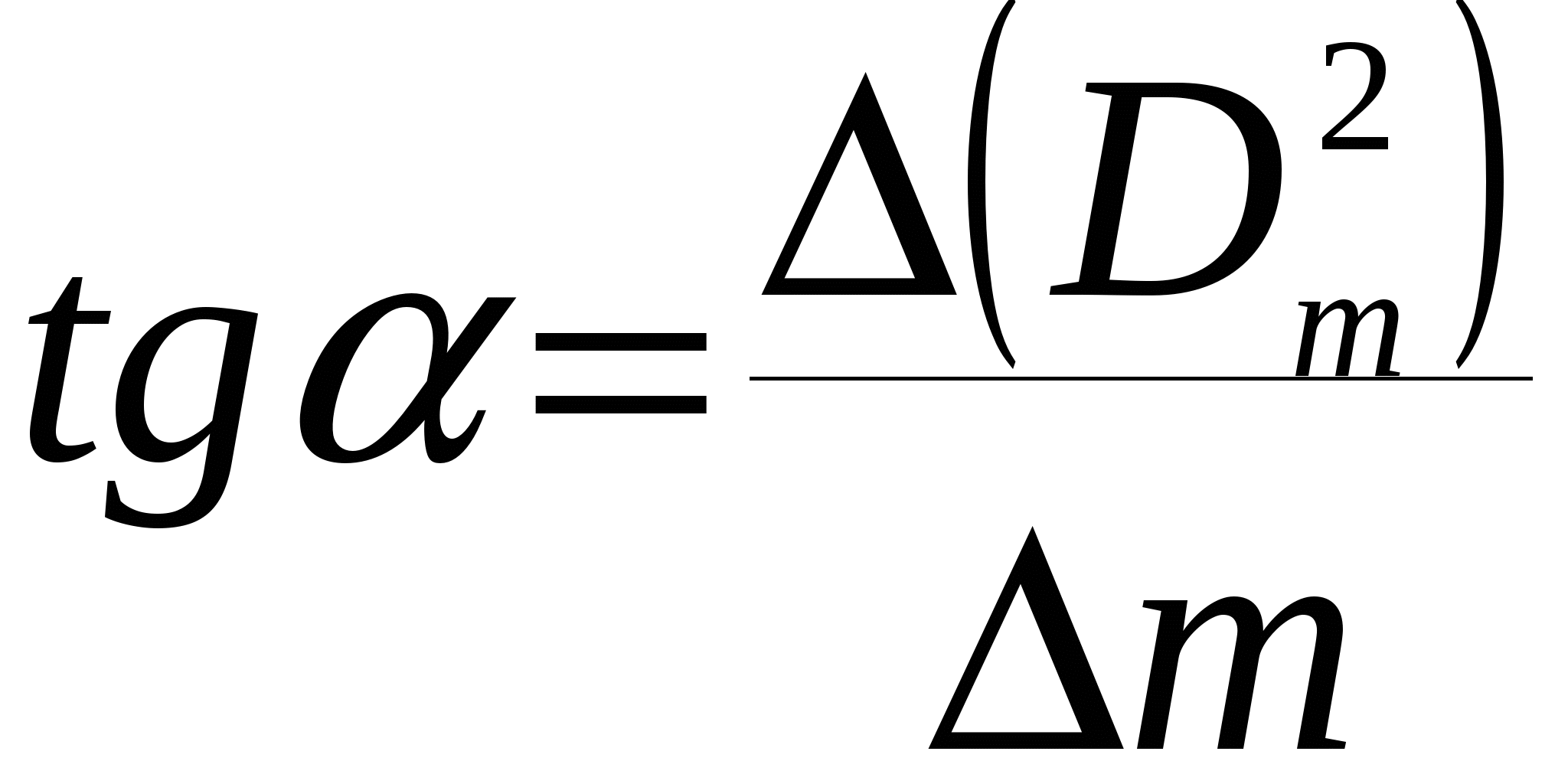

(31)

а затем рассчитать радиус кривизны линзы по формуле:

R=tgα/4λ (32)

Вследствие деформации в центре линзы наблюдается круглое темное пятно, соответствующее нулевой толщине воздушного зазора. Измерив диаметр центрального темного пятна (кольца Ньютона, номер которого m = 0), можно найти величину деформации линзы по формуле: δ= D₀²/8R (33)
Просветление оптики.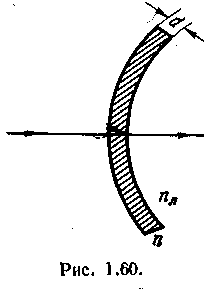

Практическое применением ин­терференции является так называемое «просветление оптики». Дело в том, что не весь световой поток, падающий на лин­зу или призму, проходит внутрь последней, а часть его отражается обратно. Сов­ременные точные оптические приборы со­держат большое количество линз, и частич­ное отражение света на многочисленных поверхностях раздела заметно снижает ин­тенсивность света, доходящего до глаза на­блюдателя или регистрирующего прибора. Помимо уменьшения яркости окончатель­ного изображения, отражение света от входного объектива наблю­дательного прибора в военном деле является причиной еще одной, неприятности. Отраженный от объектива свет («блик») возвраща­ется к противнику, демаскируя положение наблюдательного прибора.
Для уменьшения отражения света И. В. Гребенщиковым с сот­рудниками была разработана технология покрытия наружных поверхностей линзы специальными тонкими пленками. Идея метода понятна из схемы рис. 1.60. Передняя поверхность линзы покрыта специальной прозрачной пленкой. При наличии пленки падающий свет отражается дважды: от границы воздух — плен­ка и от границы пленка — линза. Показатель преломления и толщина пленки dподбираются так, чтобы оба отраженных луча были в противоположной фазе и гасили друг друга. При этом полностью исчезают блики. Поскольку же при интерференции энергия света не исчезает, а лишь перераспределяется в простран­стве, то гашение отраженного луча сопровождается соответствен­ным увеличением интенсивности преломленного луча, проходящего внутрь оптической системы.
Для того чтобы условия отражения (потеря полволны) на обеих границах раздела были одинаковы, показатель преломления плен­ки п должен быть промежуточным между единицей и показателем преломления линзы п_л. Для взаимного гашения отраженных лу­чей их оптическая разность хода 2dnдолжна быть равна половине К длины волны Следовательно, толщина пленки определится из,условия (12.1) где λ, — есть длина волны света в веществе пленки. Расчет показывает, что наиболее полное гашение будет при условии, что (12.2)

Формула (12.1) показывает, что нельзя добиться одновремен­ного, гашения для всех длин волн видимого спектра. Поэтому условие гашения (12.1) должно быть выполнено, во всяком случае, для наиболее воспринимаемой человеческим глазом длины волны λ₀=555
Практические применения интерференции. Интерферометры

Одно из практических применений интерференции — это прецизионные измерения, главным образом линейных разме­ров. Для этого служат приборы, называемые интерферо­метрами. Приведем схематическое описание некоторых основ­ных типов интерферометров.
В 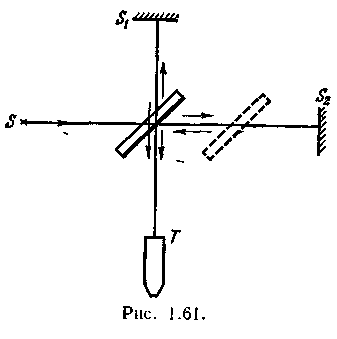интерферометре Майкельсона, изображен­ном на рис. 1.61, параллельный пучок лучей от источника S па­дает под углом 45^s на плоскопараллельную стеклянную пластин­ку. Сторона пластинки, удаленная от S, посеребренная и полу­прозрачная, разделяет луч на два части. Отраженный луч идет к зеркалу S_l( отражается от него и, возвращаясь обратно, проходит вновь^ через пластинку и попадает в зрительную трубу Т. Второй луч идет к зеркалу S_z, отражается от него, возвращается обратно и, отражаясь от пластинки, попадает в ту же трубу Т, интерфери­руя с первым. Первый из лучей дважды проходит всю толщу стек­лянной пластинки (туда и обратно). Поэтому для компенсации воз­никающей разности хода надо на пути второго луча поместить точно такую же пластинку из того же сорта стекла, показанную на рисунке пунктиром.
В зависимости от разности хода обоих лучей зрительное поле трубы Т окажется светлым или темным. При перемещении зеркала S₂ на расстояние, равное -j-, разность хода обоих лучей увеличится на -у и произой­дет смена освещенности зритель­ного поля. Более чувствитель­ным является следующий ме­тод. Неподвижное зеркало 5, чуть наклоняется. Лучи, падающие на разные точки 8_г, прохо­дят различные пути. Поэтому в окуляре будет наблюдаться ,уже не однородный фон, но система параллельных темных и светлых линий — «полосы .равной толщины», отвечающие равно­удаленным от неотклоненного положения точкам зеркала. Сме­щение S₂ вызовет перемещение этих полос, за которым легко следить с большой точностью. Таким путем был впервые измерен и сравнен с длиной стандартной световой волны международный эталон метра.
Возможность выполнять такие сравнения с очень высокой сте­пенью точности привела к тому, что световую волну сделали те­перь эталоном длины.


З.Дифракция света.Принцип Гюйгенса-Френеля. Дифракция Френеля. Метод зон Френеля. Дифракция Френеля на простейших преградах (круглом отверстии, крае полуплоскости). Спираль Корню. Дифракция Фраунгофера на щели и на системе щелей. Дифракционные решетки. Разновидности дифракционных решеток {амплитудные, фазовые, пропускающие, отражающие). Особенности изготовления дифракционных решеток, реплики Применение дифракционных решеток.
Дифракция света. Принцип Гюйгенса-Френеля. Дифракция Френеля. Метод зон Френеля. Дифракция Френеля на простейших преградах (круглом отверстии, крае полуплоскости).

П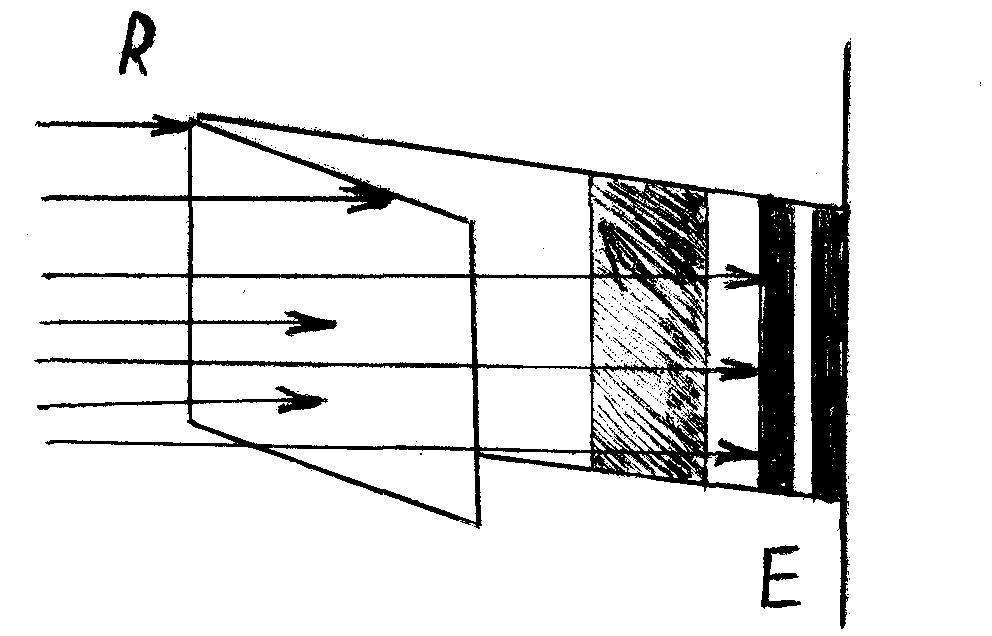оместим на пути параллельного пучка света плоскость и будем наблюдать дальнейший ход спространения световых лучей на экране Е. Если бы волна представляла собой действительно пучок параллельных прямых, то тень от объекта, поставленного на пути её распространения, должна бы иметь на экране совершенно четкие контуры. Это было предсказано геометрической оптикой и подтверждено грубыми опытами.

Это "явление огибания" края препятствия волной называется дифракцией и проявляется всякий раз, когда на пути распространения фронт волны тем или иным способом ограничивается.

Явление дифракции, которое не могла объяснить геометрическая оптика, находится в тесной связи с явлением интерференции и может быть объяснено на основании принципа Гюйгенса.
Р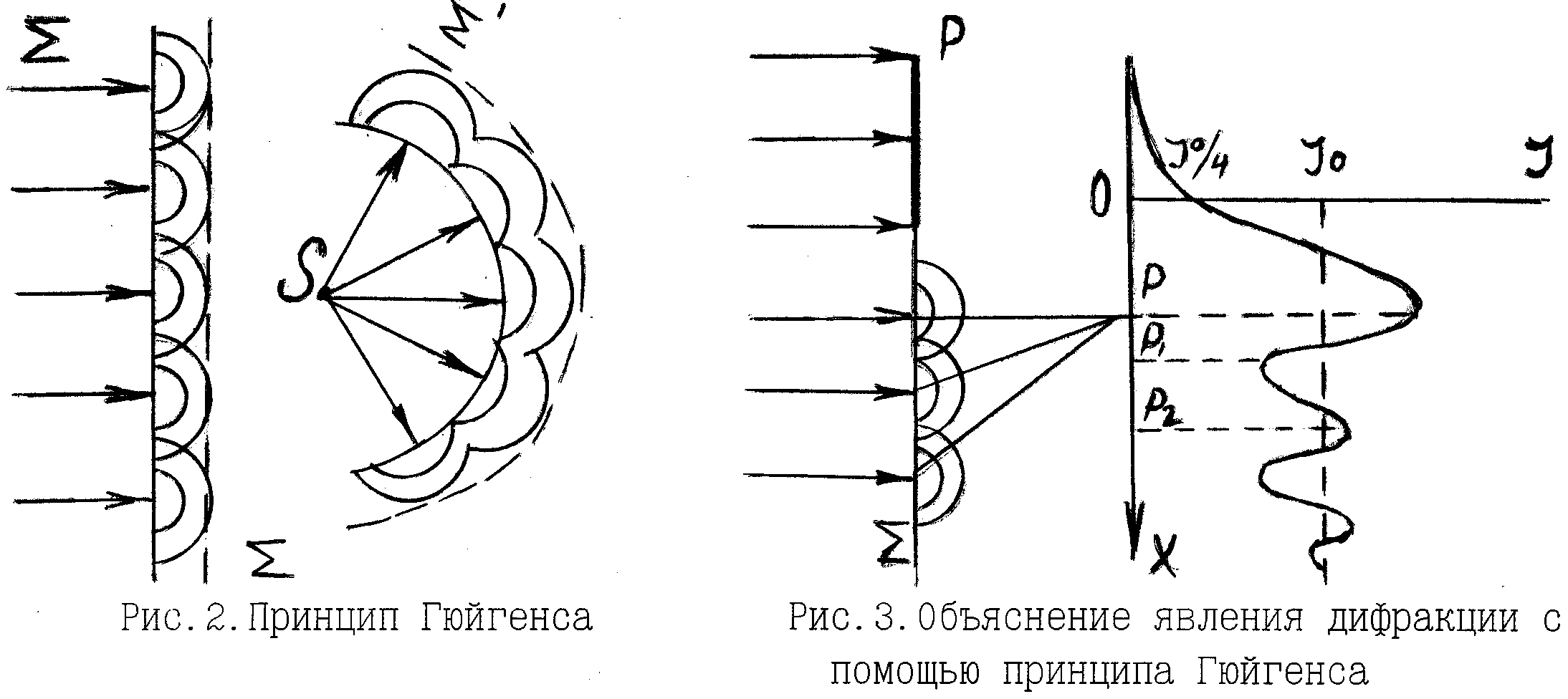
ис.1. Вид дифракционной картины от плоскости ьСогласно принципу Гюйгенсу каждую точку волновой поверхности следует рассматривать как источник элементарных сферических волн, огибающая их поверхность служит новой волновой поверхностью (рис.2 ).

Объясним явление дифракции на краю плоскости Р, проиллюстрированное на рис.1, на основании принципа Гюйгенса.

Волновая поверхность Σ является источником вторичных сферических волн (рис.3). Каждая точка поверхности Σ эмитирует световые волны в различных направлениях. Выберем те лучи, которые собираются в точке экрана. Эти лучи когерентны, т.е. имеют одинаковую частоту, постоянную разность фаз, следовательно, могут интерферировать. Если лучи приходят в точку Р в фазе, то происходит усиление света и мы наблюдаем световую полосу. В некоторую точку P₁ лучи приходят в противофазе и происходит взаимное ослабление света. Тогда в точке Р₁ мы наблюдаем тёмную полосу и т.д. Аналогично можно объяснить явление дифракции на щели на круглом отверстии и на других преградах.
Спи­раль Корню.

На рис. 128.8, б показаны только колебания, обусловленные зонами, лежащими справа от точки Р. Зоны с номерами т к т' расположены симметрично отно­сительно Р. Поэтому естественно при построении диаграммы векторы, изображающие соответст­вующие этим зонам колебания, располагать симметрично относи­тельно начала координат О (рис, 128.9). Если ширину зон устре­мить к нулю, ломан-ая линия, изображенная на рис. 128.9, превратится в плавную кривую (рис. 128.9), которая называется спи­ралью Корню.

Уравнение спирали Корню в параметрической форме имеет вид

(128.8)

Эти интегралы называются интегралами Френеля. Они не берутся в элементарных функциях, однако имеются таблицы, по которым можно находить значения интегралов для разных v. Смысл параметра у заключается в том, что \v\ дает длину дуги кривой Корню, измеряемую от начала координат.

Числа, отмеченные вдоль кривой на рис. 128.9, дают значения параметра v. Точки F₁и f₂, к которым асимптотически приближа­ется кривая при стремлении vк +∞ и -∞, называются фоку­сами или полюсами спирали Корню.
Дифракция Фраунгофера от щели

Пусть на бесконечно длинную щель падает плоская световая юлна (рис. 129.1). Поместим за щелью собирающую линзу, а в фокальной плоскости линзы — экран. Волновая поверхность падаю­щей волны, плоскость щели и экран па­раллельны друг другу. Поскольку щель бесконечна, картина, наблюдаемая в любой плоскости, перпендикулярной к щели, будет одинакова. Поэтому доста­точно исследовать характер картины в одной такой плоскости, например в пло­скости рис. 129.1. Все вводимые в даль­нейшем величины, в частности угол φ, образуемый лучом с оптической осью линзы, относятся к этой плоскости.

bsinφ=±kλ (k=1,2,3..) – минимумы интенсивности.

Дифракция на дифракционной решетке Пропускающие решетки. Отражательные решетки.

Дифракционной решеткой называется совокупность большого числа одинаковых, отстоящих друг от друга на одно и то же рас­стояние щелей (рис. 130.1). Расстояние dмежду серединами со­седних щелей называется периодом решетки.

Р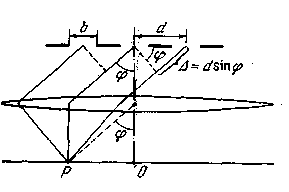асположим параллельно решетке собирательную линзу, в фо­кальной плоскости которой поставим экран. Выясним характер ди­фракционной картины, получающейся на экране при падении на решетку плоской световой волны (для простоты будем считать, что волна падает на решетку нормально). Каждая из щелей даст на эране картину, описываемую кривой, изображенной на рис. 129.3. Картины от всех щелей придутся на одно и то же место экрана (независимо от положения щели, центральный максимум лежит против центра линзы). Если бы колебания, приходящие в точку Р от раз-. личных щелей, были некогерентными, результирующая картина от N щелей отличалась бы от картины, создаваемой одной щелью, лишь тем, что все интенсивности возросли бы в N раз. Однако коле­бания от различных щелей являются в большей или меньшей сте­пени когерентными; поэтому результирующая интенсивность будет отлична от NI_Ф (I_ф — интенсив­ность, создаваемая одной щелью; см. (129.6)).

В дальнейшем мы будем пред­полагать, что радиус когерентно­сти падающей волны намного пре­вышает длину решетки, так что колебания от всех щелей можно считать когерентными друг относительно друга.

Таким образом мы имеем максимум дифракции ( светлые полосы ) для направлений, удовлетворяющих условию:

d · sin φ = ±m · λ (2), где m - порядок спектра, φ - угол дифракции.
Таким образом мы имеем минимум дифракции ( тёмные полосы ) для направлений, удовлетворяющих условию:

b · sin φ = ±k · λ (3), m - порядок спектра, φ - угол дифракции.
По устройству дифракционные решетки бывают про­пускающие и отражательные. Пропускающие решеткиизготавливаются из стеклянных или кварцевых пластин путем нанесения алмазным резцом ряда параллельных штрихов. Промежутки между штрихами являются щеля­ми. Отражательные решеткиизготавливаются нанесением алмазным резцом штрихов на поверхности металличеcкого зеркала. Лучшие решетки содержат 1200 штрихов на 1 мм решетки. Общее число штрихов у таких решеток длиной порядка 200 мм достигает 200 тысяч.
4.Фотометрия и термодинамика излучения.Основные фотометрические величины (поток лучистой энергии, сила света, яркость, освещенность). Источники Ламберта. Особенности восприятия излучения человеческим глазом. Фотометрические и светотехнические величины. Функция видности. Тепловое излучение. Закон Кирхгофа. Энергетическая светимость. Испускательная и поглощательная способность тела. Абсолютно черное тело. Законы излучения абсолютно черного тела (формула Планка, закон Стефана-Больцмана, закон Вина) Оптическая пирометрия Методы оптического измерения температуры.
Фотометрические величины и единицы. Источники Ламберта.

Фотометрией называется раздел оптики, занимающийся изме­рением световых потоков и величин, связанных с такими потоками.

Сила света. Источник света, размерами которого можно пре­небречь по сравнению с расстоянием .от места наблюдения до ис­точника, называется точечным. В однородной и изотропной среде волна, излучаемая точечным источником, будет сферической. Для характеристики точечных источников света применяется сила света /, которая определяется как поток излучения ис­точника, приходящийся на единицу телесного угла:

(114.1)

(dФ — световой поток, излучаемый источником в пределах телес­ного угла dQ). Для изотропного источника

(114.2)

где Ф — полный световой поток, излучаемый источником по всем направлениям.

В случае протяженного источника можно говорить о силе света элемента его поверхности. Тогда подв формуле (114.1) сле­дует понимать световой поток, излучаемый элементом поверхно­сти dSв пределах телесного угла

Единица силы света — кандела (кд) является одной из ос­новных единиц Международной системы (СИ). Ее значение при­нимается таким, чтобы яркость (см. ниже) полного^лизлучателя при температуре затвердевания платины была равна 60 кд на 1 см². Под полным излучателем понимается устройство, обладающее свойствами абсолютно черного тела (см. т. 3).

Световой поток. Единицей светового потока является люмен (лм). Он равен световому потоку, излучаемому изотропным источ­ником с силой света в 1 кд в пределах телесного угла в один сте­радиан:

(114.3)

Опытным путем установлено, что световому потоку в 1 лм, обра­зованному излучением с длиной волны А, = 0,555 мкм, соответст­вует поток энергии в 0,0016 Вт. Световому потоку в 1 лм,-образо­ванному излучением с другой Я, соответствует поток энергии

(114.4)