Ответы(Схем)11-20. Полным дешифратором называется устройство, имеющее
 Скачать 1.11 Mb.
|
d[1] & d[0] ;//6 assign q[1] = |
d0
0
DC
0
1
q
d1
q
1
2
q
3
5.6) учитывается физика его работы. В столбце «hex»
приведены значения выходного кода в 16-ричной системе, что
Таблица
5.6.
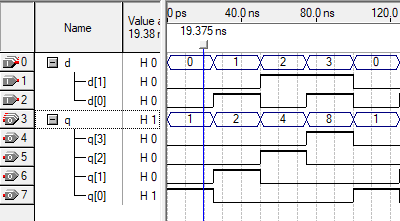
Таблица истинности позволяет записать логические функции для каждого выходного сигнала.
| d1d0 | q3q2q1q0 | hex |
| 0 0 | 0 0 0 1 | 1 |
| 0 1 | 0 0 1 0 | 2 |
| 1 0 | 0 1 0 0 | 4 |
| 1 1 | 1 0 0 0 | 8 |
;
q0
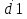
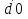.q1 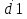d0 . q2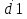 
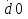; q3 d1 d0 .По данным формулам несложно составить схему (Рис. 5.24) и описание на Verilog (Пример 5.4.). В схеме дешифратора для формирования каждого выходного
//Пример 5.10. Дешифратор module v510_dc (a, q); //2
input [1:0] d; //3
output [3:0] q; //4 assign q[3] = d[1] & d[0] ; //5 assign q[2] = d[1] &
| | 1 | q |
| d2 | ||
| | ||
| |
d3 1
d3
&
d2 d1d3
1
d2 g
1
q0 d1 d0
Рис. 5.28 Обозначение шифратора
Рис. 5.29 Схема шифратора
Таблицу истинности для шифратора в простейшем случае можно получит
Таблица 5.8.
из таблицы 5.6, поменяв местами входы и выходы. В реальных условиях, при воздействии помех, может быть возбуждено несколько входных проводников. Поэтому схему шифратора усложняют, делают ее приоритетной (Таблица 5.8). Приоритетный шифратор вырабатывает на выходе двоичный номер старшего запроса. При наличии всего одного запроса приоритетный шифратор работает так же, как и двоичный. В интегральном исполнении изготавливают,
| d3 | d2 | d1 | d0 | q1 | q0 | g |
| 1 | х | х | х | 1 | 1 | 1 |
| 0 | 1 | х | х | 1 | 0 | 1 |
| 0 | 0 | 1 | х | 0 | 1 | 1 |
| 0 | 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
как правило, приоритетные шифраторы. В приведенной таблице d3..d0 – входные сигналы, q1..q0 – выходной код, g – выходной сигнал, отмечающий наличие запросов.
По таблице записаны формулы для выходных сигналов, для упрощения
которых, использовано тождество: a a x a x.
В соответствии с таблицей истинности построены временные диаграммы, поясняющие работу приоритетного шифратора (Рис.5.30), предназначенные для его тестирования.d 0 1 2 3 4 5 6 7 8 9 A B C D E F t
q
0
1
2
3
t
Рис. 5.30 Работа приоритетного шифратора
//Пример 5.10. Дешифратор
module v510_dc (a, q,q1); //2
[3:0] d; //3
input [1:0] q; //4
input q1; //5
assign q1 = d[3] | d[2] | d[1] | d[0] ;//6
assign q[1] = d[3] | d[2] ;//7
assign q[0] = d[3] | d[2] & d[1] ;//8
endmodule //9
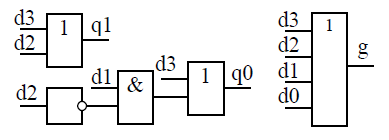
13. Дешифратор - демультиплекмор, назначение, принцип работы, синтез (таблица истинности, логические функции, схема, временные диаграммы, описание на языке Verilog) типы, применение.
Дешифратор, дополненный общим разрешающим входом, называется дешифратором – демультиплексором (Рис.5.26).
Наличие дополнительных входов разрешения, которых может быть
несколько, позволяет разрешать, или запрещать работу устройства. Для того, чтобы входные сигналы (d1, d0) вызывали изменения выходных сигналов (q3..q0), необходимо подать разрешающий сигнал e=1. В этом случае, как и в предыдущей схеме, на одном из выходов, номер которого определяет адрес, формируется сигнал, равный 1. При е=0 все выходные сигналы запрещены, и равны нулю.
a0 a1
е
q0 q1 q2 q3
е
0
1
2
3
DC
0
1
е q0
q1
q2 q3
Рис.5.26
Дешифратор - демультиплексор
a1 a0
Рис.5.27. Пояснение
работы демультиплексора
| е | d 1 | d0 | q3 | q2 | q1 | q0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 | 0 | 0 | 0 |
В названии схемы отражена возможность ее применения в качестве демультиплексора, что поясняет рис. 5.27.
Демультиплексоры выполняют функцию, обратную мультиплексорам, они производят коммутацию одного информационного входного сигнала на 2mвыходов, где m- число адресных входов. При этом в качестве информационного входа демультиплексора используется разрешающий вход «е».
Таблица истинности для дешифратора- демультиплексора (таблица 5.7) позволяет разработать его схему и составить описание.
Выходы и разрешающие входы дешифраторов, выполненных интегрально, могут быть инверсными. Так, например, дешифратор-демультиплексор с инверсными выходами и инверсным разрешающим входом
CSформирует при CS=0 нулевой логический сигнал на одном из выходов, в соответствии с адресом на входах. При CS=1 все выходные сигналы равны 1.
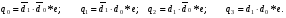
5.10. Дешифратор-Демультиплексор module v510_dc (a, q, e); //2
input [1:0] d; //3
output [3:0] q; //4
assign q[3] = d[1] & d[0] & e ; //5
assign q[2] = d[1] & d[0] & e; //6
assign q[1] = d[1] & d[0] & e;//7
assign q[0] = d[1] & d[0] & e;//8
endmodule //9
Рис. 5.36. Компаратор кодов
Данная логическая функция позволяет составить схему, формирующую признак равенства кодов, а также описание на языке Verilog (Пример 5.13).
Для построения схемы сравнения положительных чисел, представленных в прямом коде без знака, и формирующей признак G, необходимо сравнить коды чисел, начиная со старшего разряда.
Признак G будет равен 1, если в старшем разряде числа А записана 1, а в старшем разряде числа В записан 0, остальные разряды на результат уже не влияют. Если старшие разряды равны, то значение признака будут определять следующие разряды, G=1, если следующий разряд числа А - единица, а числа В - ноль . Рассуждая таким образом можно рассмотреть все разряды чисел и записать логическую функцию.
G A3 B3 E3 A2 B2 E3 E2 A1 B1 E3 E2 E1 A0 B0
Признаки равенства отдельных разрядов определяют очевидные формулы:
E3 ( A3 B3 );
E2 ( A2 B2 );
E1 ( A1 B1 );
E0 ( A0 B0 );
Полученные формулы позволяют составить схему, а также описание компаратора кодов, формирующего признак G – больше. Функциональные возможности языка Verilog позволяют составить компактное и наглядное поведенческое описание, компараторов кодов, в в которых используются операторы сравнения, описанные в главе 3. Операторы сравнения формируют одноразрядные сигналы - результат сравнения векторов (параллельных кодов).
//Пример 5.14. Компаратор module v514_compar ( a, b, e, g, l);
input [3:0]a, b; //3
output e, g, l; //4
assign e = a==b; //5
assign g = a>b; //6
ssign l = a
endmodule //8
Поведенческое описание компаратора, формирующего три основных признака отношения кодов – «меньше», «равно» и «больше» (Пример 5.14) составлено в соответствие с обозначением (Рис. 5.36). Входные сигналы компаратора – это 4-ех разрядные коды «а» и «b» , а выходные – признаки отношения кодов: равно «e», больше «g», меньше «l».
Теоретические временные диаграммы, поясняющие работу компаратора кодов, описанного в примере 5,15, приведены на рис. 5.37.
a
1
2
3
4
5
6
7
8
b
4
5
6
e
g
l
t t t t
t
Рис. 5.37. Работа компаратора кодов
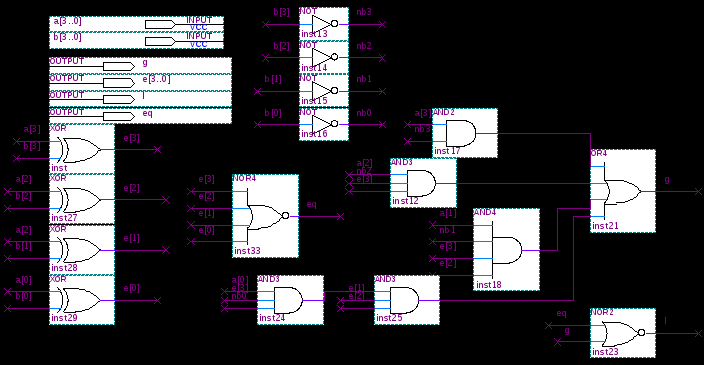
Анализ постановки задачи
Рис. 5.9.
Обозначение сумматора младшего разряда (c) (Рис. 5.9).
Выходами схемы являются сумма для данного разряда (s) и перенос в следующий разряд (p). Сумматор, имеющий три входа, называют также «полным сумматором». Включая параллельно несколько подобных схем можно получить сумматор с произвольным числом разрядов (с последовательным переносом).
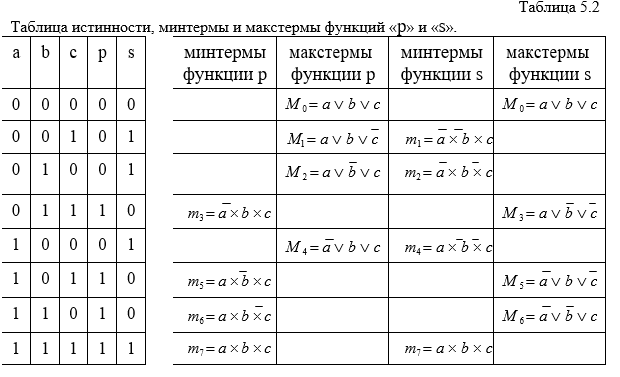
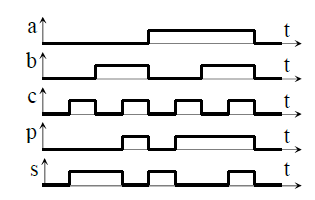
Для рассматриваемого устройства таблица истинности описывает логическую функцию трех переменных, следовательно, количество наборов входных сигналов, или строк таблицы равно 8. При составлении таблицы истинности (Таблица 5.2) учитываем, что значения переноса и суммы образуют двухразрядное двоичное число, равное количеству входных сигналов, равных единице. Если в строке таблицы только один из входов равен 1, то p=0, s=1; если два сигнала равны единице, то p=1, s=0;если три сигнала равны единице, то p=1, s=1.
В дополнение к таблице истинности приведены минтермы и макстермы функций «p» и «s», записанные в соответствии с правилами, рассмотренными в главе 4.
Составление логических функций
Логические функции в совершенной дизъюнктивной нормальной форме (СДНФ) представляет собой дизъюнкцию всех минтермов, число которых равно числу единиц логической функции в таблице истинности. Минтерм – произведение всех аргументов, записанное с соответствии с двоичным набором, на котором функция равна единице, над аргументами, которые в наборе равны нулю, в произведении ставится инверсия.
Логические функции для сигналов p и s в СДНФ имеют вид:
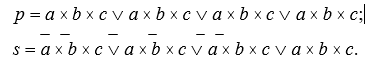
Для получения логических функций в совершенной конъюнктивной нормальной форме (СКНФ) записываются, в скобках, все макстермы и соединяются знаками умножения. Число сомножителей равно числу строк в
таблице истинности, для которых функция равна нулю. Каждый макстерм учитывает двоичный набор, на котором функция равна нулю, над аргументами, равными единице, в дизъюнкции ставится инверсия. Логические функции для сигналов p,sв СКНФ имеют вид:
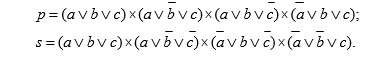
После минимизации имеем:
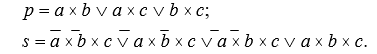
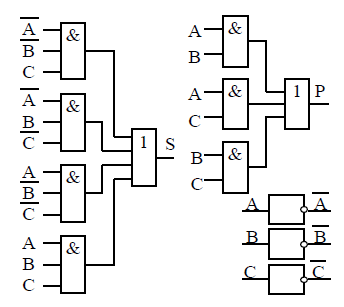
Схема устройства строится по минимизированным логическим функциям (Рис. 2.11). В соответствии с постановкой задачи, схема содержит три входных и два выходных терминала (a,b,c,p,s).
Схема сумматора
Для формирования выходного сигнала «s» необходимы инверсные значения входных сигналов, для их формирования используются инверторы (элементы NOT).
| a | b | p | s |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
a
b
p
s
t
t
t
t
Рис. 5.1. Полусумматор, символ, логическая функция, таблица истинности, схема, временные диаграммы, форматы данных
Проект полусумматора s51_hs по схеме (этапы 2-11) представлен на рис. 5.2.
Рис. 5.2. Схема и временные диаграммыполусумматора s21_hs
17.Многоразрядный сумматор, инкрементор, принцип работы, схема, временные диаграммы, описание на языке Verilog.
s3
a3
p
SM
a
s
b
с
p
b3
s2
a2
SM
a
s
b
с
p
b2
s1
a1
SM
a
s
b
с
p
b1
HS
a
b
s
p
s0
b0
a0
Рис. 5.8. Схема параллельного сумматора
Для суммирования двоичных чисел представленных параллельным двоичным кодом используют схемы многоразрядных сумматоров, содержащие необходимое количество одноразрядных сумматоров (Рис. 5.14).
Если входной перенос отсутствует, то в младшем разряде используют полусумматор, который суммирует входные слагаемые и формирует сумму данного разряда и перенос в следующий разряд. В остальных разрядах суммируются входные слагаемые и перенос из предыдущего разряда. В данной схеме используется последовательный перенос от разряда к разряду, поэтому схема имеет ограниченное быстродействие, которое ухудшается с увеличением разрядности. Существуют схемы с ускоренным переносом, обеспечивающие повышение быстродействия
Для построения схемы данного устройства необходимо, используя схемы
b
a
s
p
t
t
t
t
e
f
0
1
2
3
4
5
6
7
e
f
0
1
D
E
F
0
Рис. 5.9 Работапараллельного сумматора
одноразрядных полусумматора и сумматора построить схему параллельного сумматора. Процесс проектирования сокращается при использовании описания параллельного сумматора на языке Verilog (Пример 5.6).
//Поведенческое описание //параллельного сумматора
module v53_4sum (a,b,s,p); //3
input [3:0] a,b; //4
output [3:0] s //5
output p; //6
assign {p,s}=a+b; //7
endmodule //8
0
a
b
q
p
3
+
Рис. 5.10 Пояснение работы сумматора
Задание 5.4. Инкрементор
Разработайте иерархический проект 4-разрядного инкрементора.
Анализ. Инкрементор - выполняет прибавление единицы к входному коду. Для построения инкрементора в каждом разряде входного кода используется полусумматор (Рис. 2.16) .
HS
a
b
p
s
q3
q2
q1
q0
d3
d2
d1
d0
c
p
HS
a
b
p
s
HS
a
b
p
s
HS
a
b
p
s
Рис.5.17. Инкрементор, схема, символ, диаграммы, форматы данных
0
1
2
3
p
0
1
2
3
c
INC
d0
d1
d2
d3
c
q0
q1
q2
q3
p
d
c
q
p
t
t
t
t
D
E
F
0
1
1
2
3
С
D
E
F
0
1
2
3
0
d
ci
q
p
3
+
Входами инкрементора являются 4-разрядный код d[3..0], к которому прибавляется сигнал c (Carry - перенос). При c = 0 инкремента нет. Выходной код обозначен q[3..0], выходной перенос – p. Бит выходного переноса p и 4-разрядный выходной код q образуют 5-разрядное число.
//Инкрементор
module v54_inc d,c,q,p);
input [3:0] d; //3
input c ; //4
output [3:0] q; //5
output p; //6
assign {p,q} = d+c;//7
endmodule //8
Описание Инкрементора на Verilog выполнено подобно описанию сумматора как поведенческое. В операторе объединения исходные векторы записываются в фигурных скобках через запятую. Объединенный вектор может быть записан справа и слева от знака равенства в операторе присваивания. Поведение схемы описывает строка 7, структура данных показана на рис.2.16.
Создайте иерархический проект инкрементора sv24_inc для сравнения варианта, введенного в виде схемы s24_inc и в виде описания v24_inc.
18.АЛУ комбинационного типа, принцип построения, формирование признаков.
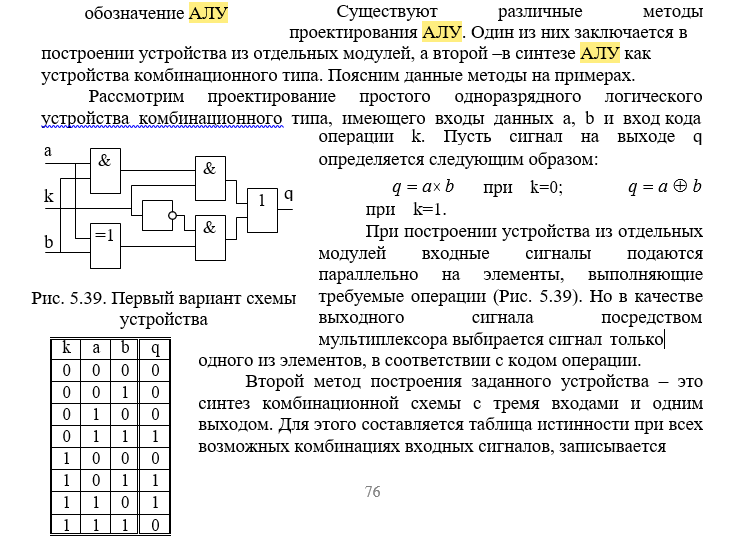
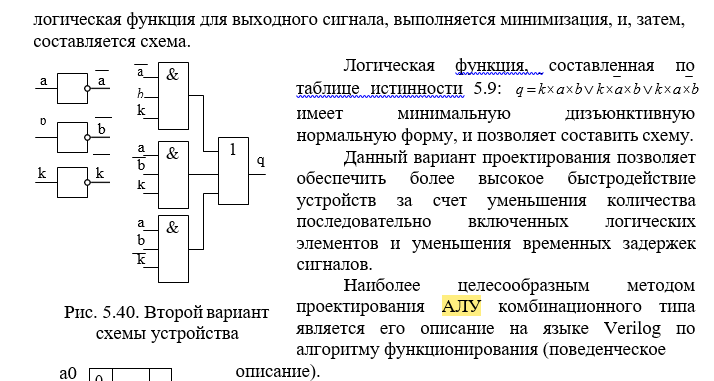
Ядром любого процессора является арифметико – логическое устройство (АЛУ), выполняющее математиченскую обработку данных. Входами АЛУ являются 4-разрядные операнды (a, b) и двухразрядный код операции (k), а выходами – 4-разрядный код результата (q) и признаки результата, наапример, перенос с и признак нуля z. (Рис. 4.4). Пусть заданы коды операций: 0 – суммирование, 1 – поразрядная логическая операция «И», 2 – поразрядная логическая операция «ИЛИ»., 3 – поразрядная логическая операция «сумма по модулю 2».
//Комбинационное АЛУ 1
module v43_alu (a,b,k,q, c);//2
input [3:0] a, b; //3
input [1:0] k ; //4
output [3:0] q; //5
output c; z; //6
assign {c,q} = (k == 0) ? (a +b):
(k==1)?( a&b):
(k==2) ? (a | b):(a ^ b); //7
endmodule //8
k=0?
0
1
1
0
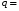
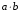
k=1?
k=2?
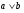
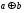
1
0
Рис. .4. Обозначение
АЛУ
4
a
b
k
q
c
z
ALU
4
2
4
0000
0001
0010
0011
0100
0101
0110
0111
0
1
2
3
0101
0110
0111
1000
1001
1010
1011
1100
0101
0111
0010
0000
1101
1111
1101
1011
t
t
t
t
a
b
q
k
Рис. 4.5. Временные диаграммы, поясняющие работу АЛУ комбинационного типа
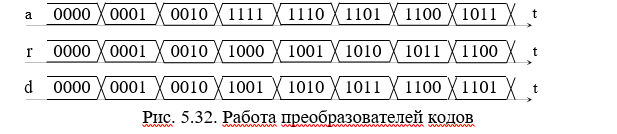
19. Преобразователи кодов: прямого в обратный и дополнительный, двоичного в код Грея, описание на Verilog.
Для представления чисел со знаком используют прямой, обратный и дополнительный коды. Знак числа отображает старший разряд, его называют знаковым. Остальные разряды, их называют значащими, отображают значение числа.
Для положительных чисел знаковый разряд равен нулю, а значащие разряды для прямого, обратного и дополнительного кодов совпадают. Отрицательные числа имеют знаковый разряд равный единице. Для получения значащих разрядов обратного кода необходимо инвертировать соответствующие разряды прямого кода.
Преобразование прямого кода в обратный код несложно выполнить посредством логических схем. Обозначим разряды прямого кода a3..a0, а обратного кода r3..r0. Соответствие между прямым и обратным кодами отображает таблица 5.8. Старший, знаковый разряд для этих кодов совпадает,
Преобразование перемещений или угла поворота в двоичный код производится с использованием специальных масок, которые имеет проводящие и непроводящие, либо прозрачные и непрозрачные участки. Выходной код снимают электрические, или оптические считывающие устройства, расположенные на одной линии, перпендикулярно дорожкам.
d3
d2
d1
d0
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
Рис. 4.4. Кодирующая маска преобразователя перемещения в двоичный код
При использовании двоичного кодирования элементов маски (Рис. 4.4), переход от одного дискретного значения к другому, когда изменяется значение нескольких разрядов, сопровождается ошибками неоднозначности. Изменение состояний отдельных разрядов не может быть одновременным из-за погрешностей изготовления маски.
11
01
00
10
011
001
000
010
111
101
100
110
Рис. 4. 5 Двумерный и
3-мерный кубы
Для устранения ошибок неоднозначности в преобразователях, а также для уменьшения помех при переключениях в цифровых схемах используют код Грея, в котором при переходе от любого состояния к следующему изменяется только один разряд . Получение последовательности чисел в коде Грея иллюстрируется геометрическими представлениями двоичных чисел, в которых отрезки имеют единичную длину, а координаты вершин образуют двоичные коды. (Рис. 4.5). Двухразрядные числа кода Грея (00 - 01 - 11 – 10) получаются при обходе контура на плоскости (двумерного куба). Именно такая последовательность кодов обозначает клетки карты Карно, при этом для соседних клеток изменяется только один разряд. Последовательность 3-разрядных чисел в коде Грея получается при обходе вершин трехмерного куба: 000 – 001 – 011 – 010 – 110 – 111 – 101 – 100.
В формулах разряды двоичного кода обозначены буквой b, а кода Грея – g.
Преобразование двоичного кода в код Грея выполняется по правилу: старшие разряды совпадают, а каждый следующий разряд кода Грея равен сумме по модулю два данного и предыдущего разрядов двоичного кода.
-
Преобразование двоичного кода
в код Грея
Преобразование кода Грея
в двоичный код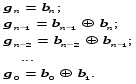
Для обратного преобразования кода Грея в двоичный код старшие разряды также совпадают, но каждый следующий двоичный разряд двоичного кода получается суммированием по модулю два всех предыдущих разрядов кода Грея.
//Дополнительный код
module grey (a, r);
input [3:0] a;
output [3:0] r;
assign r = 1’h0 – a;
endmodule
//Обратный код
module grey (a, r);
input [3:0] a;
output [3:0] r;
assign r = 1’hF – a;
endmodule
//Код Гея
module grey (b, g);
input [3:0] b;
output [3:0] g;
assign g[3]=b[3];
assign g[2] = b[3]^b[2];
assign g[1] = b[2]^b[1];
assign g[0] = b[1]^b[0];
endmodule
20. Статический асинхронный RS – триггер с установочными входами, назначение, пояснение принципа работы по схеме, таблица истинности, временные диаграммы.
Триггер - элемент памяти для хранения одного бита информации, устройство с двумя устойчивыми состояниями, Основу триггера составляет запоминающая ячейка из двух инвертирующих элементов, в которой действует положительная обратная связь, обеспечивающая наличие двух устойчивых состояний схемы.
В асинхронных триггерах запись нуля или единицы происходит под действием входного управляющего сигнала. В синхронных статических триггерах момент записи определяет уровень сигнала синхронизации. В синхронных динамических триггерах момент записи определяет изменения сигнала синхронизации – фронт или спад импульса.
Элементы И—НЕ, соединенные в замкнутую цепь, образуют
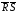-триггера. Режим хранения информации, при котором в контуре действует положительная обратная связь, возникает при подаче на оба установочных входа сигнала 1, при этом логические элементы передают сигналы положительной обратной связи. Если в режиме хранения при
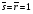предположить q=0, то комбинация входных сигналов элемента dd2 с учетом выходного сигнала элемента dd1 будет 10, а на выходе элемента dd2, в соответствии с логикой его работы, появится сигнал 
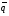= 1. Этот сигнал, поступая на вход элемента dd1, создаст комбинацию входных сигналов 11, в соответствии с которой на выходе этого элемента формируется q= 0. Значение сигнала, поступившего по цепи обратной связи, совпадает с принятым исходным значением. Таким образом, положительная обратная связь обеспечивает сохранение состояния триггера. Подобным образом можно пояснить хранение состояния q= 1.s
q
&
dd1
r
q
&
dd2
Рис. 6.1. Схема, таблица истинности и теоретические временные диаграммы асинхронного
-триггераx
t
t
t
t
t0
x
t1
t2
t3
t4
t5
s
r
q
q
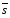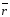 |  | qn | qn+1 | Режим |
| 1 | 1 | 0 | 0 | Хранение |
| 1 | 1 | 1 | 1 | |
| 0 | 1 | 0 | 1 | Установка 1 |
| 0 | 1 | 1 | 1 | |
| 1 | 0 | 0 | 0 | Установа 0 |
| 1 | 0 | 1 | 0 | |
| 0 | 0 | 0 | х | Запрещенная комбинация |
| 0 | 0 | 1 | х |
Установочные входы в этом триггере являются инверсными, поэтому в их обозначениях использован знак инверсии. Для установки q = 1 необходимо подать сигнал 0 на вход
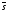.- это установочный вход единицы, а для установки q = 0 - подать 0 на установочный вход нуля 
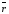. и Одновременная подача сигналов установки q = 1 и q = 0 запрещена. Работу триггера описывают таблица истинности и теоретические временные диаграммы (рис. 6.1). Входные сигналы триггера разработаны для иллюстрации определенных режимов работы. На диаграммах отмечены моменты времени: t0 – режим хранения (
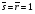), t1 – установка 1 (
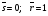), t2 – подтверждение состояния 1 (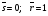), t3 – установка 0 (
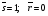), t4 – запрещенная комбинация входов (
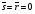), t5 – вновь режим хранения.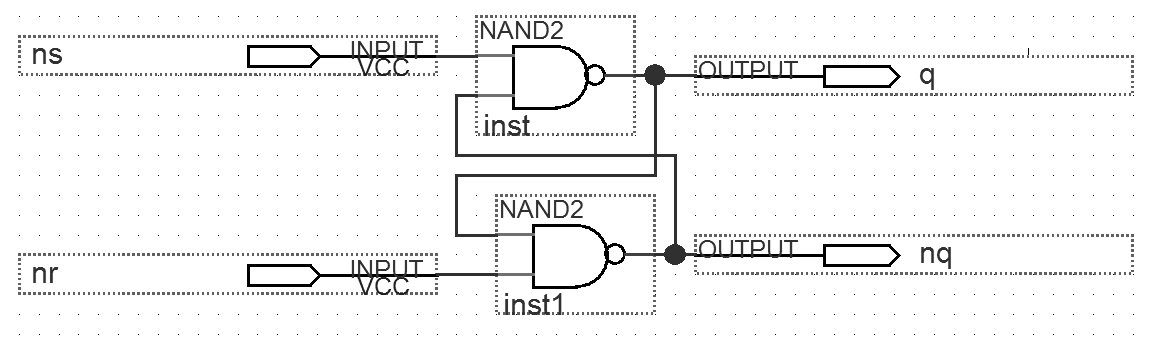
Рис. 6.2. Схема s61_nrns в редакторе
Рис. 6.3. Моделирование схемы s61_nrns
module rstrigger (ns, nr,q);
input ns, nr;
output q;
reg q;
always
case ({ns,nr})
2'b00: q=q;
2'b01: q=1'b1;
2'b10: q=1'b0;
2'b11: q=1'bx;
endcase
endmodule