Контрольная по физике 2 курс. Физика_КР№ 4. Решение На основании первого закона Вина (закона смещения)
 Скачать 253.33 Kb. Скачать 253.33 Kb.
|
|
Задача № 409 Температура абсолютно черного тела 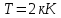 . Определить длину волны . Определить длину волны 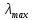 , на которую приходится максимум энергии излучения, и , на которую приходится максимум энергии излучения, и 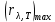 спектральную плотность энергетической светимости для этой длины волны. спектральную плотность энергетической светимости для этой длины волны.
где 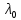 - длина волны, на которую приходится максимум спектральной плотности излучательности, - длина волны, на которую приходится максимум спектральной плотности излучательности, 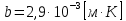 - постоянная закона смещения Вина. - постоянная закона смещения Вина.Искомая длина волны: 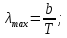 На основании второго закона Вина спектральная плотность энергетической светимости при данной температуре равна: 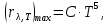 где 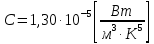 - постоянная. - постоянная.Численно: 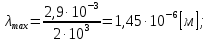 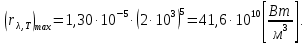 Ответ: 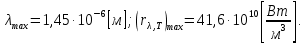 Задача№ 414 На поверхность металла падает монохроматический свет с длиной волны 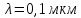 . Красная граница фотоэффекта равна . Красная граница фотоэффекта равна 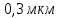 . Какая доля энергии фотона расходуется на сообщение электрону кинетической энергии ? . Какая доля энергии фотона расходуется на сообщение электрону кинетической энергии ?
работу выхода. Остаток энергии реализуется в виде кинетической энергии теперь уже свободного электрона. 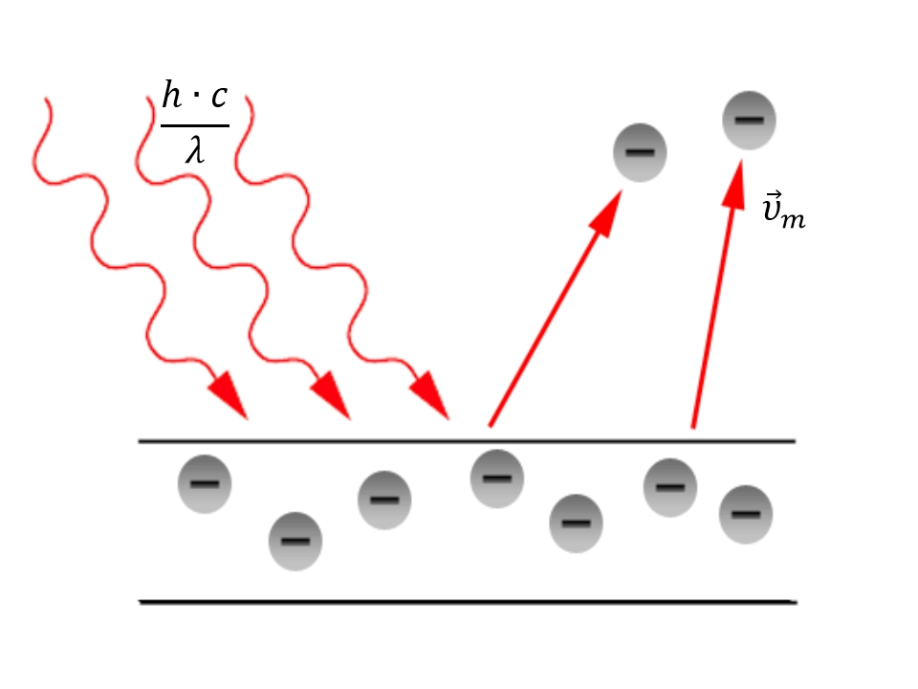 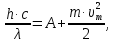 где 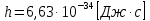 - постоянная Планка, - постоянная Планка, 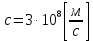 - скорость света в вакууме, - скорость света в вакууме, 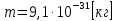 - масса электрона, - масса электрона, 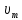 - максимальная скорость электрона. - максимальная скорость электрона.Работа выхода электрона из металла при известной красной границе равна: 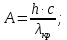 Уравнение Эйнштейна примет вид: 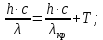 Искомое отношение равно: 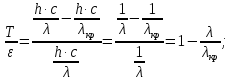 Численно: 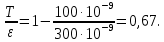 Ответ: 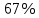 - энергии фотона пошло сообщение электрону кинетической энергии. - энергии фотона пошло сообщение электрону кинетической энергии.Задача № 429 Энергия 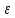 падающего фотона равна энергии покоя электрона. Сколько процентов энергии падающего фотона приходится на рассеянный фотон и сколько процентов получает электрон отдачи, если угол рассеяния падающего фотона равна энергии покоя электрона. Сколько процентов энергии падающего фотона приходится на рассеянный фотон и сколько процентов получает электрон отдачи, если угол рассеяния 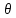 равен: равен: 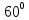 , , 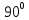 , , 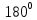 ? ?
где 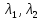 – длины волн падающего и рассеянного фотонов соответственно, – длины волн падающего и рассеянного фотонов соответственно, 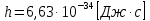 – постоянная Планка, – постоянная Планка, 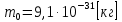 – масса электрона, – масса электрона, 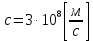 – скорость света в вакууме, – скорость света в вакууме, 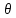 – угол рассеяния. – угол рассеяния.Преобразуем крайнюю формулу с учетом того, что: 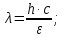 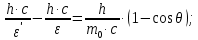 Сократим все выражение на 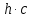 и учтем, что и учтем, что 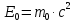 : :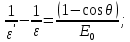 Отсюда энергия рассеянного фотона равна: 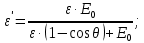 Энергия, полученная электроном отдачи, равна разности энергии падающего и рассеянного фотонов равна: 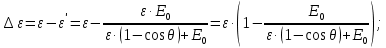 Доля этой энергии: 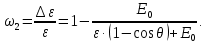 Доля энергии, которую сохранит падающий фотон: 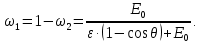 Численно: Для 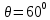 : :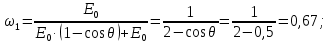 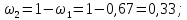 Для 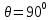 : :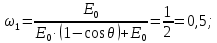 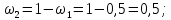 Для 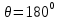 : :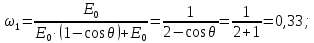 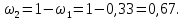 Ответ: 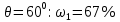 - сохранил падающий фотон, - сохранил падающий фотон, 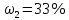 - получил электрон отдачи; - получил электрон отдачи; 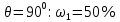 - сохранил падающий фотон, - сохранил падающий фотон, 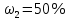 - получил электрон отдачи; - получил электрон отдачи;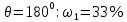 - сохранил падающий фотон, - сохранил падающий фотон, 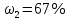 - получил электрон отдачи. - получил электрон отдачи.Задача № 430 Вычислить по теории атома Бора радиус 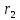 второй орбиты электрона в атоме водорода. Найти длину волны излучения, испускаемого при переходе электрона с этой орбиты на орбиту с второй орбиты электрона в атоме водорода. Найти длину волны излучения, испускаемого при переходе электрона с этой орбиты на орбиту с 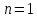 . .
где 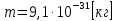 - масса электрона, - масса электрона, 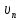 - скорость электрона на -ой орбите, - скорость электрона на -ой орбите, 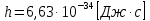 – постоянная Планка. – постоянная Планка.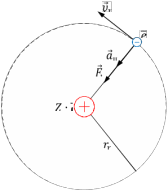 Запишем второй закон Ньютона для электрона, движущегося вокруг ядра под действием кулоновской силы притяжения ядра: 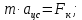 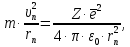 где 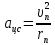 – центростремительное ускорение, – центростремительное ускорение, 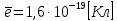 - заряд электрона, - заряд электрона, 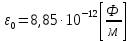 - электрическая постоянная. - электрическая постоянная.Выражая из этих двух закономерностей радиус, получим: 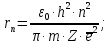 Сериальная формула, определяющая длину волны света, излучаемого атомом водорода при переходе электрона с одной орбиты на другую: 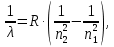 где 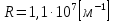 - постоянная Ридберга. - постоянная Ридберга.Искомая длина волны: 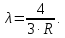 Численно: 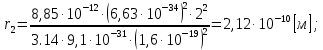 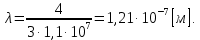 Ответ: 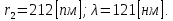 Задача № 442 Сравнить длины волн де Бройля для протона и шарика массой 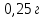 , движущихся с одинаковой скоростью. , движущихся с одинаковой скоростью.
Искомое отношение: 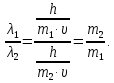 Численно: 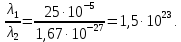 Ответ: длина волны де Бройля для протона больше длины волны де Бройля шарика при движении их с одинаковой скоростью в  раза. раза.Задача № 455 Сколько процентов начального количества актиния останется: через 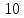 дней, через дней, через 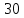 дней? ( дней? (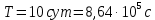 ). ).
вещества, 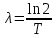 - постоянная радиоактивного распада. - постоянная радиоактивного распада. Доля нераспавшихся: 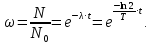 Численно: 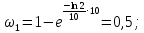 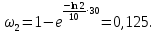 Ответ: за время 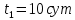 останется нераспавшимися останется нераспавшимися 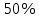 ядер актиния, за время ядер актиния, за время 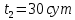 - - 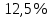 . .Задача № 468 Найти дефект массы и удельную энергию связи ядра атома 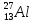 . .
где 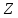 – число протонов, – число протонов, 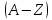 – число нейтронов, – число нейтронов, 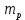 – масса протона, – масса протона, 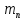 – –масса нейтрона, 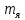 – масса ядра. – масса ядра.Массу ядра можно получить, если из массы атома вычесть массу электронов, образующих электронную оболочку атома: 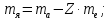 Тогда: 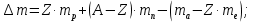 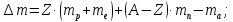 Заметим, что 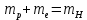 , где , где 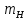 – масса атома водорода. – масса атома водорода.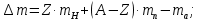 Искомый дефект массы ядра алюминия 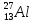 : :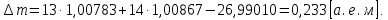 Энергия связи ядра определяется выражением: 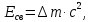 где 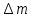 - дефект массы ядра, - дефект массы ядра, 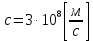 - скорость света в вакууме. - скорость света в вакууме.Если энергию выражать в мегаэлектрон-вольтах, а дефект массы получен в атомных единицах массы, то: 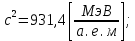 Энергия связи ядра алюминия 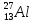 : :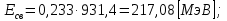 Удельная энергия связи: 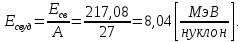 Ответ: 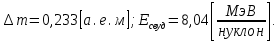 Задача № 479 Найти энергию, выделяющуюся при реакции: 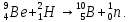
бомбардирующей частицы; 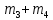 - сумма масс покоя ядер продуктов реакции. - сумма масс покоя ядер продуктов реакции.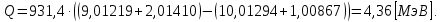 В джоулях: 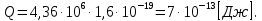 Ответ: 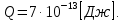 |

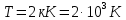
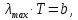
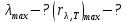
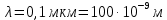
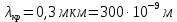
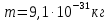
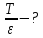
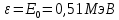
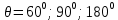
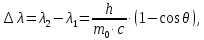
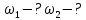
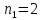
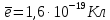
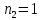
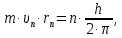
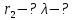
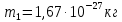
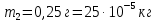
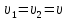
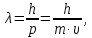
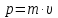 – импульс частицы.
– импульс частицы.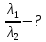
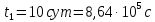
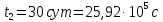
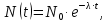
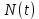 − количество еще не распавшегося
− количество еще не распавшегося 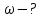
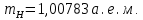
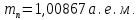
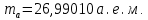
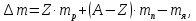
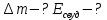
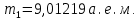
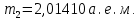
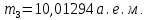
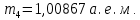
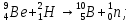
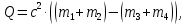
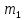 и
и 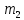 - массы покоя ядра-мишени и
- массы покоя ядра-мишени и