кр 4 геометрия векторы. 1 2) и c (1 0). Найдите
 Скачать 70.54 Kb. Скачать 70.54 Kb.
|
|
Вариант 1 1. Даны точки A (−3; 1), B (1; −2) и C (−1; 0). Найдите: 1) координаты векторов 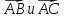 ; ; 2) модули векторов 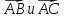 ; ; 3) координаты вектора 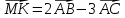 ; ; 4) скалярное произведение векторов 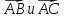 ; ; 5) косинус угла между векторами 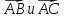 . . 2. Начертите треугольник ABC. Постройте вектор: 1) 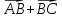 ; 2) ; 2) 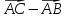 ; 3) ; 3) 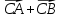 . . 3. Дано векторы  айдите вектор с= - айдите вектор с= -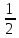 4. На стороне ВС ромба ABCD лежит точка К так, что ВК = КС, О — точка пересечения диагоналей. Выразите векторы АО, АК, KD через векторы АВ = m и AD = n. Вариант 2 1. Даны точки A (2; −1), C (3; 2) и D (−3; 1). Найдите: 1) координаты векторов 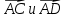 ; ; 2) модули векторов 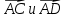 ; ; 3) координаты вектора 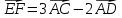 ; ; 4) скалярное произведение векторов 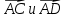 ; ; 5) косинус угла между векторами 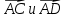 . . 2. Начертите треугольник ABC. Постройте вектор: 1) 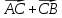 ; 2) ; 2) 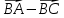 ; 3) ; 3) 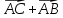 . . 3     . Дано векторы x (-1; 6) и k(5;-3). Найдите вектор t = 4,8 x- . Дано векторы x (-1; 6) и k(5;-3). Найдите вектор t = 4,8 x- 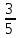 k и его модуль. k и его модуль.4.На стороне CD квадрата ABCD лежит точка Р так, что СР = PD, О – точка пересечения диагоналей. Выразите векторы ВО, ВР, РА через векторы ВА= x и ВС=y Вариант 1 1. Даны точки A (−3; 1), B (1; −2) и C (−1; 0). Найдите: 1) координаты векторов 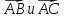 ; ; 2) модули векторов 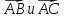 ; ; 3) координаты вектора 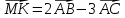 ; ; 4) скалярное произведение векторов 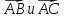 ; ; 5) косинус угла между векторами 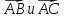 . . 2. Начертите треугольник ABC. Постройте вектор: 1) 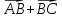 ; 2) ; 2) 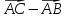 ; 3) ; 3) 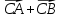 . . 3. Дано векторы 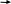 айдите вектор с= - айдите вектор с= -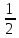 4. На стороне ВС ромба ABCD лежит точка К так, что ВК = КС, О — точка пересечения диагоналей. Выразите векторы АО, АК, KD через векторы АВ = m и AD = n.. Вариант 2 1. Даны точки A (2; −1), C (3; 2) и D (−3; 1). Найдите: 1) координаты векторов 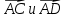 ; ; 2) модули векторов 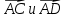 ; ; 3) координаты вектора 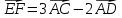 ; ; 4) скалярное произведение векторов 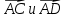 ; ; 5) косинус угла между векторами 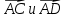 . . 2. Начертите треугольник ABC. Постройте вектор: 1) 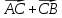 ; 2) ; 2) 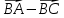 ; 3) ; 3) 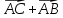 . . 3  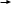   . Дано векторы x (-1; 6) и k(5;-3). Найдите вектор t = 4,8 x- . Дано векторы x (-1; 6) и k(5;-3). Найдите вектор t = 4,8 x- 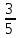 k и его модуль. k и его модуль.4.На стороне CD квадрата ABCD лежит точка Р так, что СР = PD, О – точка пересечения диагоналей. Выразите векторы ВО, ВР, РА через векторы ВА = x и ВС = y. Контрольная работа по теме «Векторы» 9 класс Вариант 3 1. Даны точки A (3; −2), B (1; −1) и C (−1; 1). Найдите: 1) координаты векторов 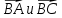 ; ; 2) модули векторов 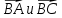 ; ; 3) координаты вектора 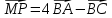 ; ; 4) скалярное произведение векторов 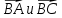 ; ; 5) косинус угла между векторами 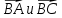 . .2. Начертите треугольник ABC. Постройте вектор: 1) 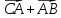 ; 2) ; 2) 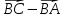 ; 3) ; 3) 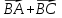 . . 3. Даны векторы 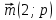 и и 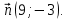 При каком значении p векторы При каком значении p векторы 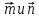 : : 1) коллинеарны; 2) перпендикулярны? 4. На сторонах AB и AD параллелограмма ABCD отмечены соответственно точки E и F так, что AE : EB = 7 : 2, AF : FD = 5 : 1. Выразите вектор 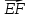 через векторы через векторы 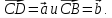 5. Найдите косинус угла между векторами 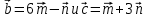 , если , если 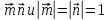 . .Вариант 4 1. Даны точки A (1; 5), B (−3; 2) и C (2; 3). Найдите: 1) координаты векторов 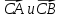 ; ; 2) модули векторов 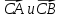 ; ; 3) координаты вектора 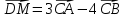 ; ; 4) скалярное произведение векторов 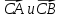 ; ; 5) косинус угла между векторами 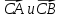 . .2. Начертите треугольник DEF. Постройте вектор: 1) 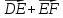 ; 2) ; 2) 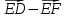 ; 3) ; 3) 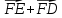 . . 3. Даны векторы 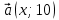 и и 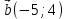 . При каком значении x векторы . При каком значении x векторы 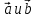 : : 1) коллинеарны; 2) перпендикулярны? 4. На сторонах AD и CD параллелограмма ABCD отмечены соответственно точки S и T так, что AS : SD = 5 : 3, CT : TD = 2 : 1. Выразите вектор 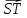 через векторы через векторы 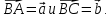 5. Найдите косинус угла между векторами 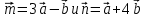 , если , если 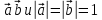 . . |
