Проектный расчет вибростенда. 1.2 Проектный расчет конструкции стенда. 1. 2 Проектный расчет конструкции стенда 1 Расчет основных параметров вибрационного стенда
 Скачать 305.96 Kb. Скачать 305.96 Kb.
|
 1.2 Проектный расчет конструкции стенда 1.2.1 Расчет основных параметров вибрационного стенда На рисунке 1.4 представлена простейшая динамическая схема вибровозбудителя. При составлении уравнений движения принято: 1) подвижная система перемещается вдоль оси вибровозбудителя; 2) масса подвесок подвижной системы незначительна; 3) механические сопротивления считаются пропорциональными первой степени скорости движения; 4) изменение индуктивности и активного сопротивления подвижной катушки в зависимости от частоты протекающего тока не учитывается; 5) магнитопровод возбудителя жестко соединен с неподвижным основанием. За исходные данные принимаем: Магнитная индукция B=0,55 [Тл]; Длина катушки h=260 [мм]; Диаметр катушки D=600 [мм]; Сила тока I=200 [А]; Виброускорение а=800 [м/с2]; Перемещение подвижной системы ∆y=20 [мм]; Масса подвижной системыm=300 [кг]. Масса объекта испытанийmоб=2000 [кг]. Виброгенератор работает по следующем принципу: движение генерируется током, проходящим через катушку, расположенную в магнитном поле. Сила, затраченная на ускорение движущегося элемента пропорциональна току возбуждения и магнитному потоку. Таким образом, контролируя ток, мы можем контролировать уровень вибрации виброгенератора. В маленьких виброгенераторах магнитное поле продуцируется постоянным магнитом, тогда как для виброгенераторов больших размеров необходимы электромагниты. Возможный уровень ускорения определяется максимальным током и нагрузкой. Однако в области низких частот уровень ускорения будет ниже из-за ограничения на смещение движущегося элемента. Верхнюю границу частоты определяет резонанс движущегося элемента. 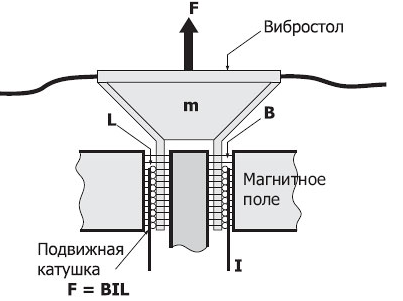 Рисунок 1.4 – Устройство виброгенератора Значение вынуждающей силы определяется по формуле: F(t)=Bli(t), F=ma (1.1) где B – магнитная индукция; l – общая длина проводника; i(t)=Isinωt – сила тока; а – виброускорение. 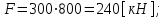 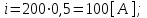 Отсюда длина проводника 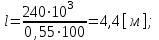 На рисунке 1.5 представлена динамическая схема вибровозбудителя, АЧХ вибростенда. 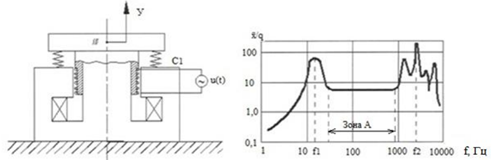 Рисунок 1.5 - Динамическая схема вибровозбудителя, АЧХ вибростенда Движение подвижной системы описывается уравнением: m 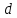 2y/dt2+bdy/dt+c1y=Bli, (1.2) 2y/dt2+bdy/dt+c1y=Bli, (1.2)где y – перемещение подвижной системы; m – масса подвижной системы; b – коэффициент сопротивления при вязком трении; c1 – коэффициент жесткости подвески. При движении в магнитном поле в проводнике индуктируется электродвижущая сила (противо-ЭДС): E=-Bl 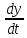 (1.3) (1.3)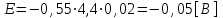 Уравнение, связывающее электрические параметры подвижной обмотки с ее движением: L 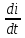 + Ri= -Bl + Ri= -Bl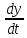 + u(t), (1.4) + u(t), (1.4)где L – индуктивность подвижной обмотки; R – активное сопротивление подвижной обмотки; u– переменное напряжение, подаваемое на подвижную обмотку. Система уравнений (1.2) и (1.4) может быть представлена в виде: (mp2+bp+cl)y=Bli; (1.5) (Lp+R)i=Blpy +U(t) (1.6) Из уравнений (1.5) и (1.6) получим: (mp2+bp+cl) (Lp+R)y=Blu(t)-B2l2py (1.7) На рисунке 1.6 показана структурная схема системы, описываемой уравнением (1.7). 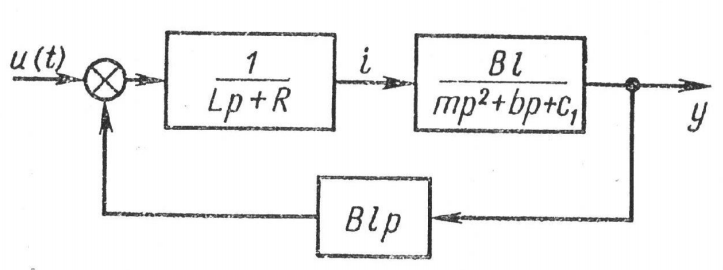 Рисунок 1.6 - Структурная схема вибровозбудителя Таким образом, простейшая динамическая модель электродинамического возбудителя колебаний представляет собой замкнутую линейную систему третьего порядка с отрицательной обратной связью по скорости. Значительная часть реальных режимов испытаний построена так, что амплитуды напряжения или силы тока не поддерживаются постоянными, а изменяются по заданному закону во всем диапазоне частот. Выбор частотного диапазона работы вибровозбудителя (без подробного рассмотрения динамики всей системы) определяется собственными частотами механической части вибровозбудителя w1и w2. Приближенная собственная частота колебаний подвижной системы (рассматриваемой как сосредоточенная масса) на подвесках: w1= 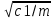 Приближенная первая собственная частота продольных колебаний подвижной системы, рассматриваемой как двухмассовая система, при c1 =0 w2= 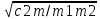 Низшая частота рабочего диапазона частот определяется значениями w>w1. При меньших частотах для получения заданных ускорений необходимо увеличить входной сигнал и, следовательно, увеличить мощность усилительного устройства сверх ее номинального значения. Достаточно низкое значение ω обеспечивается конструкцией подвески. Верхняя граница рабочего диапазона частот определяется частотой 2. Приближенный расчет ускорения, создаваемого в вибровозбудителе в диапазоне w1<w<w2может быть выполнен без полного исследования динамики системы. Если не учитывать воздействия противо-ЭДС и рассматривать уравнение (1.7), то, полагая b= 0 и c1 = 0, получим: m 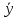 =Bli, (1.8) =Bli, (1.8)при гармоническом изменении силы тока i=sinwt, 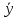 =- =-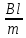 sinwt; амплитуды ускорения w и вынуждающей силы F соответственно: sinwt; амплитуды ускорения w и вынуждающей силы F соответственно:w0= 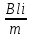 и F0=mw0 и F0=mw0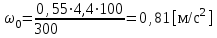 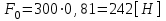 Зная особенности конструкции и назначение вибровозбудителя, можно выбрать, полную длину проводника, а значит, и размеры подвижной обмотки. При разработке конструктивного решения определяется масса m подвижной системы. При более полных расчетах вибровозбудителя осуществляют расчеты системы магнитопровода, обмотки возбуждения, системы охлаждения. Предельные возможности вибровозбудителя определяются энергетическими процессами, протекающими в нем. Уровень воспроизводимой вибрации зависит от мощности вибровозбудителя. Мгновенная мощность вибровозбудителя: N=yF=yBli, (1.9) 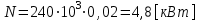 Полная мощность, потребляемая вибровоозбудителем, может быть представлена как: N=kF02/B2Dh, (1.10) где F0 – амплитуда гармонической вынуждающей силы; B – индукция в рабочем зазоре; D, h – основные размеры подвижной катушки. Коэффициент 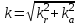 , где , где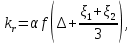 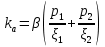 . .где f– частота изменения тока в подвижной обмотке; ∆– рабочий зазор; p1 иp2– удельные сопротивления материала; α, β- постоянные коэффициенты; ξ1 и ξ2 – глубина проникновения электромагнитной волны в материал обмотки и экранов. Коэффициент k=0,061, тогда 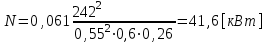 С целью исключения на рабочем месте лабораторного зала резонансных эффектов необходимо, чтобы не были близки значения следующих величин: – собственной частоты подвески стола вибратора вместе с объектом испытаний: 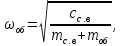 где сс.в жесткость подвески стола вибратора; mс.в,mоб – массы стола вибратора и объекта испытаний соответственно; 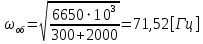 – собственной частоты фундамента со статором вибратора: 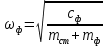 (1.11) (1.11)где cф – жесткость фундамента; mф, mсm– массы фундамента и статора фундамента соответственно; 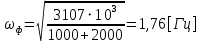 – собственной частоты wлк лабораторного корпуса. Жесткость сс.в подвески стола вибратора должна находиться в определенном диапазоне. Собственная частота wоб подвески стола вибратора зачастую получается того же порядка, что и собственная частота wл.к лабораторного зала. В этом случае необходима изоляция вибратора и лабораторного зала. Это достигается тем, что фундамент под вибратор сооружают изолированно от фундамента лабораторного зала. Фундамент вибратора должен служить виброизолятором, для чего его собственная частотам wфдолжна быть много меньше тех частот, на которых проводятся испытания: wф<<wu Выполнение этого неравенства можно достичь, как следует из соотношения (1.11), либо уменьшением жесткости cф фундамента, либо увеличением его массы. Если масса объекта испытаний больше толкающего усилия вибратора или того же порядка, то объект вывешивается на упругих подвесках. Жесткость подвесок должна быть минимальной, чтобы частота испытаний wu и превосходила собственную частоту массы стола вибратора и объекта испытаний: wu<<w∑. Здесь w∑– собственная частота колебаний стола вибратора с объектом испытаний: 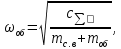 где c∑– общая жесткость подвески системы стол вибратора - объект. 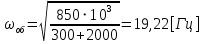 1.2.2 Расчет тока короткого замыкания Исходные данные: UФ= 220 [В] – фазное напряжение UН= 24 [В] – напряжение вторичной обмотки SН= 300 [ВА] – полная мощность вторичной обмотки S = 3 [мм2]– сечение провода l = 200 [м] – длина проводов Алюминий – материал провода rАЛ.= 0,028 [Ом мм2/м] – удельное электрическое сопротивление алюминия UК%= 5,5 % а) Рассчитывается активное сопротивление проводов: 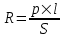 (1.12) (1.12)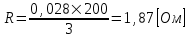 б) Индуктивное сопротивление проводов:  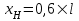 (1.13) (1.13)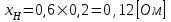 в) Определяем полное сопротивление проводов: 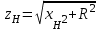 (1.14) (1.14)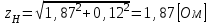 г) Рассчитывается номинальный ток во вторичной обмотке трансформатора: 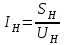 (1.15) (1.15)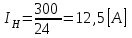 д) Рассчитывается полное сопротивление фазной обмотки трансформатора на стороне низкого напряжения: 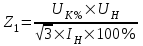 (1.16) (1.16)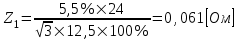 е) Ток короткого замыкания: 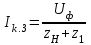 (1.17) (1.17)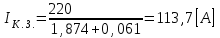 Таким образом ток КЗ составляет 113,7 А. 1.2.3 Определение положения рабочей точки транзистора –усилителя Исходные данные: КТ 819 - А – тип транзистора RК= 1 [Ом] – сопротивление коллектора R2= 200 [Ом] – сопротивление базового делителя R1= 3 [кОм] – сопротивление базового делителя EК = 8 [В] – напряжение питания На рисунке 1.7 изображена схема транзистора 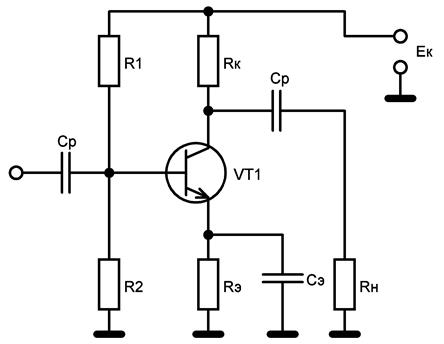 Рисунок 1.7 - Схема включения транзистора с общим эмиттером а) Напряжение смещения базы: 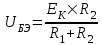 (1.18) (1.18)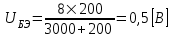 б) Определяем ток базы по входной характеристики транзистора при напряжении Uк (близкое к Ек): 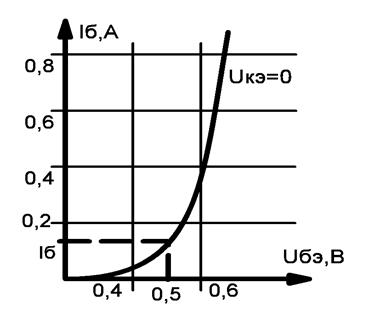 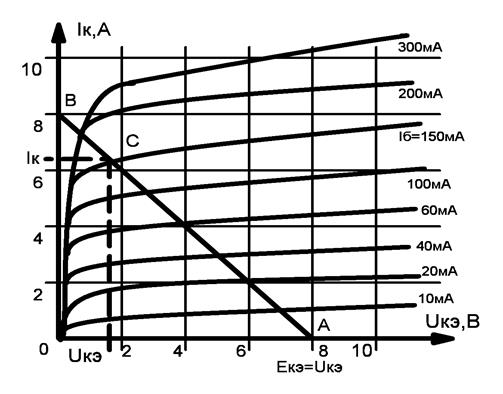 в) На выходных характеристиках транзистора определяем рабочую точку 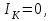 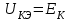 (1.19) (1.19)   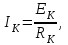 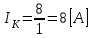 Iк = 6,3А; Uкэ = 1,8В. 1.2.4 Выбор проводов и кабелей Исходные данные: Uс= 220 [В] – напряжение сети Р = 700 [Вт] – мощность автомата Алюминий – материал провода При выборе проводов и кабелей надо учитывать условия внешней среды в месте их прокладки, напряжения, при котором они будут работать и ток нагрузки. При выборе проводов и кабелей по длительно допустимому току, его величину можно приблизительно определить по величине тока на 1 кВт мощности. Ток для двухфазного двигателя: 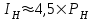 (1.20) (1.20) 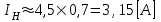 По таблице проводов, зная ток, выбираем провод: - сечение провода S = 0,5 [мм2] - марка провода А16 Соответсвенно, умелая регулировка механизмов стенда и правильная его эксплуатация предотвращают неполадки и поломки, являющиеся, зачастую, причиной длительной остановки машины, а также хороший уход и своевременный высококачественный ремонт стенда предохраняет его от преждевременного износа и будут способствовать получению точных измерений. 1.2.5 Расчет основных параметров вибрационных процессов Исходные данные: Xпик=0,01[м]; t=36000[сек]; Частота колебания: f1=5 [Гц]; f2=20 [Гц]; f3=100 [Гц]; f4=500 [Гц]; f5=2 000 [Гц]. Наиболее интенсивный и сложный вибрационный процесс имеет место в период старта ЛА и при отделении ступеней. Вибрационный процесс характеризуется высоким уровнем перегрузок и широким спектром частот (от 5 до 2000 Гц). Основными источниками вибраций в этом случае являются аэродинамические эффекты и динамическое воздействие двигательной установки. Аэродинамические эффекты проявляются в пульсации скорости ветра и пульсации давления на поверхности КА. Пульсация аэродинамического давления связана с воздействием турбулентного пограничного слоя, а также с особенностями обтекания поверхности аппарата. Динамическое воздействие двигательной установки проявляется в виде пульсации силы тяги и в виде внешнего акустического поля давления, генерируемого истекающей струей. Способность изделия противостоять разрушающему действию вибрации называется вибропрочностью, а способность сохранять свою работоспособность под действием вибрации и после её прекращения виброустойчивостью. Реальный вибрационный процесс имеет весьма сложную форму и обычно носит пространственный характер (вектор линейного виброускорения в различные моменты времени направлены не одинаково). Вибрационные процессы, искусственно создаваемые при экспериментальной отработке конструкций ЛА, существенно отличаются от реальных процессов и представляют лишь их модели. Различия состоят в том, что воспроизводимые при испытаниях вибрационные характеристики имеют, как правило, упрощенную форму и направлены вдоль фиксированной оси. В лабораторных условиях используют модели периодических и случайных вибрации. Периодической вибрацией называют процесс, в котором значение колебательной величины, характеризующий процесс (перемещение, скорость, ускорение) повторяются в той же последовательности, через равные промежутки времени Т. Наименьшие значения величины Т называют периодом колебаний. 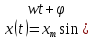 ), ),где 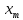 - амплитуда колебаний; - амплитуда колебаний; w=2πf - круговая частота; f-частота колебаний; φ- начальная фаза; t-время; В случае гармонических вибраций перемещенияx (t), скорость v(t) и ускорения a(t) имеют вид: Перемещения x(t): x=xпик  sin sin (2 (2 П П f f t) (1.21) t) (1.21)x1=0,01пик  sin sin (2 (2 3,14 3,14 5 5 36000)=-0,009 36000)=-0,009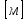 x2=0,01пик  sin sin (2 (2 3,14 3,14 20 20 36000)=0,008 36000)=0,008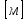 x3=0,01пик  sin sin (2 (2 3,14 3,14 100 100 36000)=-0,0076 36000)=-0,0076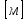 x4=0,01пик  sin sin (2 (2 3,14 3,14 500 500 36000)=0,0092 36000)=0,0092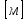 x5=0,01пик  sin sin (2 (2 3,14 3,14 2000 2000 36000)=0,0099 36000)=0,0099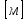 Скорость v(t): V= 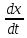 =W =W xпик xпик cos cos (w (w t) (1.22) t) (1.22)V1=30,7  (-0,009) (-0,009) cos cos (30,7 (30,7 36000)=-0,266 36000)=-0,266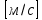 V2=122,8  0,008 0,008 cos cos (122,8 (122,8 36000)=0,452 36000)=0,452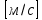 V3=614  (-0,007) (-0,007) cos cos (614 (614 36000)=2,781 36000)=2,781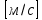 V4=3070  (0,0092) (0,0092) cos cos (3070 (3070 36000)=-10,450 36000)=-10,450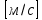 V5=12280  0,0099 0,0099 cos cos (12280 (12280 36000)=5,957 36000)=5,957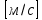 Ускорение a(t): a= 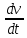 = =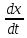 =-w2 =-w2  xпик xпик sin sin (w (w t) (1.23) t) (1.23)a1=(30,7)2  0,01 0,01 sin sin (30,7 (30,7 36000)=2,516 36000)=2,516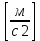 a2=(122,8)2  0,01 0,01 sin sin (122,8 (122,8 36000)=133,155 36000)=133,155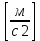 a3=(614)2  0,01 0,01 sin sin (614 (614 36000)=2872,709 36000)=2872,709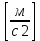 a4=(3070)2  0,01 0,01 sin sin (3070 (3070 36000)=87463,072 36000)=87463,072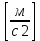 a5=(12280)2  0,01 0,01 sin sin (12280 (12280 36000)=1504968,032 36000)=1504968,032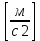 xср= 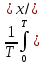 = =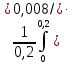 dt=5 dt=5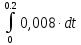 =5(0.008 =5(0.008 t t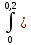 = ==5(0,008  0,2-0,008 0,2-0,008 0)= 0)=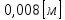 Заметим, что первая и вторая производные по времени от перемещения х(t) также изменяются по гармоническому закону с той же частотой, причем амплитуды ускорения Аm, скорости Vm и перемещения Хm связаны соотношениями: Амплитуда ускорения: 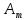 = =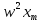 ; (1.24) ; (1.24)Амплитуда скорости: 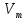 =w =w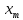 ; (1.25) ; (1.25)Первая производная опережает функцию перемещения, а вторая производная, в свою очередь, опережает первую производную на фазовый угол, равный П/2. Полигармоническая вибрация представляет собой сложный колебательный процесс, состоящий из двух или более гармонических колебаний с различными частотами. Полигармоническая вибрация может быть аналитически представлена в виде суммы более простых, гармонических вибраций. В практике виброиспытаний популярном преставлений полигармонических колебаний в виде разложения в ряд Фурье, т.е. разложение на гармонические функции : 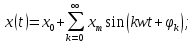 (1.26) (1.26)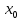 - постоянная составляющая колебательного процесса; - постоянная составляющая колебательного процесса; 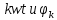 - амплитуда и начальный фазовый угол k-ый гармоник; - амплитуда и начальный фазовый угол k-ый гармоник;k- номер гармоник; w- круговая частота основной нулевой гармоник; Среднеквадратичное значение: Математическое ожидание функций, описывающее стационарный эргодический процесс, равно: mх=M 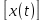 = =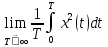 , (1.27) , (1.27)где Т-интервал наблюдения реализаций случайного процесса х(t). Элементарное представления о суммарной интенсивности любого случайного процесса дает среднее значение квадрата 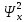 , которое представляет собой среднее из всех значений квадрата функций, описывающей процесс в пределах данной реализации. Оно определяется в виде: , которое представляет собой среднее из всех значений квадрата функций, описывающей процесс в пределах данной реализации. Оно определяется в виде: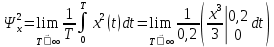 (1.28) (1.28)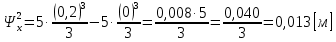 Абсолютная величина корня квадратного из среднего значения квадрата называется среднеквадратичным значением. Дисперсия характеризует степень рассеивания значений параметров случайного процесса относительно математического ожидания: 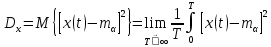 (1.29) (1.29)Математическое ожидание: 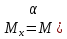 (t)]= (t)]=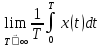 (1.30) (1.30)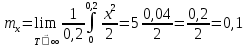 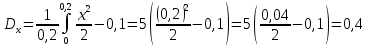 Дисперсия всегда является положительной величиной и по своему физическому смыслу представляет мощность переменных составляющих случайного процесса. Среднеквадратичные отклонения также являются характеристикой интенсивности процесса и определяется как: 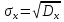 (1.31) (1.31)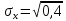 = 0,63 = 0,63Плотность распределения случайного процесса определяют вероятность того, что значение параметров процесса в произвольные моменты времени будут заключены в определенном интервале. При нормальном законе распределения она имеет вид: p(⍺)= 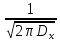 exp[ exp[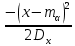 ] ]p(⍺) = 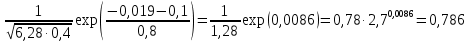 Для описания внутренней структуры случайного процесса вводят понятия автокорреляционной функции. Она характеризует степень зависимости, существующей между значениями параметров процесса в различные моменты времени. Для стационарного процесса величина автокорреляционной функции зависит не от самих моментов времени, а только от временного интервала между ними: 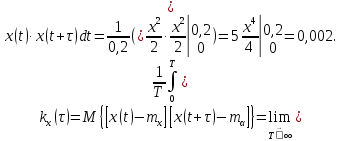 Для характеристики частотной структуры случайного процесса пользуются понятиями спектральной плотности мощности Sх(f). Для стационарного эргодического случайного процесса она выражает среднюю мощность процесса, приходящуюся на единицу полосы частот. Распределения средней мощности процесса по частоте называют спектром мощности или энергетическим спектром. Случайный процесс называют узкополосным процессом, если спектр мощности процесса сосредоточен главным образом в узкой полосе частот, и широкополосным процессом, если функция спектральной плотности вибрации. 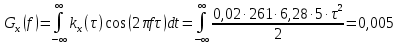 Функция односторонней спектральной плотности: 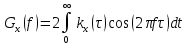 ; (1.32) ; (1.32)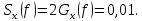 Суммарная интенсивность: 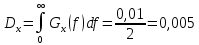 Интенсивность в диапазоне частот от 5 Гц до 2000 Гц : 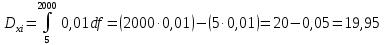 Настройка уровня вибрации изделия ведут по ускорению для полосы частот пока не будет выполнено равенство: 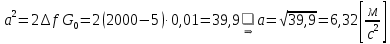 Градиент ускорения: 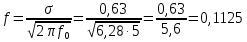 Определение собственных частот, форм колебаний и коэффициентов. Демпфирование: 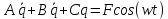 (1.33) (1.33)Используя метод многоточечного возбуждения конструкции РН в котором собственные частоты формы колебаний и коэффициент демпфирования определенным путём специального подбора возбуждаемых сил поочерёдно «чистые» собственные формы колебаний. Пологая что,Q=Fcos(wt) частота системы: 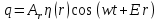 ; (1.34) ; (1.34)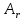 - некоторый коэффициент амплитуды колебания; - некоторый коэффициент амплитуды колебания;𝜂(r)-собственная форма колебаний; 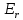 -произвольная постоянная; -произвольная постоянная;Демпфирование: F= 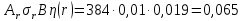 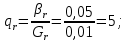 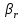 =0,05; =0,05;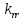 =0,03; =0,03;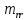 =20000; =20000;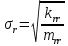 =0,01; =0,01;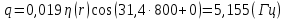 ; ;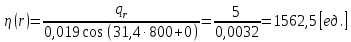 Коэффициентное демпфирование: 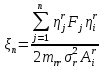 ; ;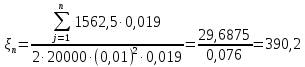 Демпфирование: 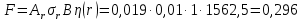 Применение стендов с электродинамическим возбуждением обосновано тем, что характеризуются весьма широким диапазоном воспроизводимых частот. При применении специального оборудования на них возможно осуществление всех основных режимов вибрационных испытаний. Стенд предназначен для работы в диапазоне 5—2000 Гц и создает амплитуду гармонической вынуждающей силы до 240 кН, и обеспечивает малый коэффициент нелинейных искажений, возможность изменения направления вибрации. |
