1. 3 Методика решения поставленной задачи

• Название: 1. 3 Методика решения поставленной задачи
• Дата: 20.10.2022
• Размер: 63.45 Kb.
• Имя файла: reshenie_zadachi.docx
• Тип: Документы; #744790

1.3 Методика решения поставленной задачи

В представленном варианте задачи дана модель распределения температуры в земной коре в виде цилиндрического куска трубопровода тепловой магистрали, защищенной изоляцией толщиной h, диаметром d, с внутренним радиусом r₁ и внешним радиусом r₂, температурой трубы T₁, которая больше, чем температура наружного воздуха T₂ (рис.1):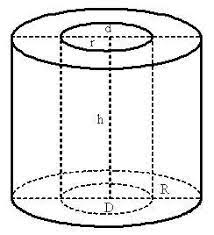



Рисунок 1 - Модель цилиндрической трубы

Целью задачи является выведение закономерности распределения температуры T на интервале .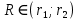

Решаем задачу в несколько этапов:

1. 
   Выводим дифференциальное уравнение.
   

Оболочка имеет форму цилиндра, а значит формула для площади его поверхности нам известна: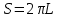

2. 
   В случае переноса тепла, не сопровождающегося переносом вещества, действует закон Фурье: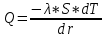
   

,

где Q=const – тепловой поток, λ – коэффициент теплопроводоности

3. 
   Переносим однотипные переменные R и Т в одну часть уравнения (причем дифференциал должен оказаться в числителе):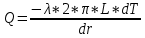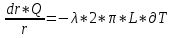
   

4. 
   Берём неопределенный интеграл от обоих частей: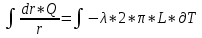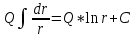
   

5. 
   Получаем итоговую формулу: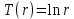
   

Графиком данной функции является гипербола, который можно построить, зная постоянные величины и, подставив данные значения r.



Теперь адаптируем задачу к сферической поверхности Земли, где:

T₁ = 800 °с – температура солидуса, T₂ = 12,1 °с - среднегодовая температура региона, R₁ = 6320 (км) – внутренний радиус, R₂ = 6370 (км) – внешний радиус.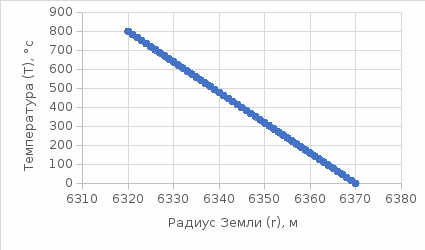