Электротехника. 05 Лекция. 1 Активный и пассивный двухполюсник
 Скачать 491 Kb. Скачать 491 Kb.
|
|
§1 4. Активный и пассивный двухполюсник. В любой ЭЦ всегда можно мысленно выделить какую-то одну ветвь, а всю остальную часть схемы, независимо от её структуры и сложности, условно изобразить некоторым прямоугольником. По отношению к выделенной ветви вся схема, обозначенная прямоугольником, представляет собой так называемый двухполюсник. 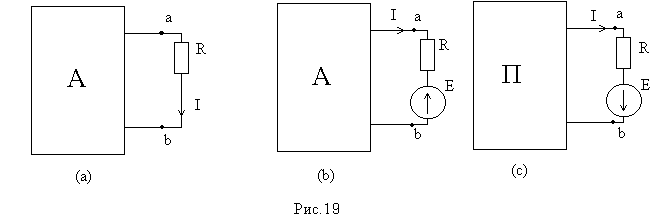 Двухполюсник – это обобщенное название схемы, которая двумя выходными зажимами (полюсами) присоединена к выделенной ветви. Если в двухполюснике есть источник ЭДС или (и) тока, то такой двухполюсник называется активным. В этом случае в прямоугольнике ставят букву А. Если в двухполюснике нет источников ЭДС и тока, то его называют пассивным. В этом случае в прямоугольнике либо не ставят никакой буквы, либо ставят букву П. §15. Передача энергии от двухполюсников нагрузке. Если нагрузка R подключена к активному двухполюснику А (рис А), то в цепи возникнет ток I и будет выделяться мощность Р: J=Uавхх/(R+Rвх); P=J2*R=(U2авхх/(R+Rвх)2)*R (1) 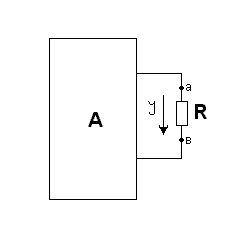 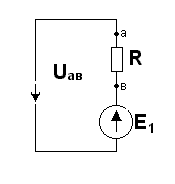 Uав ХХ в формуле (1) – напряжение холостого хода на зажимах АВ. (Это такое напряжение UавХХ=E1, которое включенное в выделенную ветвь формирует в ней ток равный нулю J1=0 т.е. по 2 закону Кирхгофа: J1R-Uав = -Е1. J1 = (Uав ХХ - Е1)/R=0 →Uав ХХ=Е1. (подробнее смотри Бессонов стр.20). Rвх в формуле (1) - входное сопротивление двухполюсника. Вспомним формулу для тока в некоторой ветви n, линейной электрической цепи, полученной с помощью метода наложения: Jn=qn1*E1+qn2*E2+…+qnn*En+…+qnm*E где q – проводимость, Е – ЭДС. і – ветви, qnn – называется входной проводимостью ветви n. R=1/qnn – входное сопротивление, q nm – называется взаимной проводимостью ветвей n и m. С другой стороны, мы можем записать: qnn=1/Rnn =Jn/Un т.е. входная проводимость любой ветви определяется отношением ЭДС. в этой ветви при равных нулю Еj=0 (j≠n) всех остальных ветвей. Другими словами, входная проводимость равна току, который потечет в ветви n, при включенном в неё ЭДС Еn =1. Определим, каково должно быть соотношение между сопротивлением на-грузки R и входным сопротивлением двухполюсника Rвх, чтобы в R выделилась максимальная мощность, чему она равна и каков при этом КПД передачи. С этой целью определим первую производную Р по R и приравниваем её к нулю: dP = (R+Rвх)2-2R(R+Rвх) = 0 (2) dR (R+Rвх)4 отсюда: R=Rвх (2а) Определив вторую производную получим, что d2P/dR2<0, т.е. мы нашли максимум функции P=f(R), подставим (2) в (1), получим: Pmax=U2авхх/4Rвх (3) Pполн= Uавхх*J= U2авхх/( Rвх +R) (4) КПД. η =P/Pполн= R/( Rвх +R) (5) Если R=Rвх, то η =0,5. Если мощность P значительная, то работать с таким низким КПД недопустимо. Для малых мощностей P (милливатт) такие схемы недопустимы. Выбор сопротивления нагрузке R, равного входному сопротивлению Rвх активного двухполюсника, называют согласованием нагрузки. Схема линии передачи показана ниже, где R1 – сопротивление линии передачи, R2 - сопротивление нагрузки, U1 – напряжение источника энергии Е в начале линии. Тогда: 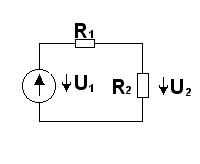 P1=U1*J P1=U1*JP2=U1*J-J2*R1 . η = P2 / P1=1-R1*J/U1= R1/R1+R2 U2= U1-R1*J Jmax=U1/R1 (R2=0) (Подробнее смотри Бессонова стр.40). Т.о. КПД тем выше, чем выше U1 – Напряжение в начале линии. На рис. ниже показано зависимость P1, P2, КПД.,U2, как функция тока по линии при неизмененном напряжении на входе линии U1 и при неизменном R1. 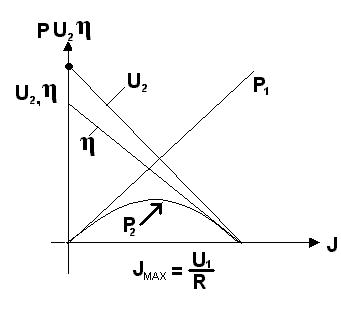 |
