Число Пи Реферат. ЧислоПи. 1. Число Пи значение, история, кто придумал

• Название: 1. Число Пи значение, история, кто придумал
• Анкор: Число Пи Реферат
• Дата: 29.08.2022
• Размер: 95.5 Kb.
• Имя файла: ЧислоПи.docx
• Тип: Документы; #655934

1. Число Пи - значение, история, кто придумал

Число Пи – математическая константа, которая выражает отношение длины окружности к её диаметру. Равна приблизительно 3,141592653589793238462643... Обозначается греческой буквой - π.

Некоторые могут подумать, раз это отношение обозначается греческой буквой, стало быть, его вывел некий греческий математик. На самом деле об этом история умалчивает. Зато имеются данные о том, кто впервые использовал в своих работах это обозначение.

Обозначение числа Пи буквой π впервые использовал английский математик (преподаватель) Уильям Джонс в 1706 году в своей работе "Synopsis Palmariorum Matheseos" (что в переводе на русский язык означает "Обозрение достижений математики"). Немного позже швейцарский математик Леонард Эйлер (1707-1783) использовал это обозначение (π) в своих работах, получивших всемирное признание. Вскоре после этого появилась тенденция к обозначению числа Пи греческой литерой π.

Все окружности похожи

Если сравнить окружности отличных друг от друга размеров, то можно заметить следующее: размеры разных окружностей пропорциональны. А это значит, что при увеличении диаметра окружности в некоторое количество раз, увеличивается и длина этой окружности в такое же количество раз. Математически это записать можно так:



где C1 и С2 – длины двух разных окружностей, а d1 и d2 – их диаметры.
Это соотношение работает при наличии коэффициента пропорциональности – уже знакомой нам константы π. Из отношения (1) можно сделать вывод: длина окружности C равна произведению диаметра этой окружности на независящий от окружности коэффициент пропорциональности π:

C = πd.

Также эту формулу можно записать в ином виде, выразив диаметр d через радиус R данной окружности:

С = 2πR.

Как раз эта формула и является проводником в мир окружностей для семиклассников.

Еще с древности люди пытались установить значение этой константы. Так, например, жители Месопотамии вычисляли площадь круга по формуле:



где S – площадь круга, C – длина окружности (круга). Если в эту формулу подставить уже знакомые школьнику выражения площади круга S = πr² и длины окружности С = 2 πR, то мы получим:



, откуда π = 3.

В древнем Египте значение для π было точнее. В 2000-1700 годах до нашей эры писец, именуемый Ахмесом, составил папирус, в котором мы находим рецепты разрешения различных практических задач. Так, например, для нахождения площади круга он использует формулу:



Из каких соображений он получил эту формулу? – Неизвестно. Вероятно, на основе своих наблюдений, впрочем, как это делали и другие древние философы.

По стопам Архимеда

Какое из двух числе больше 22/7 или 3.14 ?

-Они равны.

Почему ?

- Каждое из них равно π.

А. А. Власов. Из Экзаменационного билета.

Некоторы полагают, что дробь 22/7 и чисо π тождественно равны. Но это является заблуждением. Помимо вышеприведенного неверного ответа на экзамене (см. эпиграф) к этой группе можно также добавить одну весьма занимательную головоломку. Задание гласит: "переложите одну спичку так, чтобы равенство стало верным".



Решение будет таковым: нужно образовать "крышу" для двух вертикальных спичек слева, используя одну из вертикальных спичек в знаменателе справа. Получится визуальное изображение буквы π.

Многие знают, что приближение π = 22/7 определил древнегреческий математик Архимед. В честь этого часто такое приближение называют "Архимедовым" числом. Архимеду удалось не только установить приближенное значение для π, но также найти точность этого приближения, а именно – найти узкий числовой промежуток, которому принадлежит значение π. В одной из своих работ Архимед доказывает цепь неравенств, которая на современный лад выглядела бы так: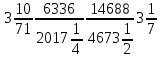



можно записать проще: 3,140 909 < π < 3,1 428 265...

Как видим из неравенств, Архимед нашел довольно-таки точное значение с точностью до 0,002. Самое удивительно то, что он нашел два первых знака после  запятой: 3,14... Именно такое значение чаще всего мы используем в несложных расчетах.

Практическое применение

Едут двое в поезде:

− Вот смотри, рельсы прямые, колеса круглые.
Откуда же стук?

− Как откуда? Колеса-то круглые, а площадь
круга пи эр квадрат, вот квадрат-то и стучит!

Как правило, знакомятся с этим удивительным числом в 6-7 классе, но более основательно им занимаются к концу 8-го класса. В этой части статьи мы приведем основные и самые важные формулы, которые пригодятся вам в решении геометрических задач, только для начала условимся принимать π за 3,14 для удобства подсчета.

Пожалуй, самая известная формула среди школьников, в которой используется π, это – формула длины и площади окружности. Первая – формула площади круга – записывается так:



где S – площадь окружности, R – ее радиус, D – диаметр окружности.

Длина окружности, или, как ее иногда называют, периметр окружности, вычисляют по формуле:

С = 2 πR = πd,

где C – длина окружности, R – радиус, d – диаметр окружности.

Понятно, что диаметр d равен двум радиусам R.

Из формулы длины окружности можно легко найти радиус окружности:



Обозначения для этих формул остаются те же.

Диаметр окружности можно найти по формуле:



где  D – диаметр, С – длина окружности, R – радиус окружности.

Это базовые формулы, знать которые должен каждый ученик. Также иногда приходится вычислять площадь не всей окружности, а только ее части – сектора. Поэтому представляем вам её – формулу для вычисления площади сектора окружности. Выглядит она так:



где S – площадь сектора, R – радиус окружности, α – центральный угол в градусах.

Такое загадочное 3,14

И правда, оно загадочно. Потому что в честь этих магических цифр устраивают праздники, снимают фильмы, проводят общественные акции, пишут стихи и многое другое.

Например, в 1998 году вышел фильм американского режиссера Даррена Аронофски под названием "Пи". Фильм получил множество наград.

Каждый год 14 марта в 1:59:26 люди, интересующиеся математикой, празднуют "День числа Пи". К празднику люди подготавливают круглый торт, усаживаются за круглый стол и обсуждают число Пи, решают задачи и головоломки, связанные с Пи.

Вниманием это удивительное число не обошли и поэты, неизвестный написал:
Надо только постараться и запомнить всё как есть – три, четырнадцать, пятнадцать, девяносто два и шесть.

Давайте развлечемся!

Вашему вниманию предлагаются интересные ребусы с числом Пи. Разгадайте слова, какие зашифрованы ниже.

1. π р

2. π ^L

3. π k

Ответы: 1. Пир; 2. Надпил; 3. Писк.

2. Как запомнить число ПИ

Наверное, чтобы превзойти его результат, нужен особый талант. Но просто удивить друзей хорошей памятью способен каждый. Главное — использовать одну из мнемонических техник, которая потом может пригодиться и для чего-нибудь еще.

Структурировать данные

Самый очевидный способ — разбить число на одинаковые блоки. Например, можно представить π как телефонную книгу с десятизначными номерами, а можно — как причудливый учебник истории (и будущего), где перечислены годы. Много так не запомнишь, но, чтобы произвести впечатление, хватит и пары десятков знаков после запятой.

Превратить число в историю

Считается, что самый удобный способ запомнить цифры — придумать историю, где им будет соответствовать количество букв в словах (ноль было бы логично заменить пробелом, но тогда большинство слов сольется; вместо этого лучше использовать слова из десяти букв). По этому принципу построена фраза "Можно мне большую упаковку кофейных зерен?" на английском языке:[]

May — 3,

I — 1

have — 4

a — 1

large — 5

container — 9

of — 2

coffee — 6

beans — 5

В дореволюционной России придумали похожее предложение: "Кто и шутя и скоро пожелает(ъ) Пи узнать число, уже знает(ъ)". Точность — до десятого знака после запятой: 3,1415926536. Но проще запомнить более современный вариант: "Она и была, и будет уважаемая на работе". Есть и стихотворение: "Это я знаю и помню прекрасно — пи, многие знаки мне лишни, напрасны". А советский математик Яков Перельман сочинил целый мнемонический диалог:

— Что я знаю о кругах? (3,1415)

— Вот и знаю я число, именуемое пи — молодец! (3,1415927)

— Учи и знай в числе известном за цифрой цифру, как удачу примечать! (3,14159265359)

Американский математик Майкл Кит и вовсе написал целую книгу Not A Wake, в тексте которой содержится информация о первых 10 тыс. цифр числа π.

Заменить цифры буквами

Кому-то легче запомнить бессвязные буквы, чем случайные цифры. В этом случае цифры заменяются первыми буквами алфавита. Первое слово в названии рассказа Cadaeic Cadenza Майкла Кита появилось именно таким образом. Всего в этом произведении закодировано 3835 знаков числа пи — правда, тем же способом, что в книге Not a Wake.

В русском языке для подобных целей можно использовать буквы от А до И (последняя будет соответствовать нолю). Насколько удобно будет запоминать составленные из них комбинации — вопрос открытый.

Придумать образы для комбинаций цифр

Чтобы добиться по-настоящему выдающихся результатов, предыдущие методы не годятся. Рекордсмены используют технику визуализации: изображения запомнить легче, чем цифры. Сначала нужно сопоставить каждую цифру с согласной буквой. Получится, что каждому двухзначному числу (от 00 до 99) соответствует двухбуквенное сочетание.

Допустим, один — это "н", четыре — "р", пять — "т". Тогда число 14 — это "нр", а 15 — "нт". Теперь эти пары следует дополнить другими буквами, чтобы получилось слова, например, "нора" и "нить". Всего понадобится сто слов — вроде бы много, но за ними стоят всего десять букв, поэтому запомнить не так уж сложно.

Число π предстанет в уме как последовательность образов: три целых, нора, нить и т.п. Чтобы лучше запомнить эту последовательность, изображения можно нарисовать или распечатать на принтере и поставить перед глазами. Некоторые люди просто раскладывают соответствующие предметы по комнате и вспоминают числа, разглядывая интерьер. Регулярные тренировки по этому методу позволят запомнить сотни и даже тысячи знаков после запятой — или любую другую информацию, ведь визуализировать можно не только числа.[1]

Литература

1. 
   3,14 способа запомнить число пи с большой точностью [Электронный ресурс] URL: https://tass.ru/obschestvo/4090349
   
2. 
   Мнемоника. Википедия [Электронный ресурс] URL: https://ru.wikipedia.org/wiki/мнемоника