1.Два рода электрических зарядов и их свойства. Наименьший неделимый электрический заряд. Закон сохранения электрических зарядов. Закон Кулона. Единица заряда. Электростатическое поле. Способ обнаружения поля. Напряженность как характеристика электростатического поля. Вектор напряженности, его направление. Напряженность электрического поля точечного заряда. Единицы напряженности. Принцип суперпозиции полей.
Электрический заряд- величина инвариантная, т.е. не зависит от системы отсчета, а потому не зависит от того, движется заряд или он покоится.
два рода (типа) эл.зарядов : заряды положительные и заряды отрицательные.
Экспериментально установили, что одноименные заряды отталкиваются, а разноименные притягиваются.
Электрически нейтральное тело должно иметь равное количество положительных и отрицательных зарядов, но и их распределение по объему тела должно быть равномерным.
Закон сохранения электрического заряда: алгебраическая сумма электрических зарядов любой замкнутой системы (системы не обменивающейся зарядами с внешними тепами) остается неизменной, какие бы процессы не происходили внутри этой системы.
Электрические заряды самопроизвольно не создаются и не возникают, они лишь могут разделяться и передаваться от одного тела к другому.
Существует наименьший заряд, его назвали элементарным зарядом - это заряд, который имеет электрон и заряд на теле кратен этому элементарному заряду : е=1,6*10-19 Кл. Отрицательный элементарный заряд связан с электроном, а положительный- с позитроном, у которого заряд и масса количественно совпадают с зарядом и массой электрона. Однако из-за того, что время жизни позитрона мало, на телах они отсутствуют и поэтому положительную или отрицательную заряженность тел объясняют или недостатком или избытком электронов на телах.
Закон Кулона: силы взаимодействия двух точечных зарядов, находящихся в однородной и изотропной среде, прямо пропорциональны произведению этих зарядов и обратно пропорциональны квадрату расстояния между ними, равны между собой и направлены по прямой, проходящей через эти заряды. 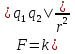 г- расстояние между зарядами q1 и q2, k-коэффициент пропорциональности, зависящий от выбора системы физических единиц. г- расстояние между зарядами q1 и q2, k-коэффициент пропорциональности, зависящий от выбора системы физических единиц.
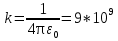 м/Ф, а м/Ф, а 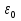 =8,85*10-12 Ф/м - диэлектрическая постоянная =8,85*10-12 Ф/м - диэлектрическая постоянная
Под точечным зарядом следует понимать заряды, сосредоточенные на телах, линейные размеры которых малы по сравнению с расстояниями между ними.
При этом заряд измеряется в кулонах - количество электричества, протекающее через поперечное сечение проводника в одну секунду при токе в 1 ампер.
Сила F направлена вдоль прямой, соединяющей заряды, т.е. является центральной силой и соответствующей притяжению (F<0) в случае разноименных зарядов и отталкиванию (F>0) в случае одноименных зарядов. Эту силу называют кулоновская сила.
Позднейшие исследования Фарадея показали, что электрическое взаимодействие между заряженными телами зависят от свойств среды, в которой происходят эти взаимодействия.
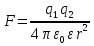
|
Если в различные точки пространства, окружающего заряженное тело, помещать другой электрический заряд, то обнаруживается, что в любой точке этого пространства на заряд действует электрическая сила. Таким образом пространство вокруг заряженного тела приобретает новое свойство: в каждой его точке можно обнаружить действие на пробный заряд электрической силы. В таких случаях говорят, что существует электрическое поле. Если заряженные тела неподвижны, то поле электростатическое.
Для того чтобы обнаружить электрическое поле нужен второй заряд. Однако само поле будет существовать независимо от этого второго пробного заряда. Электрическое поле есть та область пространства, в котором передаются взаимодействия между зарядами, находящимися на расстоянии друг от друга. В дальнейшем было доказано, что поле существующее вокруг неподвижных электрических зарядов является частным случаем более общего по своей природе электромагнитного поля. Электромагнитное поле и его частный случай электростатическое поле являются особой формой существования материи.
Для исследования свойств поля используется пробный точечный единичный положительный заряд. Помещая его в различные точки электрического поля обнаруживается, что силы, действующие на этот заряд различны.
Однако, если в одну и туже точку поля помещать различные по величине заряды, то отношение силы, действующей на заряд, к величине этого заряда остается постоянной и поэтому это отношение может быть использовано в качестве характеристики точек электрического поля. Эту величину назвали напряженность электрического поля: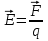
Если заряд равен единице (1 Кл) и он положительный, то Напряженность электрического поля численно равна силе, действующей на единичный положительный заряд, помешенный в данную точку поля, и имеет направление этой силы. Таким образом напряженность электрического поля есть силовая характеристика и является величиной векторной.
Направление вектора Е совпадает с направлением силы, действующей на положительный заряд. Если
поле создается положительным зарядом, то вектор Е направлен вдоль радиус-вектора от заряда во внешнее пространство (отталкивание пробной) положительного заряда); если поле создается отрицательным зарядом, то вектор Е направлен к заряду. 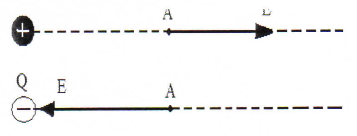
Если поле возникает от совокупного действия многих точечных зарядов, то в данном случае используется известный принцип суперпозиции : каждое из полей действует на заряд в данной точке независимо от других полей, результирующий вектор напряженности равен геометрической сумме векторов:
За единицу напряженности в системе СИ принята напряженность, при которой на единичный заряд в 1 Кл действует единичная сила в 1 Н. Эта единица имеет размерность 1В/м.
напряженности поля точечного заряда:
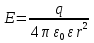
|
2.Графическое изображение эл. полей. Силовые линии поля. Однородное эл.поле. Поток вектора напряженности для однородного(и неоднородного) эл.поля. Единица потока.
Для наглядного изображения распределения векторов напряженностей Фарадей предложил проводить через каждую точку поля линию, касательная к которой совпадает с направлением вектора напряженности в данной точке. Такая линия называется силовой линией или линией напряженности. Силовым линиям приписывается следующее направление: силовые линии берут начало на положительных зарядах и заканчиваются на отрицательных зарядах. Направление вектора напряженности в данной точке силовой линии определяется следующим образом: в данную точку мысленно помещается положительный заряд и определяется направление действия электрической силы со стороны заряда, создающего поле; вектор напряженности совпадает по направлению с вектором силы.
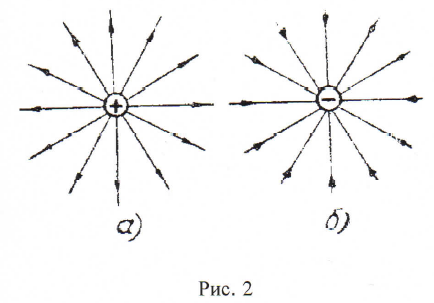 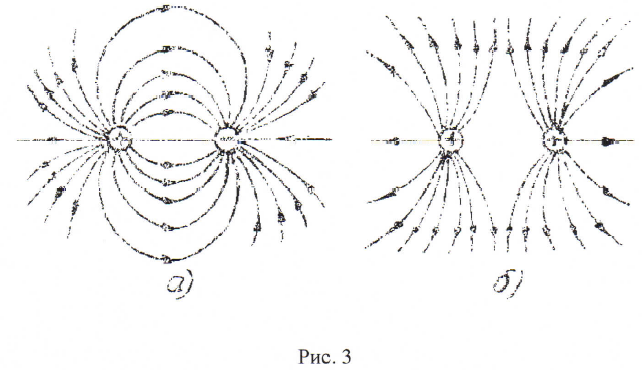
На рис.2 показаны силовые линии полей одного точечного заряда: положительного а) и отрицательного б) и на рис.3 поля двух зарядов: разноименных а) и одноименных б).
Число линий напряженности, пронизывающих единицу площади поверхности, расположенную перпендикулярно к линиям, было пропорционально величине напряженности электрического поля в данном месте.
Поле, во всех точках которого вектор напряженности имеет одно и то же значение и одно и то лее направление, называется однородным.
Общее число силовых линий, пронизывающих некоторую элементарную плоскую площадку площадью dS(рис.4) называют поток вектора напряженности.
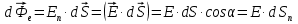
Поток вектора напряженности равен скалярному произведению вектора напряженности и вектора площади поверхности. 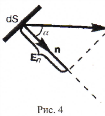
Для произвольной замкнутой поверхности поток вектора напряженности выражается через интеграл по этой замкнутой поверхности: 
Поток вектора напряженности является алгебраической величиной: он зависит не только от значения напряженности, но и от выбора направления нормали. Для замкнутых поверхностей за положительную нормаль принимается внешняя нормаль- нормаль направленная наружу от поверхности, охватывающей данную область
пространства.
|
3.Теорема Гаусса. Применение теоремыГ.
Рассматриваемое заряженное тело окружают замкнутой поверхностью и рассматривают поток через эту поверхность, то полный поток вектора напряженности электрического поля сквозь любую замкнутую поверхность равен алгебраической сумме зарядов, находящихся внутри этой поверхности и зависит от среды, окружающей заряды.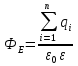
Применение теоремы Гаусса для расчета электрических поле:
1.Поле заряженной сферы.
Рассмотрим поле, создаваемое зарядами, которые находятся на поверхности полой сферы радиусом R.
Т.к. внутри этой поверхности зарядов нет, то и поток вектора напряженности через эту поверхность равен нулю, а т.к. поток выражается через напряженность и площадь поверхности (ФЕ=ЕS), то и напряженность поля тоже будет равна нулю - внутри заряженной полой сферы электрическое поле отсутствует.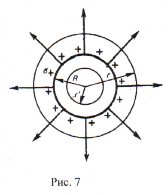
Теперь рассмотрим точку пространства, расположенную за пределами заряженной сферы (г>R).
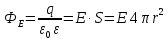 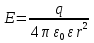
4.Работа сил эл.поля при перемещении заряда в поле. Потенциальность эл.поля. Циркуляция вектора напряженности.
 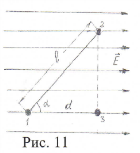
Величина работы не зависит от формы и длины пути и это свойство справедливо для любых электростатических полей. Как известно такие поля называются потенциальными или консервативными.
При перемещении заряда по любому замкнутому пути работа в электростати-ческом поле равна нулю или в более общем виде для любого замкнутого контура циркуляция вектора напряженности по контуру равна нулю: 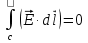
Это утверждение выражает теорему о циркуляции, при помощи которой можно дать другое определение потенциальности поля: векторное поле Е называется потенциальным, если циркуляция вектора напряжен-ности по любому замкнутому контуру равна нулю.
|
2. Поле равномерно заряженной бесконечной плоскости.
Рассмотрим плоскую бесконечную поверхность, на которой равномерно распределены заряды с поверхностной плотностью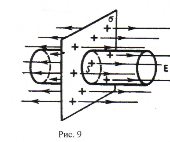
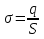 ,Кл/м2. ,Кл/м2.
Силовые линии прямые, перпендикулярные плоскости.
Общий поток вектора напряженности равен сумме потоков, пронизывающих два основания и боковую поверхность. Поток через боковую поверхность цилиндра равен нулю, т.к. силовые линии скользят вдоль поверхности (проекция вектора напряженности на нормаль к боковой поверхности равна нулю).
Таким образом, поток связан только с силовыми линиями, пронизывающими два основания.
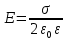
Поле бесконечной заряженной равномерно плоскости однородно, напряженность поля не зависит от расстояния от плоскости. Необходимо отметить, что реальную плоскость можно считать бесконечной, если расстояние от рассматриваемой точки до плоскости будет много меньше размеров плоскости.
5.Работа перемещения точечного заряда в поле точечного заряда (вывод). Потенциал как энергетическая характеристика эл.поля, единица измерения. Разность потенциалов. Потенциал точечного заряда; системы точечных зарядов.
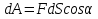 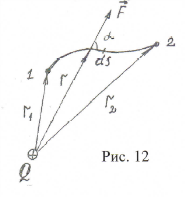
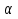 -угол между направлением силы и траекторией. -угол между направлением силы и траекторией.
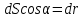
 -изменение радиус-вектора при перемещении из начала в конец участка. -изменение радиус-вектора при перемещении из начала в конец участка.
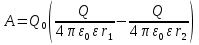
Величины, стоящие в скобках изменяются только при изменении расстояния между точкой поля и зарядом и поэтому можно ввести новую характеристику поля , которую называют потенциалом и обозначают 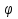 . Т. к. для точечного заряда . Т. к. для точечного заряда 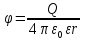
и таким образом работа перемещения заряда из т.1 в т. 2 принимает вид:
|
3. Электростатическое поле создаваемое двумя бесконечными заряженными плоскостями.
В общем случае поверхностные плотности зарядов на плоскостях могут быть разные и по величине и по знаку заряда. В этом случае для нахождения результирующего поля используется принцип суперпозиции полей (напр-яженности складываются векторно).Особый интерес представляет случай, когда повер-хностные плотности на пластинах одинаковы, но противоположны по знаку. Тогда напряженность поля вне поверхностей равна нулю, а между поверхностями: 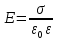 4. Поле равномерно заряженного длинного цилиндра и прямой заряженной нити. 4. Поле равномерно заряженного длинного цилиндра и прямой заряженной нити.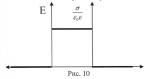
Представим что имеется бесконечно длинный цилиндр радиусом R, на котором находится равномерно
Распределенный заряд с линейной плотностью заряда 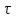 : : 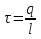 -заряд на единице длины цилиндра, Кл/м. -заряд на единице длины цилиндра, Кл/м.
В этом случае линии напряженности будут перпенди-кулярны к поверхности цилиндра. Применяя теорему Гаусса получаем формулу для г>R: 
Если г
нить это цилиндр при R → 0 .
Если конечная точка находится в бесконечности, то ее потенциал равен нулю и тогда можно дать
следующее определение потенциала:потенциалом электростатического поля в точке называется физическая величина, измеряемая работой сил поля 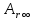 по перемещению единичного положительного заряда из данной точки в бесконечность. по перемещению единичного положительного заряда из данной точки в бесконечность.
Поскольку электростатическое поле потенциально, то потенциал измеряется потенциальной электрической энергией, приходящейся на единичный положительный заряд, помещенный в данную точку поля
Разностью потенциалов(ϕ1 –ϕ2) между точками 1 и 2 называется работа, совершаемая при
перемещении единичного положительного заряда по произвольному пути из точки 1 в точку 2.
В системе СИ единицей потенциала является вольт. 1Волът= 1Дж/Кл
|
7.Связь между напряженностью и потенциалом в общем случае и для однородных полей. Градиент потенциала.
Отношение 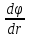 показывает изменение потенциала на единицу длины силовой линии и носит название градиента потенциала. показывает изменение потенциала на единицу длины силовой линии и носит название градиента потенциала.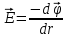 = - grad = - grad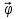
Градиент потенциала есть вектор, направленный по нормали к поверхности. Знак минус показывает, что вектор напряженности направлен в противоположную сторону от вектора градиента, то есть в сторону падения потенциала, а градиент потенциала в сторону макси-мального возрастания. На практике для вычисления напряженности поля в некоторой точке находят разность потенциалов между двумя эквипотенциальными поверх-ностями по обе стороны от точки, измеряют кратчайшее расстояние между ними(проходящее через эту точку по нормали!) и, поделив одно на другое, находят среднее значение напряженности.
|
6.Эквипотенциальные поверхности. Их расположение относительно линий напряженности.
Кроме метода изображения электрических полей при помощи силовых линий существует еще один способ наглядного графического изображения электрического поля. Для этого соединяют все точки в пространстве, имеющие одинаковые потенциалы. Тогда получают поверхность равного потенциала или эквипотенциаль-ную поверхность.
Существенной особенностью является взаимная ортогональность силовых линий и эквипотенциальных поверхностей. Действительно, т. к. на эквипотенциальной поверхность ϕ=const, то ∆ϕ =0 и тогда и работа перемеще-ния заряда по поверхности равна нулю. С другой стороны 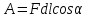 , а α=90. , а α=90. 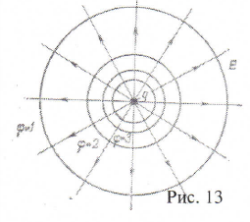
Эквипотенциальные поверхности обычно строят так, чтобы при переходе от одной поверхности к другой потенциал изменялся на одну и ту же величину, как это изображено на рис.13 для поля точечного заряда.
|
В местах, где эквипотенциальные поверхности подходят наиболее близко друг к другу, там напряженность поля будет больше. Взаимная ортогональность позволяет детализировать картину электростатического поля: по картине силовых линий можно построить эквипотенциальные поверхности и наоборот.
Установим связь между напряженностью поля и потенциалом. Для этого подсчитаем элементарную работу, совершаемую силами поля при перемещении положительного заряда Q с одной эквипотенциальной поверхности на другую (рис.14). Будем считать, что поверхности расположены на таком малом расстоянии dr по нормали к поверхностям , так что силу, действующую на перемещаемый заряд, можно считать постоянной. Тогда можно записать работу в двух формах: 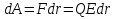 и и 
Сравнивая формулы получаем:
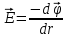 , то есть проекция вектора напряженности на некоторое направление равна производной от потенциала по этому направлению, взятой с обратным знаком. , то есть проекция вектора напряженности на некоторое направление равна производной от потенциала по этому направлению, взятой с обратным знаком.
|
10.Потенциалы поля заряженной нити (цилиндра).
Т.к. 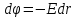 , то , то  . Эквипотенциальные поверхности будут представлять собой поверхности цилиндра радиусами г. . Эквипотенциальные поверхности будут представлять собой поверхности цилиндра радиусами г.
Тогда для разности потенциалов двух точек поля, отстоящих от нити на расстоянии r1 и r2 (r2›r1), будем иметь 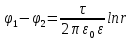
|
12.Диэлектрики в эл.поле. Молекулы полярных и неполярных диэлектриков в эл.поле. Поляризация диэлектриков. Виды поляризации.
1. Полярные диэлектрики.
В отсутствии поля каждый из диполей обладает электрическим моментом, но вектора электрических моментов молекул расположены в пространстве хаотично и сумма проекций электрических моментов на любое направление равна нулю: 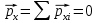
Если теперь диэлектрик поместить в электрическое поле (рис. 18), то на каждый диполь начнет действовать пара сил, которая создаст момент под действием которого диполь будет поворачиваться вокруг оси, перпендикулярной плечу, стремясь к конечному положению, когда вектор электрического момента будет параллелен вектору напряженности электрического поля. Последнему будет мешать тепловое движение молекул, внутреннее трение и т.д. и поэтому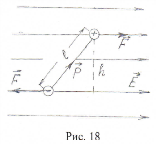
электрические моменты диполей будут составлять некоторые углы с направлением вектора внешнего поля, но теперь уже у большего числа молекул будут составляющие проекции электрических моментов на направление, совпадающее, например, с напряженностью поля и сумма проекций всех электрических моментов уже будет отлична от нуля.
Величина, показывающая способность диэлектрика созда-вать большую или меньшую поляризацию, то есть харак-теризующая податливость диэлектрика к поляризации называется диэлектрической восприимчивостью или поляризуемостью диэлектрика (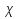 ). ). 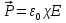
16.Поток вектора эл.индукции(однородного и неоднород-ного опля). Поток через замкнутую поверхность. Т.Гаусса для эл. Поля в среде.
Подобно потоку вектора напряженности можно ввести и понятие потока вектора индукции, оставив то же свойство, что и для напряженности-вектор индукции пропорционален числу линий, проходящих через единицу площади поверхности. Можно указать следующие свойства:
1.Поток через плоскую поверхность в однородном поле (рис. 22).В этом случае вектор индукции направлен по полю и поток линии индукции может быть выражен следующим образом:  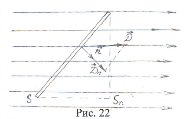
2. Поток вектора индукции через поверхность в неоднородном поле подсчитывают путем разбиения поверхности на элементы столь малые, чтобы их можно было считать плоскими, а поле вблизи каждого элемента однородным. Полный поток вектора индукции будет равен: 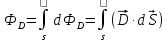
3. Поток вектора индукции через замкнутую поверхность.
Рассмотрим поток вектора индукции пересекающего замкнутую поверхность (рис.23). Условимся направление внешних нормалей считать положительными. Тогда в тех точках поверхности, где вектор индукции направлен по касательной к линии индукции наружу, угол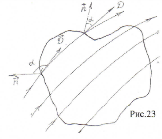
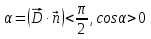 и поток линий индукции будет положительным, а там, где вектор D индукции будет положительным, а там, где вектор D направлен внутрь поверхности, поток линий индукции будет отрицательным, т.к и поток линий индукции будет положительным, а там, где вектор D индукции будет положительным, а там, где вектор D направлен внутрь поверхности, поток линий индукции будет отрицательным, т.к 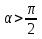 и и 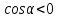 .Таким образом общий поток линий индукции пронизывающих замкнутую поверхность насквозь равен нулю. .Таким образом общий поток линий индукции пронизывающих замкнутую поверхность насквозь равен нулю.
На основании теоремы Гаусса получаем, что внутри замкнутой поверхности, проведенной в проводнике, некомпенсированные электрические заряды отсутствуют. Это свойство сохраняется и в том случае, когда проводнику сообщен избыточный заряд
На противоположной стороне возникнет равный по величине, но положительный заряд. В результате внутри проводника возникнет индуцированное электрическое поле Еинд, направленное навстречу внешнему полю, которое будет расти до тех пор, пока оно не сравняется с внешним полем и таким образом результирующее поле внутри проводника становится равно нулю. Этот процесс происходит в течение очень короткого времени.
Индуцированные заряды располагаются на поверхности проводника в очень тонком слое.
Потенциал во всех точках проводника остается одинаков, т.е. внешняя поверхность проводника является эквипотенциальной.
Замкнутый полый проводник экранирует только поле внешних зарядов. Если электрические заряды находятся внутри полости, то индукционные заряды возникнут не только на внешней поверхности проводника, но и на внутренней и замкнутая проводящая полость уже не экранирует поле электрических зарядов помещенных внутрь ее.
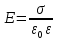 . Напряженность поля вблизи проводника прямо пропорциональна поверхностной плотности заряда на нем. . Напряженность поля вблизи проводника прямо пропорциональна поверхностной плотности заряда на нем.
|
8.Потенциал заряженной полой сферы
Так как напряженность вне сферы изменяется так же, как и для точечного заряда, то и потенциал при г>R будет выражаться как для точечного заряда. Для точек внутри полой сферы Е=0 и т.к.
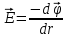 , а dϕ=0,то ϕ=const потенциал на поверхности сферы и внутри ее одинаков, а за ее пределами меняется обратно пропорционально расстоянию. Эквипотенциальные поверхности- поверхности сфер. , а dϕ=0,то ϕ=const потенциал на поверхности сферы и внутри ее одинаков, а за ее пределами меняется обратно пропорционально расстоянию. Эквипотенциальные поверхности- поверхности сфер.
На поверхности сферы и внутри ее: 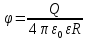 . За ее пределами (r›R): . За ее пределами (r›R): 
|
9.Потенциал поля между двумя разноименными заряженными плоскостями. Разность потенциалов.
Рассмотрим поле между пластинами, которое однородно и напряженность определяется формулой  . Возьмем точку В(рис.16), в которой потенциал будет ϕ(x), справа от положительной пластины с потенциалом ϕ1 на расстоянии х от нее. Перенесем заряд +Q с левой пластины в точку В. Работа по перемещению заряда: . Возьмем точку В(рис.16), в которой потенциал будет ϕ(x), справа от положительной пластины с потенциалом ϕ1 на расстоянии х от нее. Перенесем заряд +Q с левой пластины в точку В. Работа по перемещению заряда:  и и 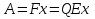 . Отсюда . Отсюда 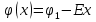 . При x=d, где d-расстояние между пластинами, имеем . При x=d, где d-расстояние между пластинами, имеем 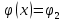 и и 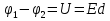 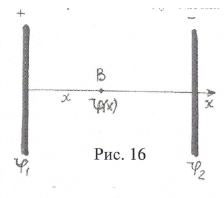
Эквипотенциальные поверхности - плоскости параллельные пластинам.
совпадают- это так называемые неполярные молекулы (молекулы кислорода, азота, парафин, бензол); в диэлектриках с кристаллической структурой, в узлах решеток которых находятся разноименные, но равные по величине ионы (МаСl,КСl);
во-вторых, имеются диэлектрики, у которых в молекулах центр положительного и отрицательного зарядов не совпадают, а находятся на некотором расстоянии друг от друга (молекулы называются полярными). Такая система из двух разноименных, но равных зарядов называется диполь, центр масс которой находится посередине и относительно его система может поворачиваться под действием пары электрических сил, действующих на заряды. Величина, характеризующая эту способность, называется электрическим моментом диполя:
Электрический момент диполя рассматривается как вектор, направленный от отрицательного заряда к положительному. 
К диэлектрикам такого типа относятся вода, хлористый водород, аммиак, ацетон. Полярные молекулы в диэлектрике несмотря на свою нейтральность могут взаимодействовать с другими молекулами, притягиваясь (или отталкиваясь) разноименными полюсами стремясь установится таким образом, чтобы потенциальная энергия системы была минимальной. Неполярные молекулы друг с другом электрически не взаимодействуют.
13.Поляризованность(вектор поляризации). Связь вектора поляризации с поверхностной плотностью связанных зарядов. Диэлектрическая восприим-чивость, относительная д.восприимчивость.
Для характеристики пространственного разделения зарядов в диэлектрике вводится понятие вектора поляризации. Вектор поляризации Р- физическая величина, численно равная электрическому моменту, которым обладает единица объема диэлектрика: 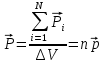 . Как вектор, он направлен так же как и вектор электрического момента, то есть по полю. . Как вектор, он направлен так же как и вектор электрического момента, то есть по полю.
Поляризованный диэлектрик можно представить как некоторый большой диполь с плечом L, на противоположных концах которого распределены некомпенсированные поляризационные заряды
противоположного знака с поверхностной плотностью  . В результате оказывается, что вектор поляризации численно равен поверхностной плотности поляризационных зарядов (при условии , что вектор поляризации перпендикулярен торцам диэлектрика). . В результате оказывается, что вектор поляризации численно равен поверхностной плотности поляризационных зарядов (при условии , что вектор поляризации перпендикулярен торцам диэлектрика).
 . В общем случае вектор поляризации в отсутствии электрического поля в различных частях диэлектрика может быть как равным нулю (для неполярных молекул)., так и отличным от нуля (для полярных). . В общем случае вектор поляризации в отсутствии электрического поля в различных частях диэлектрика может быть как равным нулю (для неполярных молекул)., так и отличным от нуля (для полярных).
|
11.Классификация веществ по эл.свойствам. Полярные и неполярные молекулы. Молекулы диэлектрика какэл.диполи. Плечо диполя. Эл.момент диполя.
Электрические заряды в веществе присутствуют в двух видах: свободные заряды и связанные заряды.
Свободными наз. заряды, которые могут перемещаться под действием сколь угодно слабого электрического поля в объеме этого вещества.
Связанными наз. заряды, которые под действием даже сильных электрических полей ,(но слабее так называемых атомных полей порядка 10 В/м) очень незначительно смещаются около положения равновесия.
В зависимости от наличия тех или иных зарядов в веществе, разные по природе вещества проводят электрический ток по-разному: вещества первого рода-проводники имеют свободные заряды с концентрацией порядка 1022—1024см-3 ; в веществах второго рода- в диэлектриках присутствуют в основном связанные заряды (хотя и имеется некоторая концентрация свободных зарядов, но значительно меньше, чем в проводниках -порядка 108-1010 см-3); особое место занимают полупроводники- концентрация свободных зарядов меняется от 1012 до 1015 см-3.
В диэлектриках существуют связанные заряды, общий электрический заряд равен нулю. При этом структура этих зарядов в отсутствии электрического поля может быть двух типов:
во-первых, у ряда диэлектриков в связанных зарядах центр положительного и центр отрицательного зарядов
В результате этого на противоположных поверхностях диэлектрика появятся заряды противоположных знаков, которые получили название поляризационных, а процесс возникновения этих зарядов- явлением поляризации. Процесс поляризации, происходящий с полярными молекулами называется ориентационным. Он зависит от напряженности внешнего электрического поля и от температуры (прямо и обратно пропорционально).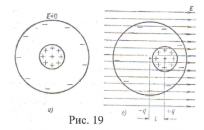
2. Для неполярных молекул диэлектриков при помещении их в электрическое поле происходит деформация атомной структуры-в основном деформа-ция электронных оболочек, хотя и возможно некоторое смещение ядра по направлению вектора электрического поля (рис.19). В результате центр положительного заряда (ядра) и центр отрицательных зарядов (электронов) уже не совпадают и такие молекулы превращаются в диполи, вектора электрических моментов которых будут направлены по полю вектора Е и на поверхностях диэлектрика появятся заряды противополож-ных знаков-произойдет поляризация, получившая название деформационной (электронной).
Если диэлектрик имеет пространственную кристаллическую ионную решетку, то при помещении его в электрическое поле происходит смещение ионных решеток с образова-нием диполей. Такой тип поляризации называется ионной.
|
14.Результирующее поле в диэлектрике. Ослабление поля в диэлектрике. Физ.смысл относительной д.проницаемости.
Сам диэлектрик создает собственное эл.поле напряженностью Е1, направленное навстречу внешнему полю. Результирующее поле: 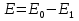 и которое является тем полем, которое существует внутри диэлектрика, т.е. напряженность поля внутри диэлектрика меньше напряженности поля вне его. и которое является тем полем, которое существует внутри диэлектрика, т.е. напряженность поля внутри диэлектрика меньше напряженности поля вне его.
Величина, указывающая во сколько раз кулоновская сила взаимодействия в вакууме больше, чем в данной среде, называется относительная диэлектрическая проницаемость среды (относительная постоянная среды)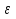 . . 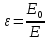
|
15.Вектор электростатической индукции (эл.смещения). Линии электростатической индукции.
Физ.величина вектор электростатической индукции или вектор смещения 
Это значит, что вектор смещения есть вектор, имеющий то же направление, что и вектор Е, но отличающийся от него по величине в 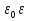 раз, при этом вектор D не зависит от диэлектрических свойств среды. раз, при этом вектор D не зависит от диэлектрических свойств среды.
Для точечного заряда: 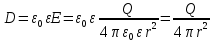
|
Сферический конденсатор (рис. 29) представляет две проводящие сферы радиусамиR1 и R2, между которыми находится диэлектрик. Если зарядить внутреннюю сферу зарядом +Q,то по индукции на внешней поверхности отводятся к земле). Между обкладками сферического конденсатора возникнет разность потенциалов 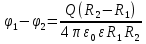 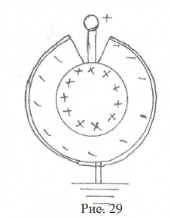
Тогда, 
|
21.Конденсаторы. Электроемкость плоского конденсатора.
Системы, емкость которых не зависит от окружающих тел называют конденсаторами.
Плоский конденсатор состоит из двух тонких металлических пластин (обычно алюминиевая фольга), между которыми прокладывается тонкий слой диэлектрика (слюда, бумага, пропитанная диэлектрическим веществом и т.д.). Для компактности плоский конденсатор сворачивают в рулон.
Зарядим конденсатор, для чего его пластины присоединим к источнику постоянного тока. Тогда на
заряд на каждой из пластин
одной пластине будет потенциал ϕ1 , а на другой равный, но противоположный по знаку потенциал ϕ2 и заряд на каждой из пластин Q.
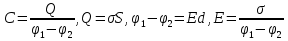
|
18.Свободные заряды в проводниках. Классификация проводиков. Поведение проводников в эл.поле. Индуцированные заряды. Условия равновесия зарядов в нейтральных проводниках с избытком зарядов.
Проводники электрического тока делят на две группы: проводники первого рода- металлы и проводники второго рода- электролиты. Во всех проводниках имеются свободные носители электрических зарядов.
В узлах кристаллической решетки металлов находятся положительные ионы, совершающие колебательное движение. Между ионами в кристаллической решетке перемещаются свободные электроны. Общий заряд свободных электронов равен общему заряду положительных ионов решетки. Направленный перенос свободными электронами зарядов не приводит к заметному переносу массы вещества.
В проводниках второго рода - электролитах переносчиками зарядов являются положительные и отрицательные ионы и перенос ими зарядов приводит к переносу заметной массы и осаждению ее на тех поверхностях, где ионы нейтрализуются.
Рассмотрим поведение проводников-металлов в электрическом поле. Пусть имеется незаряженный проводник; внесем его в электрическое поле напряженностью Е0. В момент времени t=0 на электроны действует сила F=еE0 и электроны начинают движение (навстречу вектору Е) и будут оседать на левой стороне поверхности проводника, создавая на ней отрицательный заряд, который называют индуцированным.
|
25.Энергия заряженного проводника. Энергия заряженного конденсатора. Энергия эл.поля. Объемная плотность энергии эл.поля.
Заряженный проводник обладает энергией, что обнаруживается при разряде : искра дает нам световую (лучистую), механическую и другие виды энергии, что совершенно понятно, потому что на зарядку тела была затрачена работа. Величину этой полной работы можно подсчитать, если взять интеграл от элементарной работы, затраченной на перемещение бесконечно малого заряда из бесконечности на тело, у которого в данный момент
имеется некоторый потенциал:
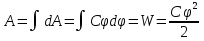
Энергия заряженного конденсатора вычисляется как сумма энергий двух заряженных проводников с потенциалами ϕ1 и ϕ2, с зарядами +Q, и - Q: 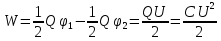
Энергия электрического поля. В пространстве действие электрического поля на заряды обнаруживается, когда вблизи нет ни зарядов, ни заряженных тел (они находятся на достаточно далеком расстоянии от точки). 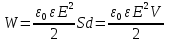
Используется характеристика объемная плотность энергии (в Дж/м ):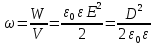
|
23.Соединения конденсаторов.
Для увеличения или уменьшения емкости систем в радиотехнических и электротехнических устройствах используется соединение конденсаторов в группы: параллельное, последовательное и смешанное соединение.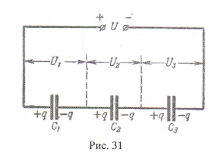 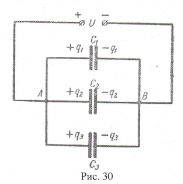
Параллельное соединение конденсаторов (рис. 30).
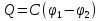
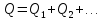

Последовательное соединение конденсаторов (рис. 31)
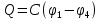
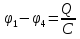

При смешанном виде соединения сначала определяется емкость последовательно соединенных участков, а затем параллельных, затем общая.
|
20.Эл.емкость проводника. Емкость уединенного проводника. Единицы электроемкости.
Коэффициент С- называют электроемкостью проводчика или просто емкостью.
Электрическая емкость уединенного проводника есть скалярная величина характеризующая способность проводника накапливать электрический заряд и равная отношению заряда проводника к его потенциалу в предположении, что все другие проводники бесконечно удалены и что потенциал в бесконечности равен нулю. 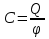
Единицы электрической емкости. В системе СИ 1 фарада (Ф): 1Ф=1Кл/1В.
|
24.Энергия системы неподвижных точечных зарядов.
На электрический заряд, помещенный в электрическое поле, действуют силы, которые могут, перемещая его, выполнить работу. Таким образом, заряд, помещенный в поле, обладает энергией. Величина этой энергии может быть рассчитана по величине работы, совершаемой силами поля при перемещении заряда из точки, где он находится, в бесконечность. Эта энергия равна заряду, умноженному на потенциал точки, в которой он находится (при условии, что потенциал в бесконечной точке равен нулю), 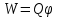
Пусть имеем два точечных заряда Q1 и Q2 :
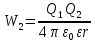
Она равна работе, совершаемой силами поля первого заряда при удалении второго заряда в бесконечность.
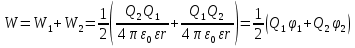
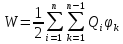 ,ϕk-это алгебраическая сумма потенциалов, создаваемых в точке, где находится данный i - тый заряд всеми другими зарядами (кроме i - того). ,ϕk-это алгебраическая сумма потенциалов, создаваемых в точке, где находится данный i - тый заряд всеми другими зарядами (кроме i - того).
|
22.Емкость сферического и цилиндрического конденсаторов.
Цилиндрический конденсатор представляет собой два проводящих коаксиальных цилиндра, пространство между которыми заполнено диэлектриком. Пусть длина цилиндров будет 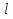 , радиус внутреннего цилиндра r1, внешнего г2. Зарядим конденсатор, сообщив разноименные заряды цилиндрам +Q и - О. , радиус внутреннего цилиндра r1, внешнего г2. Зарядим конденсатор, сообщив разноименные заряды цилиндрам +Q и - О. 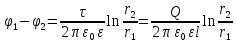 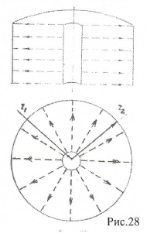
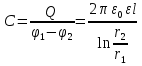
Примером цилиндрических конденсаторов являются коаксиальные кабели (телевизионные, электрокабели).
| |
 Скачать 0.61 Mb.
Скачать 0.61 Mb.