Интегрирование дифференциальных уравнений с. 1) Если аналитические функции x в окрестности точки x0, то решения уравнения (1) тоже будут аналитическими функциями в точке x0 и, следовательно, их можно представить в виде ряда
 Скачать 256 Kb.
|
|
Интегрирование дифференциальных уравнений с помощью рядов. Теорема 1. Об аналитичности решения. Пусть дано линейное уравнение второго порядка:  (1)Если  - аналитические функции x в окрестности точки x0 , то решения уравнения (1) тоже будут аналитическими функциями в точке x0 и, следовательно, их можно представить в виде ряда:  . (2) Теорема 2. О разложимости решения в обобщенный степенной ряд. Если (1) удовлетворяет условиям теоремы 1, но при этом x=x0 является нулем порядка s для функции  , где s-конечное число, нулем порядка s-1 или выше для  и нулем порядка не ниже s-2 для  (s>2). Тогда существует хотя бы одно нетривиальное решение (1), которое может быть представлено в виде обобщенного степенного ряда: , (3)где  - некоторое действительное число. Замечание.Второе линейно независимое решение (1) тоже имеет вид (3) или может быть представлено в виде произведения обобщенного степенного ряда и  .Замечание.В конкретных задачах подбирают степенной или обобщенный степенной ряд, формально удовлетворяющий уравнению (1). При подстановке решения в уравнение (1) мы должны получить тождество, которое позволит определить коэффициенты  или и . А далее полученный ряд исследуется на сходимость и вычисляется его сумма, которая и будет частным решением (1). Линейная комбинация частных решений в виде бесконечных рядов – общее решение (1).Перепишем (1) в виде:  . (4)Замечание.С помощью замены переменных можно свести процесс поиска решения в окрестности точки  к поиску решения в окрестности точки x=0. В дальнейшем будем, не нарушая общности, считать, что решение ищется в точке x=0. Это решение имеет вид: (5)Решение (5) подставим в уравнение (4), приведем подобные и приравняем коэффициенты при одинаковых степенях x. Т.о. получим рекуррентные соотношения, позволяющие определить коэффициенты . Первые одно или два уравнения позволяют вычислить . Эти соотношения называются определяющими. Теорема Фукса (позволяет определить решение в виде (5)). Пусть дано дифференциальное уравнение (4), такое, что функции  имеют полюсы в точке . Тогда решения этого уравнения можно искать в виде обобщенного степенного ряда (3) при условии, что  и  остаются конечными в x0. Пример. Пусть дано (4) и 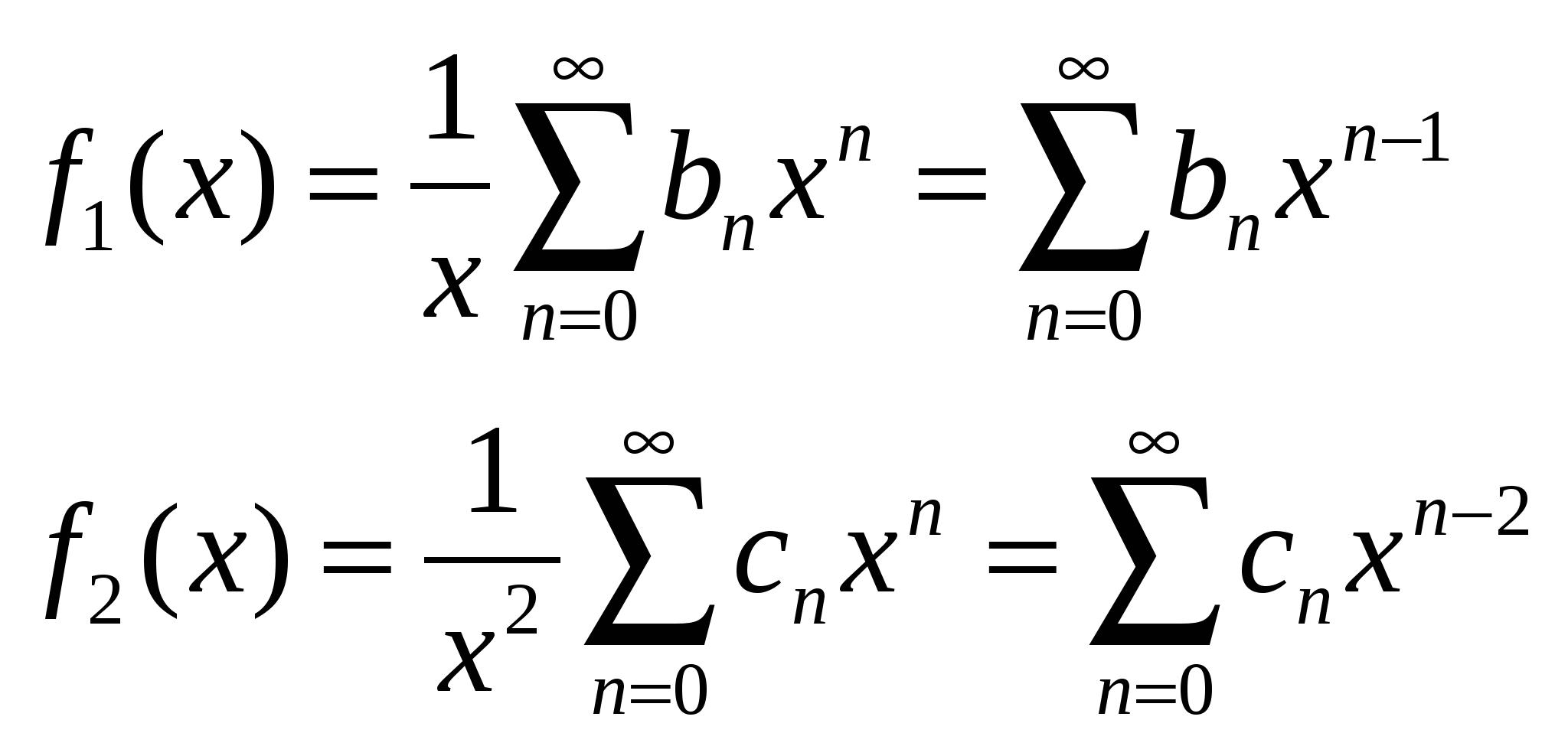удовлетворяют условиям теоремы Фукса, т.е. могут быть представлены в виде: .Подставим решение (5) в (4), учитывая выражения для 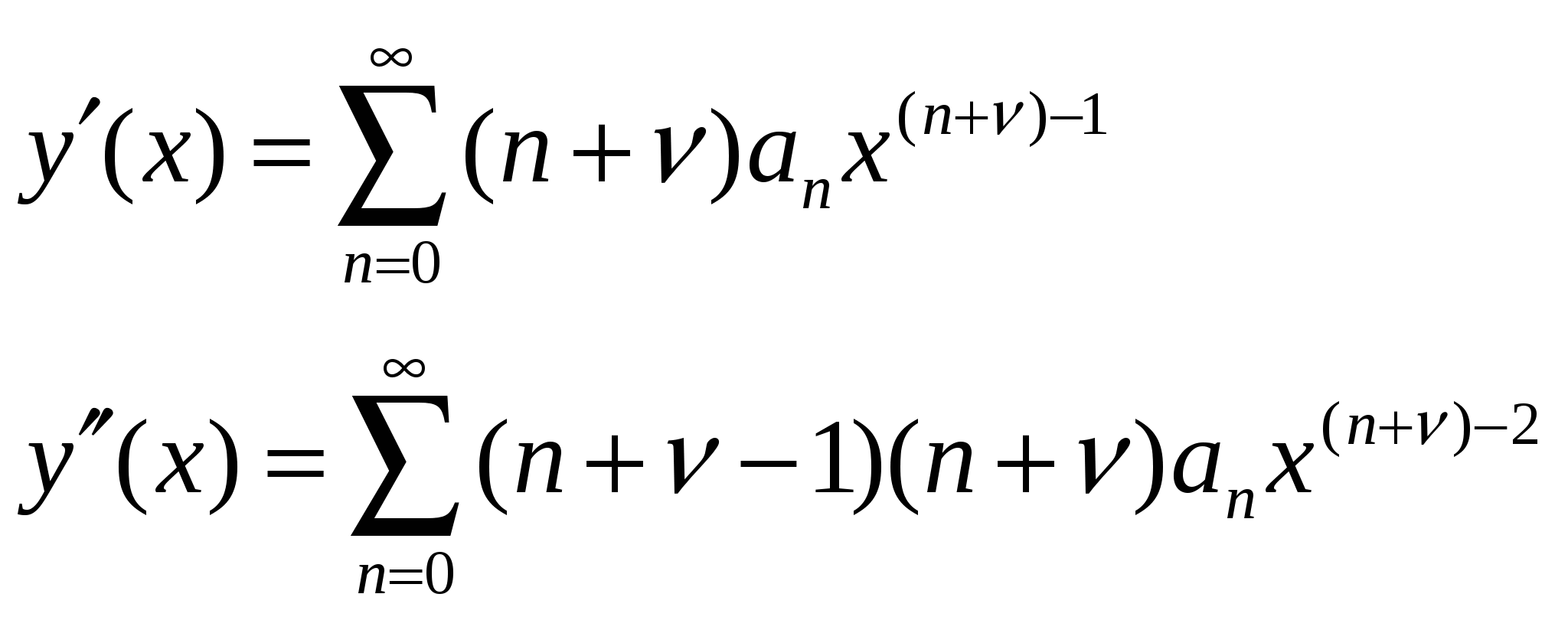. Вычислим производные от решения и тоже подставим в (4): .В итоге получим:  (*)Минимальная степень x в (*) – (  ). Вычислим коэффициенты при  , т.е. при n=0: .Квадратное уравнение относительно 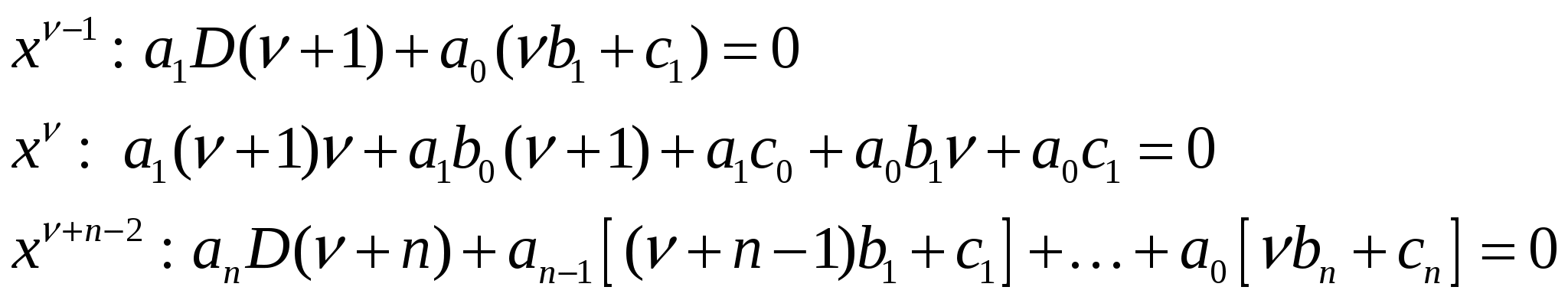 – определяющее соотношение, решив его, получим . В общем виде, выписав соотношение при  , найдем зависимости для . Из определяющего уравнения мы находим два значения  .1)Предположим, что 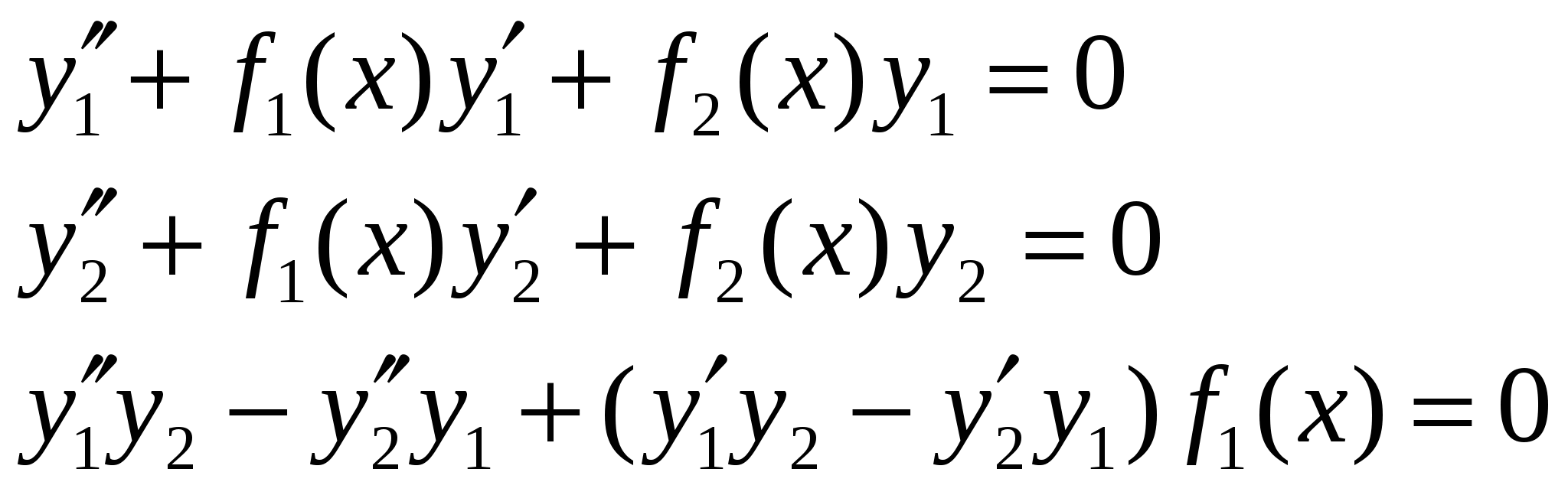 не равны между собой и их разность не равна целому числу. Тогда можно последовательно вычислить два ряда коэффициентов соответствующих  . После этого получим два обобщенных степенных ряда типа (5), которые определяют линейно-независимые решения уравнения (4).2)Пусть  , значит по соотношению (5) можно найти только одно решение (4), а второе будем искать с помощью следующего приема. Пусть  и  линейно-независимые решения (4), -произвольные функции. Подставим и в уравнение (4) и исключим из него  : Левая часть этого уравнения, с точностью до множителя 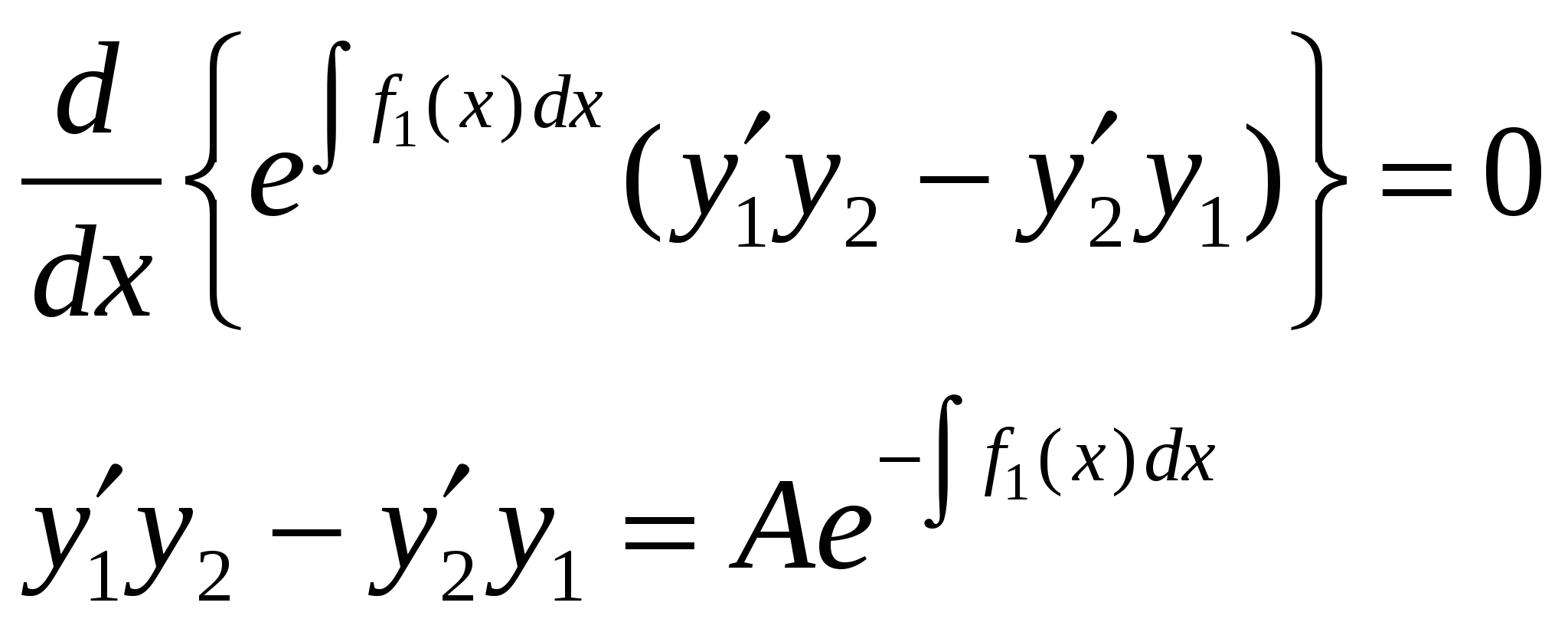 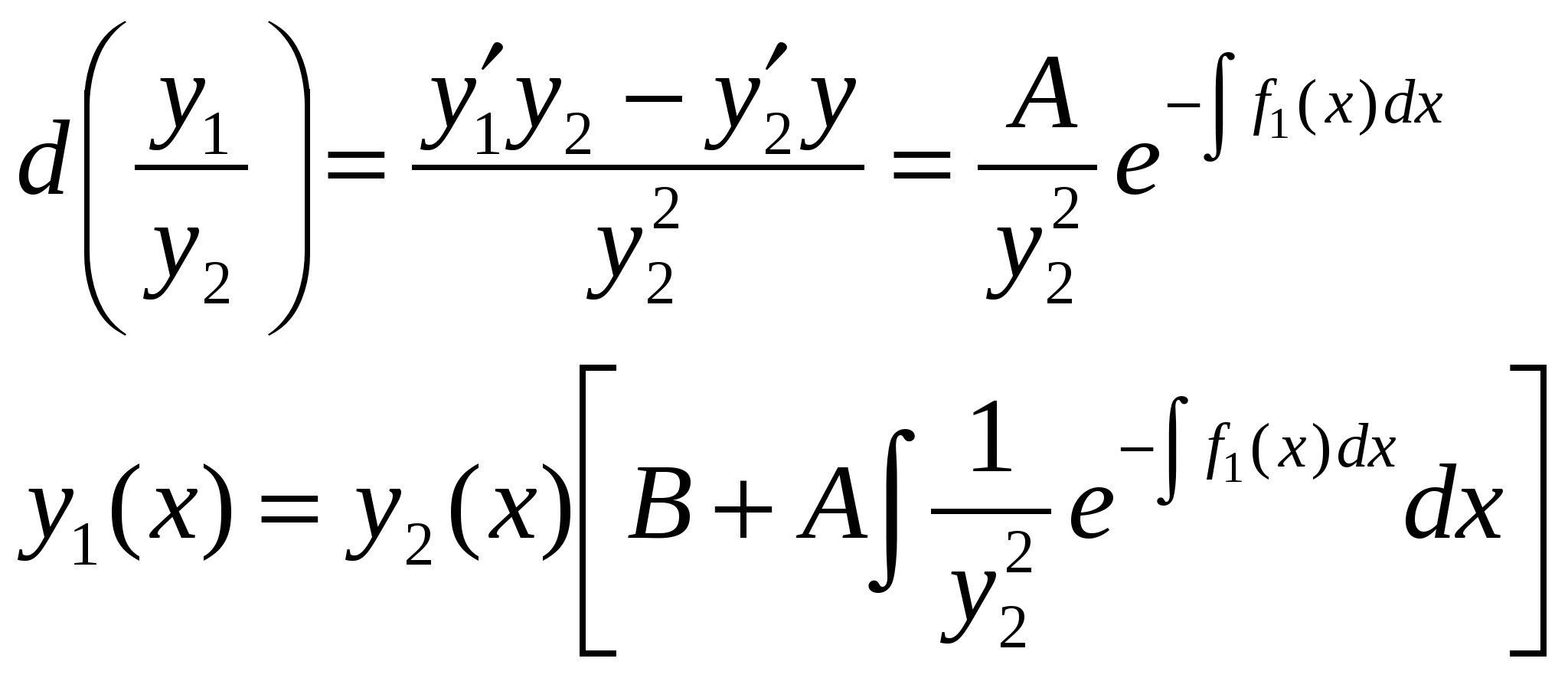будет производной от выражения: . .3)Пусть  , но  натуральное число ( ). Тогда мы можем выписать коэффициенты ряда соответствующие  :  . Для ряда, который соответствует  , процесс вычисления коэффициентов обрывается на номере n-1. Соотношения, которые мы получаем, связывают коэффициент с  … .  ,  .Значит, от этого соотношения остается равенство:  Если уже вычисленные коэффициенты  не удовлетворяют этому равенству, то найти второе частное решение вида (5) - невозможно, т.е. предложенный метод не позволяет определить общий интеграл. Если же это соотношение выполняется, тогда можно все коэффициенты  выразить через .Тогда остается неопределенным и ряд для корня строится с точностью до двух параметров  .Пример. Гипергеометрический ряд.  - постоянные параметры.Это уравнение имеет две особые точки x=0 и x=1, т.е. мы можем искать решение уравнения в виде ряда в окрестности 0 или 1, т.к. для обеих точек условие теоремы Фукса выполняются. Будем искать решение в виде: 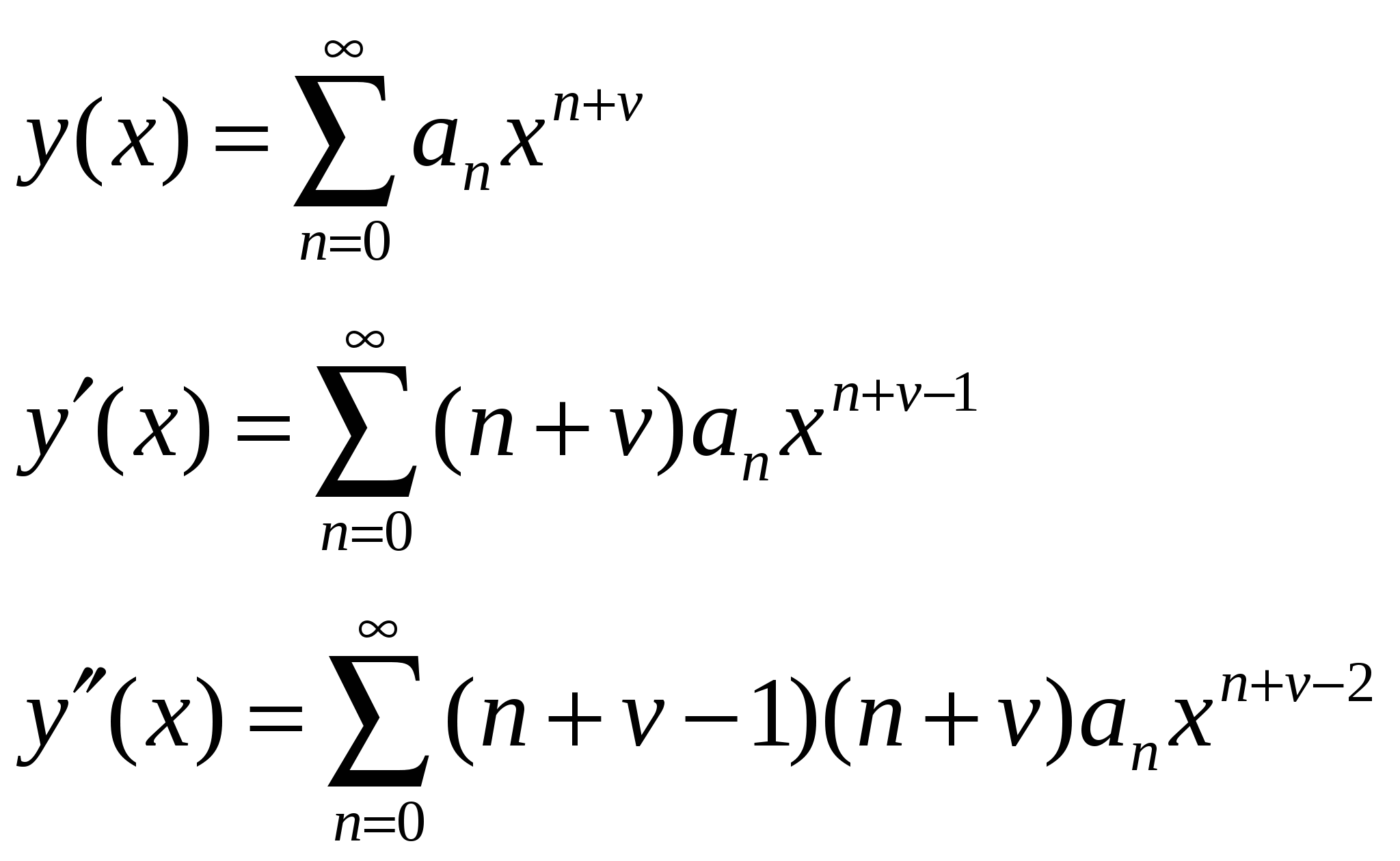 Подставим в исходное уравнение: 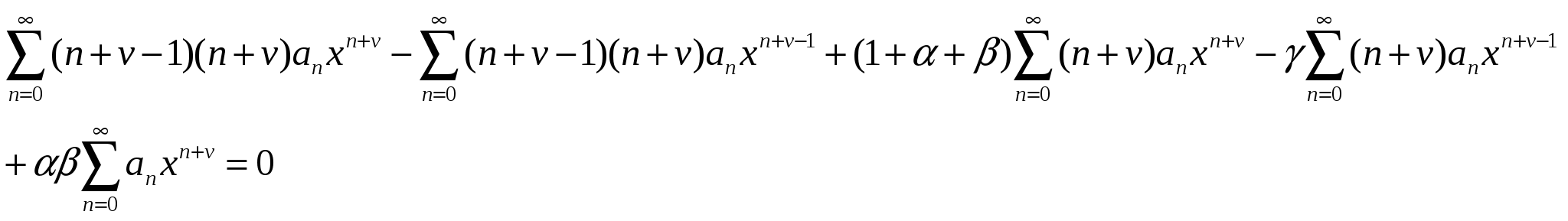 Выпишем коэффициенты при соответствующих степенях x: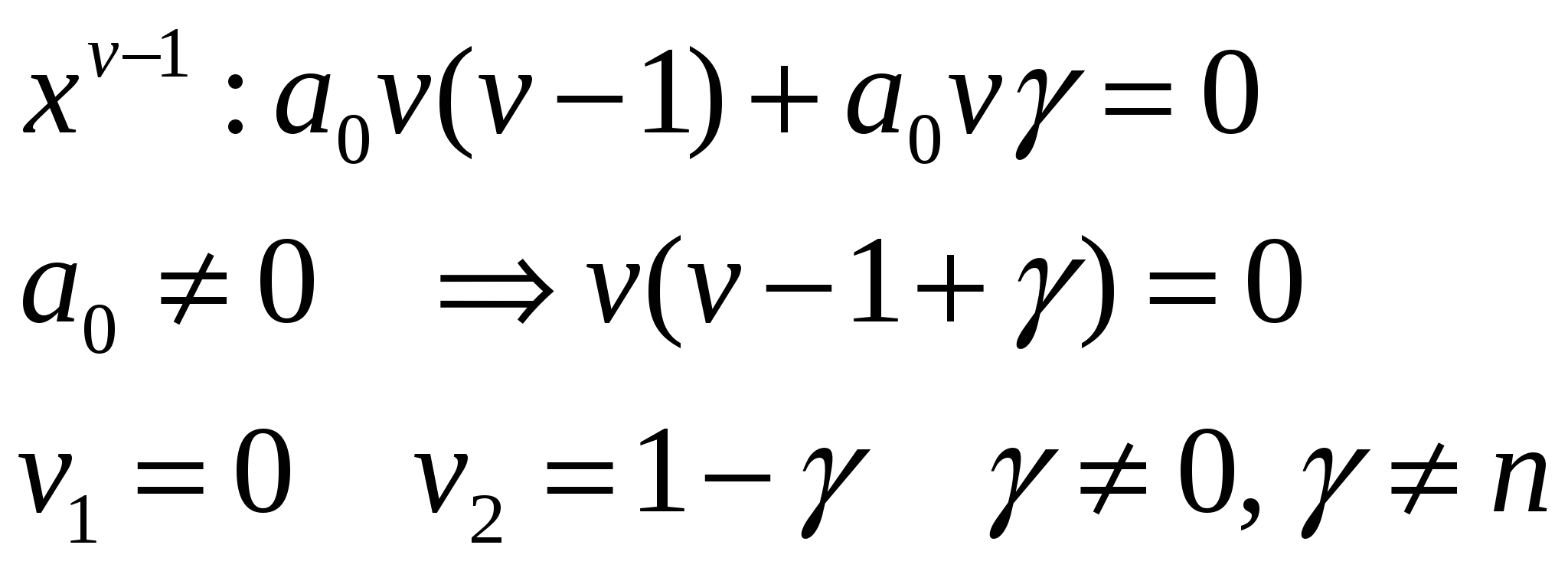   В этом случае каждое решение может быть представлено в виде обобщенного степенного ряда. 1).v1=0,   Гипергеометрический ряд Гаусса. Этот ряд сходится абсолютно при любых значениях  , если |x|<1, и сходится при |x|=1 абсолютно, если  . Обозначается этот ряд следующим образом:  , где F-гипергеометрическая функция Гаусса.2).  , тогда:  Тогда общее решение исходного уравнения:  .Уравнение Бесселя.  , (1)где  - произвольное действительное число, называется уравнением Бесселя. В некоторых случаях может быть комплексным, но тогда предполагается неотрицательной его действительная часть.Для (1) выполняется условие теоремы Фукса - x=0 особая точка. Значит, решение будем искать в виде:  (2)Если подставить (2) в (1), то получим следующие соотношения при степенях x. 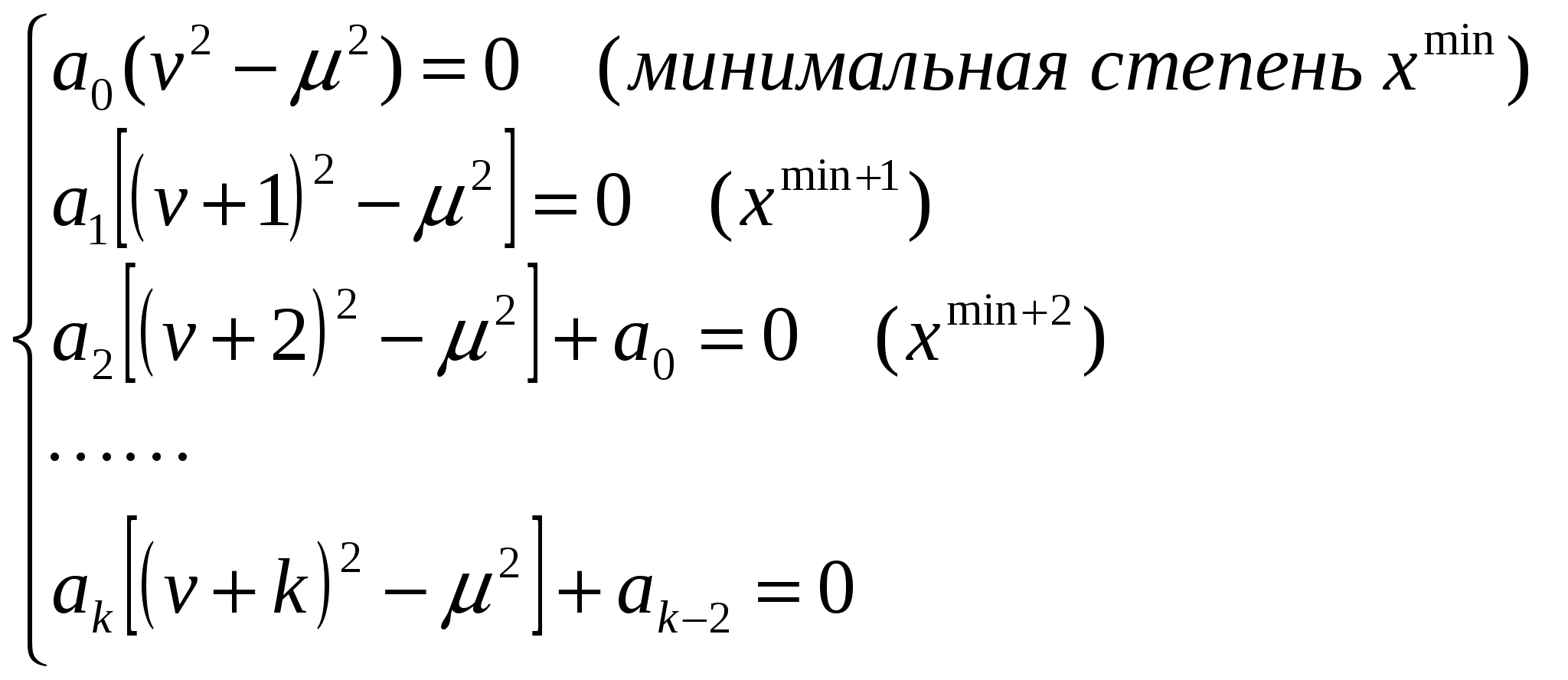 (3)В качестве определяющего соотношения выберем первое уравнение системы, тогда  , (4) , (5)  . (6)Рассмотрим второе равенство из (3):    . (7)Т.к.  , а каждое  определяется через  , то все нечетные коэффициенты будут равны нулю. А все четные коэффициенты будут определяться по формуле (6). . (8)В (8) выразим все коэффициенты через : .Воспользуемся свойствами гамма-функции (  ) и запишем коэффициенты в компактной форме: , (9) . (10)Если  , то  . (11) . (12)Определение. Ряд (2) соотвествующий  , с коэффициентом , определяющемся по формуле (9) и  - по формуле (10) – называется функцией Бесселя первого рода -ого порядка. (13)Если , то второе линейно-независимое решение имеет вид: (14)Ряды (13) и (14) сходятся для любых x. Заметим, что (14) определяет функцию Бесселя  только для дробных значений , поскольку при целых отрицательных коэффициенты этого ряда не существуют. Но т.к. функция Бесселя непрерывна, мы можем продолжить ее и для =-n, где n– целое число. Т.е.  . В этом случае мы получим только одно линейно-независимое решение.Периодические решения дифференциальных уравнений. Дано дифференциальное уравнение вида:  (1) Пусть нужно найти периодическое решение некоторого дифференциального уравнения, тогда естественно искать решение в виде соответствующего ряда Фурье.  . (2)Если решение уравнения (1) имеет период Т, то тогда правая часть (1) тоже периодическая функция с периодом Т. Подставим известное решение  в уравнение (1) и, заменив х=х+Т, получим: Воспользуемся тем, что решение имеет период Т, т.е.:  Для того, чтобы последнее выражение было тождеством необходимо и достаточно, чтобы F была периодической, т.е. функция F вдоль интегральной кривой  имела период Т по явно входящему аргументу х.Замечание. Если правая часть (1) при любом выборе  , не является периодической функцией по х, то периодического решения (1) не существует. Замечание. Если функция F не зависит явно от аргумента х, то F можно рассматривать как периодическую функцию от х любого периода и поэтому у уравнения (1) будут существовать периодические решения любого периода. Пусть дано уравнение  (3)и требуется найти периодическое решение этого уравнения. Предположим, что f(x) – периодическая функция с периодом 2. Раз правая часть имеет период 2, то мы ее можем представить в виде ряда Фурье.  (4) (5)Подставим (4) и (5) в (3):  Выпишем коэффициенты: 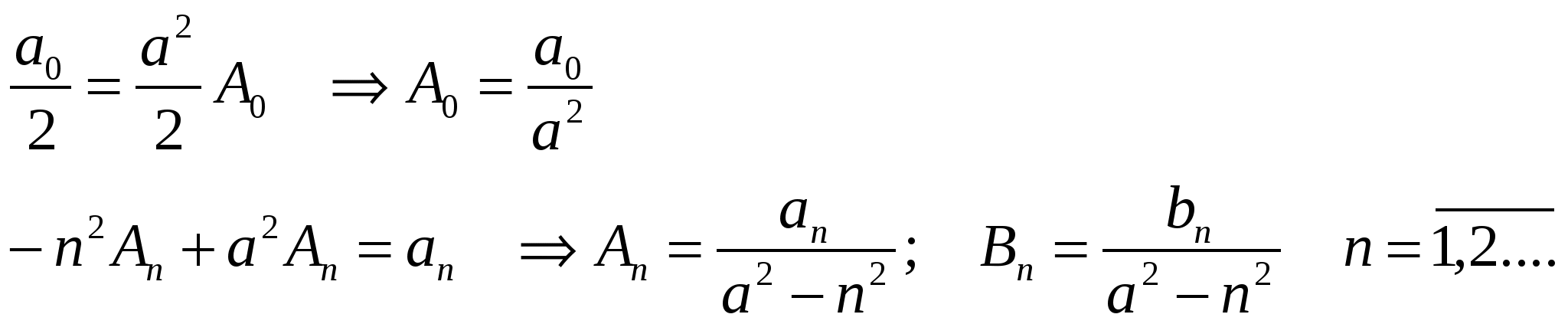 (6)Периодическое решение полностью определено. Замечание. Ряд (5) с определенными коэффициентами (6) сходится и допускает двукратное дифференцирование. В силу того, что f(x) непрерывна, ряд сходится равномерно и значит решение y(x) – сумма этого ряда. Замечание. Если коэффициенты  в периодическом решении  и число а мало отличается от целого числа n, тогда наступает явление резонанса, т.е. резко возрастает один из коэффициентов  . Если a=n и хоть один из коэффициентов не равен 0, то периодического решения не существует. Если оба коэффициента  , то при a=n периодическое решение уравнения существует. |