ПЗ. 1. Физические основы полета ракеты с переменной массой
 Скачать 443 Kb.
|
|
Содержание Введение…………………………………………………………………………3 1.Физические основы полета ракеты с переменной массой………………..4 1.1.Уравнения Мещерского и Циолковского – основополагающие реактивного движения………………………………………………….…………..4 1.2.Практический смысл уравнений Мещерского………………………….9 2.Преимущества использования языка С++………………………………..12 3. Написание программы «Полет ракеты с учетом изменения ее массы»..14 3.1.Преимущества применения Visual Studio 2010………………………..14 3.2.Моделирование полета ракеты…………………………………………16 Заключение……………………………………………………………………23 Список использованной литературы……………………………………….24 Введение Во все времена человек мечтал летать как птицы. И вот его мечта путем проб и ошибок, постоянного и тщательного изучения окружающего мира осуществилась – он построил самолет. Но человеку свойственно мечтать. И теперь его мечты связаны с тем, как полететь к звездам, к планетам, которые кажутся такими близкими, но оказываются далекими, к другим галактикам. Чтобы осуществить космические полеты писатели-фантасты предлагали самые разные средства для достижения этой цели. В XVII веке появился рассказ французского писателя Сирано де Бержерака о полёте на Луну. Герой этого рассказа добрался до Луны в железной повозке, над которой он всё время подбрасывал сильный магнит. Притягиваясь к нему, повозка всё выше поднималась над Землёй, пока не достигла Луны. А барон Мюнхгаузен рассказывал, что забрался на Луну по стеблю боба. Но все предложенные способы не позволяли человеку преодолеть силу земного притяжения, двигаться в безвоздушном пространстве. И как всегда для решения этой сложнейшей задачи человек обращается к природе, которая подсказывает решение – реактивное движение. Именно реактивное движение является основой современной авиации гражданской и военной, космической техники. 1.Физические основы полета ракеты с переменной массой 1.1.Уравнения Мещерского и Циолковского – основополагающие реактивного движения Идея применения ракеты для решения научных проблем, использование реактивных двигателей для создания движения грандиозных межпланетных кораблей целиком принадлежат Циолковскому. Он родоначальник современных жидкостных ракет дальнего действия, один из создателей новой главы теоретической механики. Классическая механика, изучающая законы движения и равновесия материальных тел, базируется на трех законах движения, отчетливо и строго сформулированных английским ученым Исааком Ньютоном еще в 1687 году. Эти законы применялись многими исследователями для изучения движения тел, масса которых не изменялась во время движения. Были рассмотрены очень важные случаи движения и создалась большая наука — механика тел постоянной массы. Аксиомы механики тел постоянной массы, или законы движения Ньютона, явились обобщением всего предыдущего развития механики. В настоящее время основные законы механического движения излагаются во всех учебниках физики для средней школы. Мы дадим здесь краткое изложение законов движения Ньютона, так как последующий шаг в науке, позволивший изучать движение ракет, был дальнейшим развитием методов классической механики. Первый закон Ньютона, в частных случаях известный еще Галилею и Декарту, формулируется следующим образом: «Всякое материальное тело продолжает пребывать в состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменить это состояние». Этот закон часто называется законом инерции, и он выражает одно из существенных свойств материальных тел. Суть закона инерции состоит в том, что механическое движение данного тела не может возникнуть из ничего, а только под влиянием взаимодействий с другими телами. Изолированное от влияния других тел, всякое материальное тело или находится в покое, или движется прямолинейно и равномерно, сохраняя свое движение. Взаимодействия тел друг с другом, передача движения от одного тела к другому суть причины изменения покоя или равномерного и прямолинейного движения. Движение тела не может исчезнуть и превратиться в ничто, а может быть или передано другому материальному телу как механическое движение, или может превратиться в другие формы движения (например, в тепло). Если m — масса тела, a v — его скорость, то произведение (mv) называют количеством движения тела. Для изолированного тела его количество движения остается постоянным. Изменение количества движения может произойти только под влиянием других тел, или, как говорят в механике, под действием сил. Стремление тела сохранить свое количество движения проявляется на опыте в том, что при встрече движущегося тела с препятствием оно производит тем большее давление, чем больше его скорость и чем больше его масса. Второй закон Ньютона устанавливает меру механического взаимодействия между телами и формулируется так: изменение количества движения пропорционально приложенной движущей силе и происходит по направлению той прямой, по которой эта сила действует. Если должным образом выбрать единицы массы, скорости и времени, то второй закон можно высказать еще в следующем виде: масса тела, умноженная на его ускорение, равняется движущей силе. Направление ускорения совпадает с направлением движущей силы. Таким образом, величину механических взаимодействий между телами мы можем измерять по изменению количества движения, а для тел постоянной массы — по ускорению движущегося тела. Из второго закона Ньютона следует, что одна и та же сила сообщает телам с разными массами (разными весами) разные ускорения. Разные силы сообщают какому-либо выбранному телу ускорения, пропорциональные силам. В современной теоретической механике второй закон Ньютона является той основой, на которой базируются все математические расчеты. Однако следует указать, что второй закон Ньютона справедлив только для тел, масса которых сохраняется постоянной во все время движения. Следовательно, вторым законом Ньютона можно, например, воспользоваться для изучения движения артиллерийского снаряда, но нельзя изучать движение реактивного снаряда. Для тел постоянной массы законы Ньютона и выводы из них подтверждаются всей общественно-производственной практикой человечества, за исключением специальных областей техники, охватываемых механикой теории относительности. Третий закон Ньютона имеет весьма большое значение в теории движения ракет, и его можно высказать в следующей форме: действию всегда есть равное и противоположное противодействие; иначе говоря, взаимные действия тел друг на друга между собою равны и направлены в противоположные стороны. Под реактивным движением понимают движение тела, возникающее при отделении некоторой его части с определённой скоростью относительно тела, например при истечении продуктов сгорания из сопла реактивного летательного аппарата. При этом появляется так называемая реактивная сила, сообщающая телу ускорение. Примером реактивного движения является движение воздушного шарика, из которого вытекает воздух. Оно будет кратковременным, так как реактивная сила действует лишь до тех пор, пока продолжается истечение воздуха. Главная особенность реактивной силы состоит в том, что она возникает без какого-либо взаимодействия с внешними телами. Происходит лишь взаимодействие между ракетой и вытекающей из неё струёй вещества. При истечении продуктов сгорания топлива они за счет давления в камере сгорания приобретают некоторую скорость относительно ракеты и, следовательно, некоторый импульс. Поэтому в соответствии с законом сохранения импульса сама ракета получает такой же по модулю импульс, но направленный в противоположную сторону. Масса ракеты с течением времени убывает. Ракета в полете является телом переменной массы. Для расчета ее движения удобно применить закон сохранения импульса. Получим уравнение движения ракеты и найдём выражение для реактивной силы. Будем считать, что скорость вытекающих из ракеты газов относительно ракеты постоянна и равна  . Внешние силы на ракету не действуют: она находится в космическом пространстве вдали от звезд и планет.Пусть в некоторый момент времени скорость относительно инерциальной системы, связанной со звездами, равна  , а масса ракеты равна  . Через малый интервал времени  масса ракеты станет равной , где  - расход топлива (отношение массы сгоревшего топлива ко времени его сгорания).За этот промежуток времени скорость ракеты изменится на  и станет равной  . Скорость истечения газов относительно выбранной инерциальной системы отсчета равна  , так как до начала сгорания топливо имело ту же скорость, что и ракета.Тогда закон сохранения импульса для системы ракета-газ: 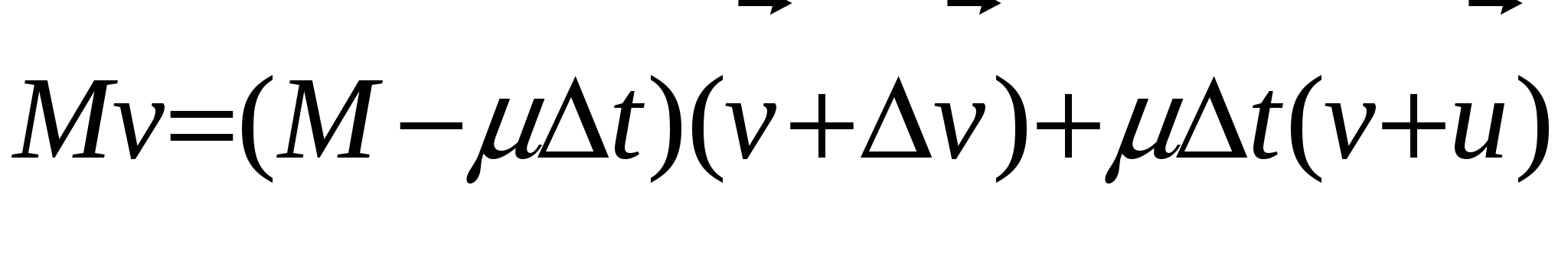 Раскрыв скобки, получим: 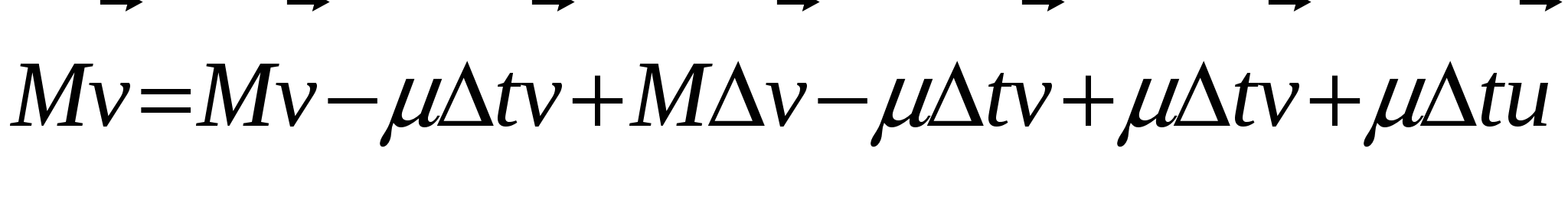 С  лагаемым  можно пренебречь по сравнению с остальными, так как оно содержит произведение двух малых величин (это величина, как говорят, второго порядка малости). После приведения подобных членов будем иметь:  , или Это одно из уравнений Мещерского для движения тела переменной массы, полученное им в 1987 г. Если ввести обозначение  , то уравнение совпадёт по форме со вторым законом ньютона. Однако масса тела здесь не постоянна, а убывает со временем из-за потери вещества.Величина носит название реактивной силы. Она появляется вследствие истечения газов из ракеты, приложена к ракете и направлена противоположно скорости газов относительно ракеты. Реактивная сила определяется лишь скоростью истечения газов относительно ракеты и расходом топлива. Существенно, что она не зависит от деталей устройства двигателя. Важно лишь, что бы двигатель обеспечивал истечения газов из ракеты со скоростью при расходе топлива . Реактивная сила космических ракет достигает 1000 кН.Если на ракету действуют внешние силы, то её движение определяется реактивной силой и суммой внешних сил. В этом случае уравнение запишется так:  .Решил уравнение Мещерского, то есть получил в явном виде формулу, позволяющую в любой момент времени полета ракеты определить ее скорость по известным начальным условиям, великий русский ученый, основоположник отечественной космонавтики К.Э. Циолковский в 1903 году. Выведенная им формула получила название формулы Циолковского:  Здесь - скорость ракеты, когда ее масса стала равна m,  - скорость ракеты на старте, - скорость продуктов сгорания относительно ракеты, ln – символ натурального логарифма, m0 – масса ракеты на старте, m – масса ракеты в момент, когда ее скорость стала равна .Из формулы Циолковского следует, что чем больше топлива сгорит, то есть чем меньше будет оставшаяся масса m, тем большую скорость разовьет ракета. Для увеличения полезной массы ракеты увеличивают скорость истечения газов, подбирая соответствующие виды топлива. Газы, выходящие из ракеты, должны иметь по возможности меньшую молекулярную массу (чем меньше молекулярная масса топлива, тем больше объём газов, образующихся при его сгорании, и, следовательно, скорость их истечения) и быть нагреты до возможно более высокой температуры.  Кроме того, используют несколько последовательно работающих, а затем отбрасываемых ступеней, входящих в состав многоступенчатой ракеты, что позволяет наращивать скорость ракеты в полете. Идея многоступенчатой ракеты была высказана Циолковским. 1.2.Практический смысл уравнений Мещерского Принцип реактивного движения находит широкое практическое применение в авиации и космонавтике. И для космических полетов могут быть использованы только реактивные летательные аппараты, т. е. ракеты (см. рис. 1). 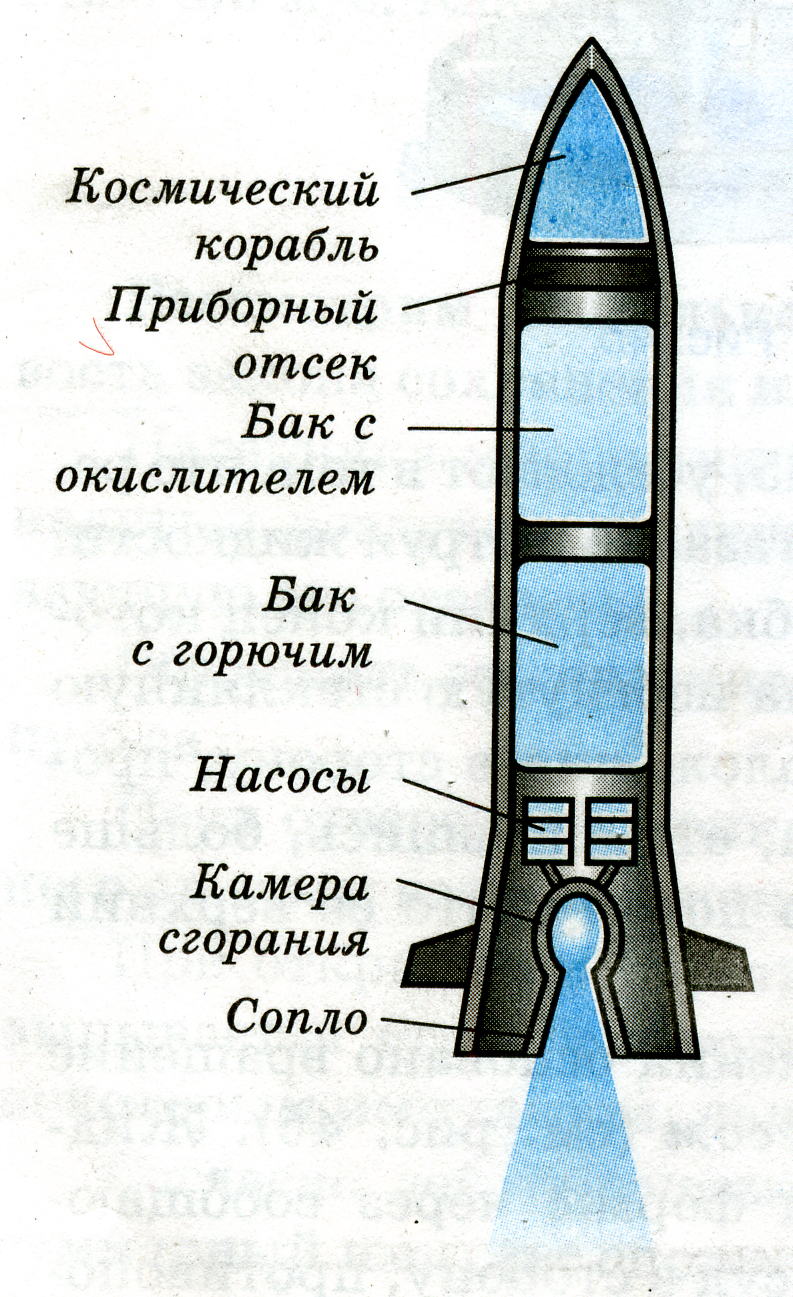 Рис. 1 – Устройство ракеты В любой ракете, независимо от ее конструкции, всегда имеется оболочка и топливо с окислителем. На рисунке изображена ракета в разрезе. Мы видим, что оболочка ракеты включает в себя полезный груз (в данном случае это космический корабль), приборный отсек и двигатель (камера сгорания, насосы и пр.). Основную массу ракеты составляет топливо с окислителем (окислитель нужен для поддержания горения топлива, поскольку в космосе нет кислорода). Топливо и окислитель с помощью насосов подаются в камеру сгорания. Топливо, сгорая, превращается в газ высокой температуры и высокого давления. Благодаря большой разности давлений в камере сгорания и в космическом пространстве, газы из камеры сгорания мощной струей устремляются наружу через раструб специальной формы, называемый соплом. Назначение сопла состоит в том, чтобы повысить скорость струи. Дело в том, что от этой скорости зависит скорость ракеты. Но помимо скорости истечения газа существуют и другие факторы, от которых зависит скорость движения ракеты. Чтобы преодолеть притяжение Земли, ракеты должны развивать огромную скорость. Космические ракеты-носители обычно состоят из двух и более ступеней. На каждой ступени имеется двигатель и запас топлива. Нижняя ступень разгоняет ракету до тех пор, пока не кончится ее топливо. Затем она отделяется и падает, после чего включается двигатель второй ступени, и т.д. Но если же корабль должен совершить посадку, то третья ступень используется для торможения корабля перед посадкой. При этом ракету разворачивают на 180°, чтобы сопло оказалось впереди. Тогда вырывающийся из ракеты газ сообщает ей импульс, направленный против скорости ее движения, что приводит к уменьшению скорости и дает возможность осуществить посадку. 2.Преимущества использования языка С++ При разработке языка С++ одним из важнейших критериев выбора была простота. Когда возникал вопрос, что упростить: руководство по языку и другую документацию или транслятор, - то выбор делали в пользу первого. Огромное значение придавалось совместимости с языком С, что помешало удалить его синтаксис. В С++ нет типов данных и элементарных операций высокого уровня. Например, не существует типа матрица с операцией обращения или типа строка с операцией конкатенации. Если пользователю понадобятся подобные типы, он может определить их в самом языке. Программирование на С++ по сути сводится к определению универсальных или зависящих от области приложения типов. Хорошо продуманный пользовательский тип отличается от встроенного типа только способом определения, но не способом применения. Из языка исключались возможности, которые могут привести к накладным расходам памяти или времени выполнения, даже если они непосредственно не используются в программе. Например, было отвергнуто предложение хранить в каждом объекте некоторую служебную информацию. Если пользователь описал структуру, содержащую две величины, занимающие по 16 разрядов, то гарантируется, что она поместится в 32-х разрядный регистр. Язык С++ проектировался для использования в довольно традиционной среде, а именно: в системе программирования С операционной системы UNIX. Но есть вполне обоснованные доводы в пользу использования С++ в более богатой программной среде. Такие возможности, как динамическая загрузка, развитые системы трансляции и базы данных для хранения определений типов, можно успешно использовать без ущерба для языка. Типы С++ и механизмы упрятывания данных рассчитаны на определенный синтаксический анализ, проводимый транслятором для обнаружения случайной порчи данных. Они не обеспечивают секретности данных и защиты от умышленного нарушения правил доступа к ним. Однако, эти средства можно свободно использовать, не боясь накладных расходов памяти и времени выполнения программы. Учтено, что конструкция языка активно используется тогда, когда она не только изящно записывается на нем, но и вполне по средствам обычным программам. 3. Написание программы «Полет ракеты с учетом изменения ее массы» 3.1.Преимущества применения Visual Studio 2010 Microsoft Visual Studio 2010 - средство для разработчиков ПО, которое позволяет решать основные задачи разработки: система упрощает создание, отладку и развёртывание приложений на различных платформах, включая SharePoint и облачную среду. Мощные средства редактирования и визуального дизайна позволяют реализовать самые смелые замыслы. Visual Studio открывает новые возможности для приложений за счёт использования вычислительных мощностей локального компьютера и облака. Кроме того, Visual Studio является интегрированной средой, в которой разработчики могут использовать уже имеющиеся навыки для написания кода, отладки, модульного тестирования и развертывания непрерывно расширяющейся номенклатуры типов приложений. Visual Studio упрощает реализацию общих задач и обеспечивает индивидуальный подход, что позволяет разработчикам максимально использовать возможности базовых платформ. Мощные инструменты Visual Studio помогают быстро создавать высококачественный код. Интегрированная поддержка разработки через тестирование и новые инструменты отладки ПО для многоядерных процессоров позволяют без труда находить и устранять дефекты, обеспечивая создание высококачественного решения. Visual Studio включает функцию поддержки нескольких мониторов, которая позволяет наиболее удобно организовать работу. Независимо от сложности проекта Visual Studio можно использовать для реализации идей и решений для широкого спектра платформ, включая Windows, Windows Server, веб-среду, облачную среду, Office и SharePoint и многое другое. Microsoft Visual Studio 2010 Professional - интегрированная среда, упрощающая создание, отладку и развертывание приложений. Дайте волю фантазии и реализуйте свое видение с помощью мощных редакторов и новейших методов координирования совместной деятельности разработчиков и дизайнеров. Работайте в персонализированной среде, создавайте приложения для любых платформ, включая Microsoft SharePoint и Windows Azure, используйте для написания кода уже имеющиеся навыки, ускоряя тем самым процесс разработки. Интегрированная поддержка разработки через тестирование и новые инструменты отладки позволяют быстро и без труда находить и устранять ошибки, обеспечивая высокое качество решений. Настройка рабочего места. Написание программного кода часто требует одновременной работы с несколькими конструкторами и редакторами. Visual Studio 2010 Professional помогает разработчику организовать цифровое окружение благодаря поддержке нескольких мониторов, что упрощает работу над программами. Обозреватель SharePoint. С помощью обозревателя SharePoint подключатесь к имеющемуся серверу SharePoint и просматривайте из Visual Studio его артефакты, в том числе пользовательские списки, библиотеки документов и Веб-части. Создание приложений для Windows 7. Visual Studio 2010 Professional включает встроенные инструменты разработки для Windows 7, в том числе такие компоненты пользовательского интерфейса, как мультисенсорный ввод и лента, которые составляют основу передовой технологии Windows 7. Простое создание приложений на базе RIA и WPF. Новая функция привязки данных перетаскиванием (в Windows Presentation Foundation) и конструкторы Silverlight упрощают и ускоряют построение приложений Windows и многофункциональных интернет-приложений (Rich Internet Applications, RIA) для специалистов по проектированию и разработке. Упрощение развертывания веб-приложений. Перемещение веб-приложений в производственную среду одним щелчком мыши. Visual Studio 2010 Professional выполняет перенос кода, параметров IIS и схемы базы данных на целевой сервер. 3.2.Моделирование полета ракеты Рассмотрим основные этапы написания программы (консольного приложения) на Visual Studio 2010. Используем возможности графической библиотеки OpenGL в среде MS Visual Studio и GLUT (OpenGL Utility Toolkit) при визуализации результатов моделирования на языке С++. Для платформонезависимой работы с окнами используем библиотеку GLUT. Библиотека GLUT упрощает работу с OpenGL. Для того чтобы программа запускалась на Visual Studio надо сообщить системе, что используется GLUT. Настройка выглядит следующим образом: 1.Открыть любой браузер и ввести следующюю ссылку на адресной строке: https://www.opengl.org/resources/libraries/glut/ 2. Распаковать то, что скачали в общую папку. 3. Из этой папки копируем файл glut32.dll в системную папку (Если на компьютере x86 архитектура, то в C:\Windows\System32. А если на компьютере х64 архитектура, то в C:\Windows\SysWOW64). 4. Glut32.lib копируем в папку lib, куда был установлен Visual Studio. (C:\Program Files (x86)\Microsoft Visual Studio 12.0\VC\lib) 5. glut.h копируем в папку Include (C:\Program Files (x86)\Microsoft Visual Studio 12.0\VC\include) Непосредственно сам код: Плотность вблизи поверхности Земли double ro = 1.29; Ускорение свободного падения double g = 9.8; Изменение времени в программе double dt = 0.1; Константа уравнения движения double c = 0.45; Коэффициент пропорциональности зависимости плотности атмосферы double b = 0.00129; Сила тяги реактивного двигателя double F ; Сопротивление движению double s = 20; Расход топлива double alpha; Начальная масса ракеты double m0 ; Конечная масса (т.е. масса полезного груза, выводимого на орбиту) double mk ; Соответственно масса топлива, ускорение ракеты, скорость ракеты, высота полета ракеты, время полета ракеты и константа реактивного движения double m, a, v, h, t, k; Рисуем траекторию тела брошенного под углом к горизонту с учетом сопротивления среды void render_scene(){ Очищаем текущим цветом glClear(GL_COLOR_BUFFER_BIT); Рисуем координатную систему и задаем цвет рисовки красным glLineWidth(4.0); glColor3d(1.0, 1.0, 1.0); glBegin(GL_LINES); glVertex2d(0.0, 0.0); glVertex2d(1.4, 0.0); glEnd(); glBegin(GL_LINES); glVertex2d(0.0, 0.0); glVertex2d(0.0, 1.4); glEnd(); Выводим задаваемые параметры на консоль cout << "F = "; cin >> F; cout << "m0: "; cin >> m0; cout << "mk: "; cin >> mk; cout << "alpha: "; cin >> alpha; cout << "k = "; cin >> k; for (i = 0; i <= k; i = i + 1){ F = F + F*0.5; v = 0; h = 0; t = dt; double tk = ((m0 -mk) / alpha); glColor3d(i/10.0, 1.0 - i/10.0, 1.0); glBegin(GL_POINTS); Решаем системууравнений while ((t <= tk) && (v <= 1.0)){ m = m0 - alpha*t; a = (F - m*g - (1 / 2)*c*ro*exp(-b*h)*s*v*v) / m; v = v + a*dt / 7800; h = h + v*dt; glVertex2d(t / tk, v); t += dt; } glEnd(); glutSwapBuffers();} Для инициализации GLUT в начале программы надо вызвать glutInit (&argc, argv). Для задания режима дисплея вызывается glutInitDisplayMode (режим). glutInit(&argc, argv); glutInitDisplayMode(GLUT_DOUBLE | GLUT_RGB); Создание окна для отрисовки glutInitWindowSize(640, 480); glutInitWindowPosition(20, 20); glutCreateWindow("Полет ракеты"); Вызов обратных функций glutDisplayFunc(render_scene); glutReshapeFunc(change_size); Initialise(); Запускаем оболочку GLUT glutMainLoop(); Скомпилируем программу и запустим ее. Смоделируем зависимость v(t) от времени (первая кривая слева) и H(t) (вторая кривая справа) (рис. 2-3). 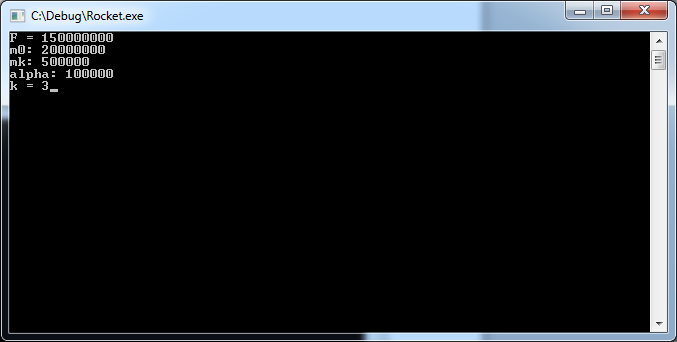 Рис. 2 – Задание параметров 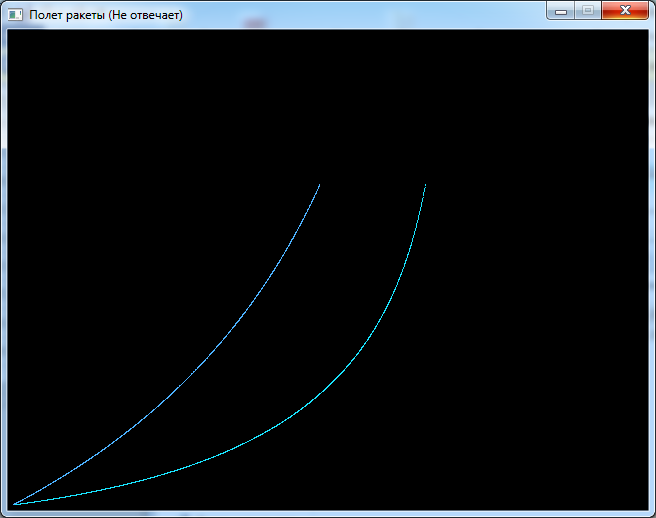 Рис. 3 – Зависимость v(t) Смоделируем зависимости при разных значениях реактивного двигателя (рис. 4-5). 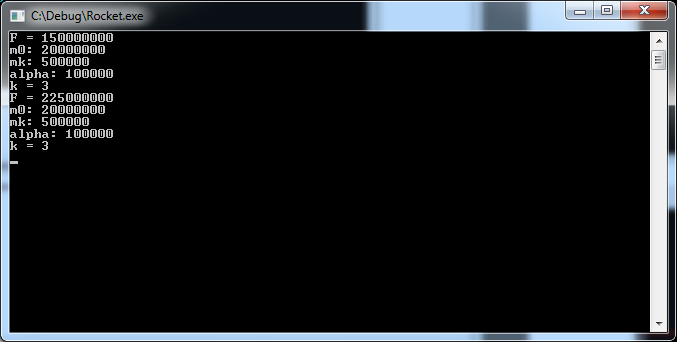 Рис. 4 – Задание параметров 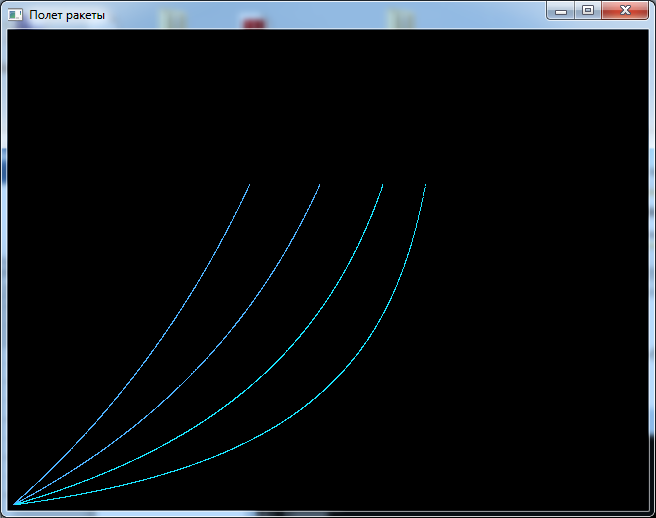 Рис. 5 – Зависимость H(t) Заключение Общее исследование движения ракеты показывает, что конечная скорость ракеты может быть увеличена несколькими способами: путем повышения удельной тяги реактивного двигателя, путем повышения отношения начального веса ракеты с топливом к весу полезного груза, путем снижения веса конструкции. Существует еще и гиперреактивный путь увеличения скоростных показателей - за счет придания процессу изменения массы динамического, т.е. ускорительного характера. Циолковский теоретически исследовалдвижение ракет в космическом пространстве, подробно изучил условия взлета с различных планет, рассмотрел задачи о возвращении с какой-либо планеты или астероида на Землю, выдвинул идею составных ракет (ракетных поездов) для исследования космического пространства и др. Список использованной литературы 1. Е. Пономарев. Опыты для изучения реактивного движения. Лаборатория кванта: http://kvant.mccme.ru/ 2. Сивухин Д.В. Общий курс физики: Учеб. пособие для вузов. В 5 т. Е.1. Механика. – 5-е изд., стереот. – М.:ФИЗМАТЛИТ, 2006. 3. Физика: Механика. 9 кл.: Учеб. для углубленного изучения физики/М.М.Балашов; Под ред. Г.Я.Мякишева. – 3-е изд. – М.:Дрофа, 2001. 4. «Бьерн Страуструп. Язык программирования С++» 5. Джесс Либерти, «Освой самостоятельно C++ за 21 день», изд. Дом «Вильямс», Москва - Санкт-Петербург – Киев, 2001 6. Н. Секунов, «Самоучитель Visual C++ 6», изд. «БХВ-Петербург», Санкт-Петербург, 2003. Приложение Кодинг программы #include "stdafx.h" #include #include #include using namespace std; double ro = 1.29; double g = 9.8; double dt = 0.1; double c = 0.45; double b = 0.00129; double F ; double s = 20; double alpha; double m0 ; double mk ; double m, a, v, h, t, k; //Рисуем траекторию тела брошенного под углом к горизонту с учетом сопротивления среды void render_scene(){ //Очищаем текущим цветом glClear(GL_COLOR_BUFFER_BIT); //Рисуем координатную систему //Задаем цвет рисовки красным glLineWidth(4.0); glColor3d(1.0, 1.0, 1.0); glBegin(GL_LINES); glVertex2d(0.0, 0.0); glVertex2d(1.4, 0.0); glEnd(); glBegin(GL_LINES); glVertex2d(0.0, 0.0); glVertex2d(0.0, 1.4); glEnd(); glLineWidth(1.0); glColor3f(1.0, 0.0, 0.0); float i; for (i = 0; i <= 1.3; i = i + 0.25){ glBegin(GL_LINES); glVertex2f(1.0, i); glVertex2f(1.0, i + 0.1); glEnd(); } for (i = 0; i <= 1.3; i = i + 0.25){ glBegin(GL_LINES); glVertex2f(i,1.0); glVertex2f(i+0.1,1.0); glEnd(); } cout << "F = "; cin >> F; cout << "m0: "; cin >> m0; cout << "mk: "; cin >> mk; cout << "alpha: "; cin >> alpha; cout << "k = "; cin >> k; for (i = 0; i <= k; i = i + 1){ F = F + F*0.5; v = 0; h = 0; t = dt; double tk = ((m0 -mk) / alpha); glColor3d(i/10.0, 1.0 - i/10.0, 1.0); glBegin(GL_POINTS); while ((t <= tk) && (v <= 1.0)){ m = m0 - alpha*t; a = (F - m*g - (1 / 2)*c*ro*exp(-b*h)*s*v*v) / m; v = v + a*dt / 7800; h = h + v*dt; glVertex2d(t / tk, v); t += dt; } glEnd(); glutSwapBuffers();} } void change_size(GLsizei w, GLsizei h) { if (h == 0) h = 1; float ratio = w*1.0 / h; glMatrixMode(GL_PROJECTION); glLoadIdentity(); glViewport(5, 5, w, h); gluOrtho2D(0, 1.5, 0, 1.5); glMatrixMode(GL_MODELVIEW); glLoadIdentity(); } void Initialise(){ //Цвет очистки черный glClearColor(0.0, 0.0, 0.0, 0.0); } int main(int argc, char** argv) { //Создание окна glutInit(&argc, argv); glutInitDisplayMode(GLUT_DOUBLE | GLUT_RGB); glutInitWindowSize(640, 480); glutInitWindowPosition(20, 20); glutCreateWindow("Полет ракеты"); //Вызов обратных функций glutDisplayFunc(render_scene); glutReshapeFunc(change_size); Initialise(); //initMenu(); // Запустить оболочку GLUT glutMainLoop(); return 0; } |