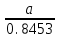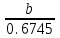1. Исследование модели измеряемого параметра
 Скачать 329.07 Kb.
|
           2 Кременецкая Лит. Дата № докум. Лист Изм. Утв. Н.контр. Пров. Разраб.     1.Исследование модели измеряемого параметра Перед началом работы были изучены общие сведения о спектрах, применяемых в науке и технике. Также параграфы Темы 1 прилагаемого электронного учебного пособия: 1.1. Виды испытаний АТ 1.2. Структура испытаний АТ 1.3. Результаты испытаний АО, как исходные данные для проверки статистических гипотез 1.4. Оценка закона распределения 1.5. Методика построения гистограмм. Дано: исследуется модель измеряемого в вольтах сигнала:  ,где  - неслучайный периодический сигнал;  - случайная помеха с  =0.Требуется: 1. Определить характер и параметры периодического сигнала .2. Определить вид распределения и параметры распределения случайной составляющей .3. Исследовать достоверность оценки вида распределения и параметров распределения от времени наблюдения и количества интервалов статистического ряда. Выбор модели измеряемого параметра построение графика сигнала и его спектра. На рисунке 1 показана реализация выходного сигнала модели: 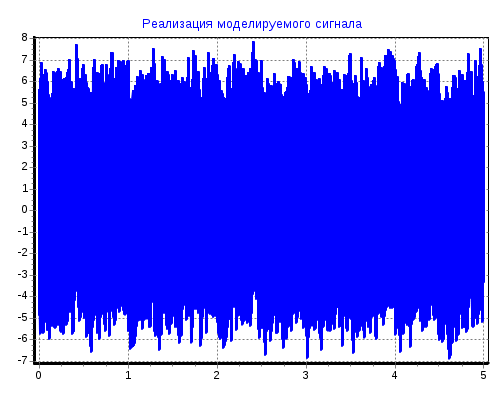. Рисунок 1 – Реализация выходного сигнала модели На рисунке 2 энергетический спектр этой реализации 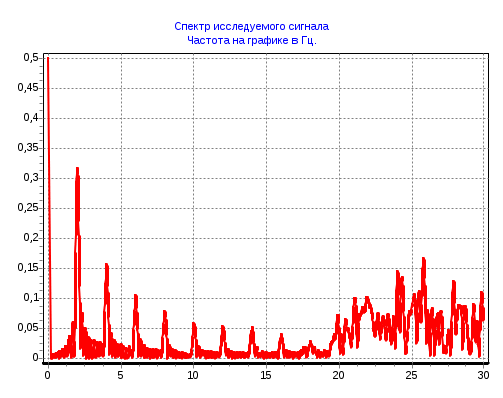 . Рисунок 2 – Спектр исследуемого сигнала. Не меняя исходные данные , повторили эксперимент. Спектры сигнала, полученные при повторном эксперименте представлены на рисунках 3, 4. 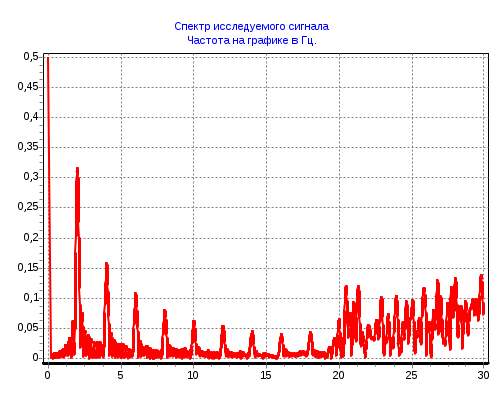 Рисунок 3 – Спектр исследуемого сигнала при повторном эксперименте 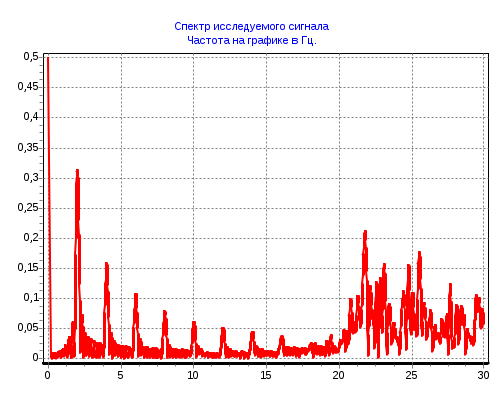 Рисунок 4 – Спектр исследуемого сигнала при повторном эксперименте 1.2. Исследование спектра сигнала. Частотная граница между неслучайной 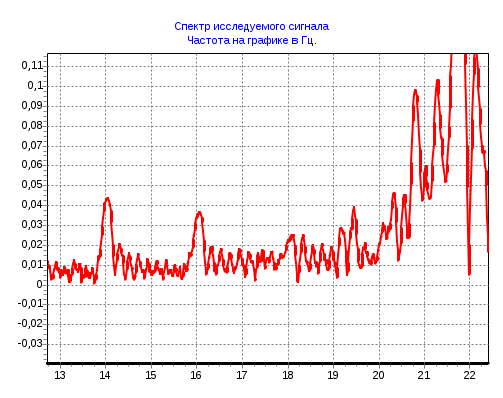 и случайной  составляющими исследуемого сигнала 17 Гц. На рисунке 5 показана гармоника сигнала с частотой 17 Гц и ее боковые лепестки, вызванные малым временем наблюдения (или моделирования) сигнала. Рисунок 5 – Гармоника полезного сигнала с частотой 17 Гц и ее боковые лепестки 1.3 Выделение неслучайной и случайной составляющих сигнала  с помощью цифрового фильтра.По результатам исследования спектра ввели частоту границы, полученную в п.п 1.2. в редактор «F нижн» и нажали кнопку «Построить». Полученные результаты: На рисунке 6 представлена низкочастотная составляющая 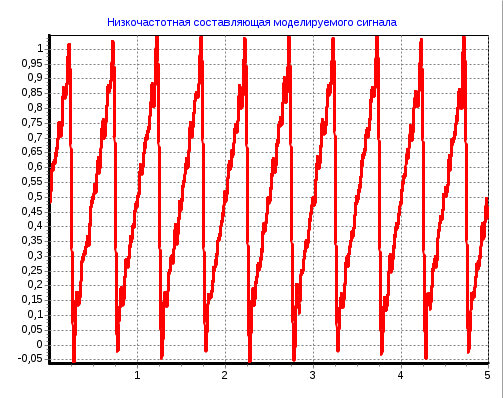моделируемого сигнала . Рисунок 6 – Низкочастотная составляющая моделируемого сигнала На рисунке 7 показана высокочастотная случайная составляющая 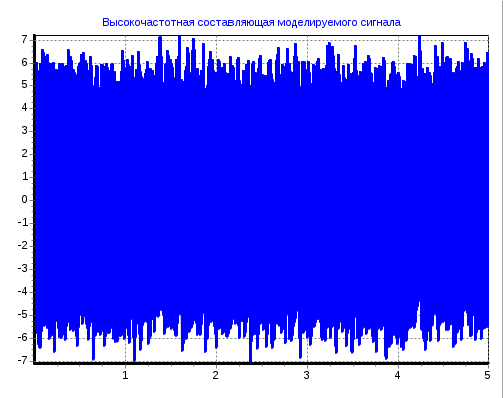. Рисунок 7 – Высокочастотная случайная составляющая На рисунке 8 изображен спектр случайной составляющей 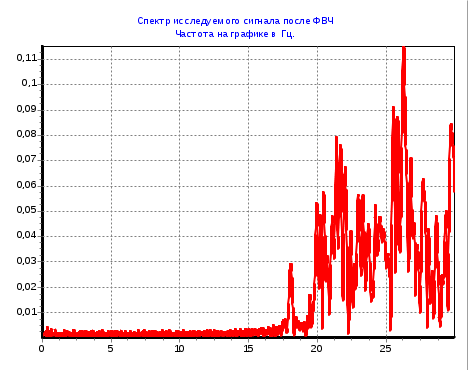. Рисунок 8 –Спектр случайной составляющей .С учетом рисунка 3 (п.п. 1.1 и 1.2) определить по рисунку 6 параметры неслучайного сигнала :- период повторения колебаний равен 0,5с; - амплитуда колебаний – 0,55; - значение постоянной составляющей сигнала – 0,5; - форма сигнала похожа на пилу. По графику представленному на рисунке 7 определили диапазон изменения случайного сигнала равен (-7; 7).На рисунке 8 видно, что спектр сигнала имеет ярко выраженный максимум на частоте 30 Гц, не меняющейся при повторении эксперимента. Частотный диапазон шума составляет от 17 до 40 Гц. 1.4. Построение и исследование гистограммы случайной составляющей .1.4.1. Исследование гистограммы при малом числе интервалов построения гистограммы. Поскольку случайная составляющая сигнала представлена в виде последовательности измерений, то можно построить гистограмму распределения этих измерений. Гистограмма функции плотности распределения случайной составляющей 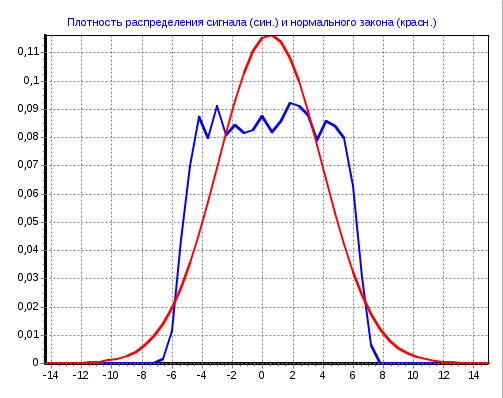показана на рисунке 9. Рисунок 9 – Гистограмма плотности распределения случайной составляющей Гистограмма плотности распределения случайной составляющей показана на рисунке 9 синим цветом. Для сравнения на рисунке 9 красным цветом показана плотность распределения случайной величины  распределенной по нормальному закону с параметрами распределения  и  Параметры распределения случайной составляющей выведены в окнах редакторов под кнопкой «Построить гистограмму». =11,79,  =3,43,  =0,5.При решении задач принятия непараметрических гипотез о статистическом распределении случайных величин применение критерия Пирсона не всегда бывает целесообразно по тем или иным практическим соображением. Если требуется проверить гипотезу о принадлежности статистического распределения исследуемой случайной величины только к нормальному закону распределения, то на практике применим следующий метод. Для любой случайной величины 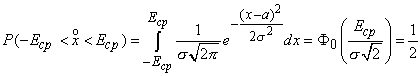 подчиняющейся нормальному закону распределения с центром рассеивания при х=а срединная ошибка определяется выражением Поскольку  при х =0,4769, то .Характеристикой ошибок также является средняя арифметическая ошибка  , равная математическому ожиданию абсолютной величины ошибок. Для нормального закона распределения .Из этого следует, что для нормального закона распределения должны выполняться соотношения:  и  .Если получена статистическая функция распределения для некоторой случайной величины х, то вопрос о том, следует ли считать данную случайную величину подчиняющейся нормальному закону распределения или нет, целесообразно решать так. Пусть имеем значения случайной величины:  Определяем среднее арифметическое значение а  Определяем значения центрированной случайной величины   Абсолютные величины значений  , располагают в ряд в возрастающем порядке. Если  нечетное, то за срединное отклонение или срединную ошибку  принимают ту абсолютную величину  в составленном ряде абсолютных величин, которая занимает  место, если - четное, то за принимают среднее арифметическое абсолютных величин, стоящих на местах с номерами  и  .Составим далее среднюю арифметическую ошибку по формуле  .Определяем среднеквадратическое отклонение  .Далее определяем отношения  и  .Для случайной величины, подчиненной нормальному закону, отношения 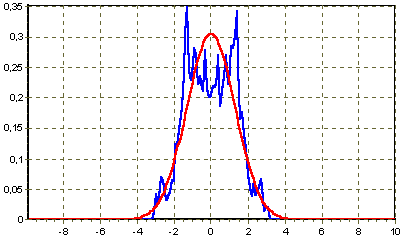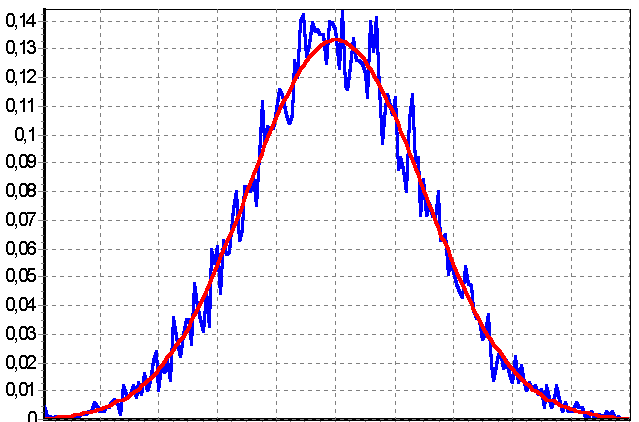и соответственно равны 0,8453 и 0,6745. Если отношения и отличаются от 0,8453 и 0,6745 на величину менее 10%, то условно принимают, что случайная величина подчиняется нормальному закону как показано на рисунке 10   =1,1452 и  =1,217 =0,9941 и =0,9914Рисунок 10 – Проверка непараметрической гипотезы о принадлежности статистического распределения случайной величины к нормальному закону распределения. 1.4.2. Исследование гистограммы при различном числе интервалов построения гистограммы. Три раза выполнить п.п. 1.4.1. задавая число интервалов в соответствии графой 1 таблицы. Каждый раз зарисовывать «График 5» и заполнить таблицу: Таблица 1 – Результаты исследовая гистограммы при различном числе интервалов построения гистограммы
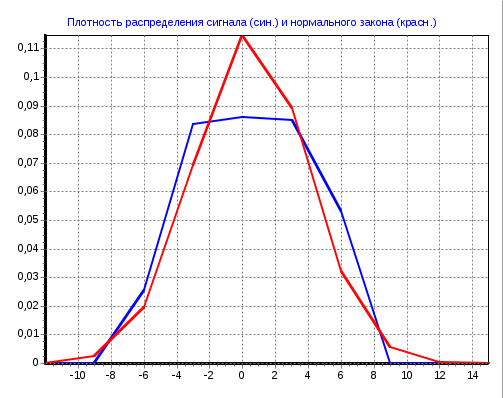 Рисунок 11 – Плотность распределения сигнала (син) и нормального закона (красн) при числе интервалов 10 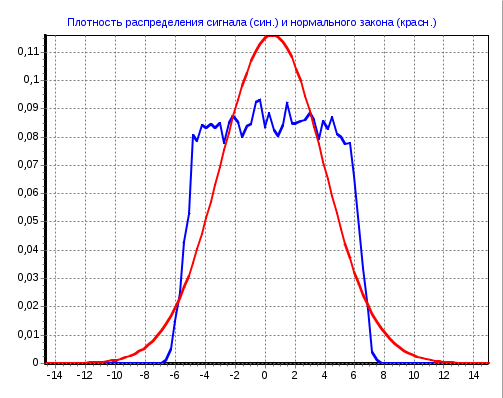 Рисунок 11 – Плотность распределения сигнала (синий) и нормального закона (красный) при числе интервалов 100 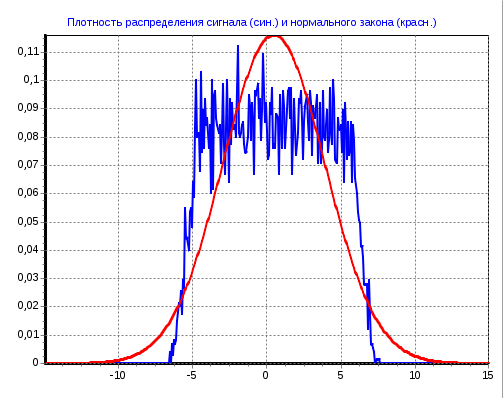 Рисунок 11 Плотность распределения сигнала (синий) и нормального закона (красный) при числе интервалов 400 Вывод: для случайной величины, подчиненной нормальному закону, отношения и соответственно равны 0,8453 и 0,6745. Если отношения и отличаются от 0,8453 и 0,6745 на величину менее 10%, то условно принимают, что случайная величина подчиняется нормальному закону. В нашем случае отношения не отличаются на величину менее 10%, следовательно, случайная величина подчиняется нормальному закону. С увеличением интервалов видно, что гистограмма плотности распределения случайной составляющей  (синяя), изменяется, так же как и красным цветом показана плотность распределения случайной величины  распределенной по нормальному закону с параметрами распределения  и  , равными соответствующим параметрам распределения случайной составляющей , полученным в эксперименте. Оценки параметров распределения  =11,79,  =3,43,  =0.5 случайной составляющей . Сделав вывод об истинности или ложности гипотезы  о нормальном распределении случайной составляющей выяснилось, что все гипотезы ложные.       ИрГУПС Группа ПСм1 −19−1 У Листов Лист ЛР.420300.200100.62.ПЗ Тихий И. И. Подп. |
.
