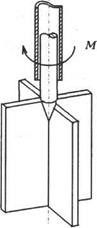
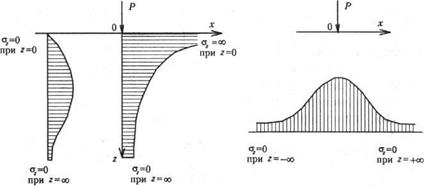
ДОТ. 1. Какие вопросы рассматриваются в механике грунтов

• Название: 1. Какие вопросы рассматриваются в механике грунтов
• Дата: 19.04.2023
• Размер: 379.78 Kb.
• Имя файла: ДОТ.docx
• Тип: Документы; #1073651
• страница: 2 из 5

32. Закон Гука в главных нормальных напряжениях. Сколько независимых характеристик сжимаемости вы знаете?

Закон Гуказаписывается в следующем виде:

 ;

 ;

   .

Поскольку оси х, у и zсовпадают с главными осями, касательные напряжения вдоль них равны нулю, то есть   Независимых характеристик сжима-емости (деформируемости) для изотропного грунта две: 1) модуль общей (упругой и остаточной) деформации- Е₀, МПа и 2) коэффициент Пуассона- µ_0.

33. Что называется коэффициентом Пуассона?

Коэффициентом Пуассона называется отношение относительных деформаций поперечной ε_xк продольной ε_y взятое с обратным знаком, в случае, если действуют только вертикальные напряжения σ_z(напряжения σ_х и σ_у в этом случае отсутствуют).

34.Что называется коэффициентом бокового давления грунта, от чего он зависит и как связан с коэффициентом Пуаасона?

Коэффициентом бокового давления грунта ξ называется отношение приращения бокового давления Δσ_x(илиΔσ_y) к приращениювертикального давления Δσ_z, при обязательном отсутствии боковых деформаций (ε_x=ε_y =0), то есть

 ; ε_x=ε_y =0.

Боковое давление в этом случае является реактивным. Примером может служить грунт, обжимаемый в одометре (компрессионном приборе). Коэффициент бокового давления зависит от вида грунта, его плотности и влажности. С коэффициентом Пуассона он связан следующей зависимостью:



Он изменяется в пределах от 0 до 1.

 

35 Закон Дарси. Какова размерность коэффициента фильтрации? От чего он зависит? Что такое начальный градиент фильтрации?

Закон Дарси записывается так:



то есть, скорость фильтрации грунтовых вод прямо- пропорциональна градиенту напора I и некоторому коэффициенту характеризующему водопроницаемость грунта, т.е.коэффициенту фильтрации к_ф. Коэффициент фильтрации зависит   от вида грунта, размера его пор (то есть от линейного размера пор, но не пористости), от температуры жидкости (меняется ее вязкость).

Начальный градиент фильтрации - величина градиента фильтрации в глинистых грунтах, при котором начинается практически ощутимая фильтрация. Закон Дарси с учётом начального градиента фильтрации выражается следующим образом:

 при 

v_ф = 0 при I ≤ I₀

36. Закон Кулона. Что называется углом внутреннего трения?

Под действием внешней нагрузки в отдельных точках (областях) грунта эффективные напряжения могут превзойти внутренние связи между частицами грунта, при этом возникнут скольжения (сдвиги), и прочность грунта может быть превзойдена.

Внутренним сопротивлением части в песках будет лишь трение, а в глинах (связных грунтах) плюс вязкие, водно-коллоидные связи. Разделить эти сопротивления не представляется возможным.

Закон Кулона (1773г.) имеет следующий вид :




а формулируется: предельное сопротивление грунтов сдвигу прямо пропорционально нормальному давлению.

φ –угол внутреннего трения - параметр линейного графика среза образца грунта;

tgφ-коэффициент внутреннего трения; c- удельное сцепление.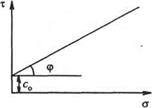

 



Результаты испытания глинистого грунта прямым срезом.

 

37. От чего зависит угол внутреннего трения песка? Что такое угол естественного откоса и совпадает ли он с углом внутреннего трения?

Угол внутреннего трения зависит от крупности и минералогического состава песка, от его пористости и в значительно меньшей степени от влажности

(часто от влажности совсем не зависит). Угол внутреннего трения не совпадает по своей величине с углом естественного откоса, именуемого иногда углом "внешнего трения". Угол естественного откоса влажного песка может быть больше угла внутреннего трения, так как в этом случае действуют капиллярные силы, удерживающие откос от разрушения.

 

38. Чем вызвано сопротивление срезу связного грунта (глинистого грунта)?

Сопротивление срезу связного глинистого грунта характеризуется междучастичными связями - пластичными водно-коллоидными и хрупкими цементационными связями.

 

39. Что такое открытая и закрытая системы испытаний глинистого грунта?

При открытой системе вода имеет возможность под действием передающегося на нее давления выходить из пор грунта наружу, то есть отфильтровываться. При закрытой системе вода не имеет возможности выходить из грунта, то есть вода полностью остается в порах грунта и не перемещается.

40. Что такое полное, эффективное и нейтральное давления? Что называется гидростатическим и поровым давлениями?

Полное давление - это все давление, приходящееся на данную площадку. Эффективное давление - это часть полного давления, воспринимаемая минеральным скелетом грунта.

Нейтральное давление - давление, воспринимаемое водой. Таким образом, эффективное и нейтральное давления составляют полное давление. Гидростатическое и поровое давления составляют в сумме давление в воде, то есть нейтральное давление. Гидростатическое давление - это давление, которое установится в воде, когда полностью исчезнет избыточное по отношению к нему давление, то есть поровое давление.

Эффективным давление на скелет грунта называется потому, что оно повышает сопротивление грунта срезу.

 

41. Каково минимальное число опытов для определения угла внутреннего трения φ и удельного сцепления с?

Поскольку неизвестных две величины, то и минимальное число опытов - два (потом решаются два уравнения с двумя неизвест­ными). Для несвязного грунта, у которого с = 0, минимально воз­можен один опыт, с помощью которого устанавливается величина угла внутреннего трения φ. Это и есть минимальное количество опытов, но исключающее возможность статистической обработки результатов.

 42. Какие методы определения характеристик прочности грунтов в полевых условиях вы знаете?

В полевых условиях в основном распространены следующие методы испытаний: 1) сдвиг штампа, прибетонированного к грунту; 2) срез целика, помещенного в обойму и нагруженного сверху нагрузкой; 3) испытание крыльчаткой; 4) зондирование с помощью конуса.

При сдвиге штампа он обычно прибетонируется к основанию и часть цементного раствора затекает в грунт, обеспечивая контактное сцепление. Сдвиг целика по существу воспроизводит срезной прибор. Нагрузка сверху и сдвигающие усилия создаются домкратами, упирающимися в вертикальный портал и в упорный массив. Об испытании крыльчаткой и зондированием см.вопрос 43.

43. Что такое крыльчатка и какую характеристику прочности можно получить с ее помощью?

Крыльчатка представляет собой две одинаковые прямоугольные взаимно
перпендикулярные, расположенные в вертикальной плоскости пластинки, насаженные на вертикальную ось(см. рис.). К этой оси прикла-
дывается крутящий момент М и измеряется его предельная величина. По
крутящему моменту вычисляется сопротивление сдвигу глинистого грунта τ_s, имея в виду, что τ_s определяется сцеплением грунта (трение не учитывается, поэтому результаты более надежны для грунтов с относительно малым углом внутреннего трения и при малых глубинах испытаний, где давление от собственного веса грунта невелико).

При расчетах принимают обычно, что получаемое по лопастным испытаниям сопротивление сдвигу τ_s приближенно равно общему сцеплению грунта, т.е. τ_s≈ с.

 

44. Принцип линейной деформируемости? Какова зависимость между общими деформациями и напряжениями?

При не очень больших изменениях внешних давлений (1-3кгс/см²), а для плотных и твердых (5-7кгс/см²) с достаточной для практических целей точностью зависимость между деформациями ε и напряжениями σ может приниматься линейной. Это значительно упрощает расчеты и не вносит в них недопустимых погрешностей.Как показано проф. Н.М.Герсевановым (1931), если зависимость между общими деформациями и напряжениями линейна, то для определения напряжений в грунтах полностью будут применимы решения теории упругости.

Изложенное позволяет сформулировать принцип линейной деформируемости:

-при небольших изменениях давлений, грунты можно рассматривать как линейно деформируемые тела.

5. Как вычислить вертикальные напряжения в массиве грунта от его собственного веса и чему они равны?

Вертикальное напряжение от собственного веса грунта σ_z представляет собой вес столба грунта над рассматриваемой точкой с площадью поперечного сечения, равной единице. Таким образом, если в точке на глубине zгрунт однородный по всей глубине, получаем:

σ_z= γz,

Если имеются различные слои, то:

 .

Удельный вес грунта ниже горизонта воды принимается с учетом действия выталкивающей силы за счет взвешивания в воде.

На границе водоупора в эпюре σ_zимеет место скачок на величину Δσ_h=γ_w·h₂.

 

46. Следует ли учитывать деформации грунта от его собственного веса?

Деформации грунта от его собственного веса обычно не учитываются, так как они давно завершились. Однако в том случае, если в силу обстоятельств изменяется структура грунта, то сила собственного веса грунта вызывает в нем дополнительные деформации (например, при увлажнении лессового грунта, из-за которого растворяются жесткие цементационные связи, или оттаиваний вечномерзлого грунта).

 

47. Какие основные положения приняты в теории упругости?

Основные положения теории упругости следующие:

1. Тело является сплошным и изотропным (деформационные свойства в различных направлениях одинаковы).

2. Тело является упругим и со снятием нагрузки все деформации исчезают.

3. Напряжения в теле отсутствуют, если нет внешней нагрузки.

4. Тело является "бесконечно" прочным, то есть в нем не возникает разрушений и трещин, изменяющих напряженное состояние.

5. Связь между напряжениями и деформациями является линейной и описывается законом Гука.

 

48. Какие основные положения приняты в теории линейно-деформируемых тел?

Для того, чтобы можно было воспользоваться решениями задач, имеющимися в теории упругости, приняты следующие положения:

1. Грунт состоит обычно из трех компонентов: минерального скелета, воды и воздуха, однако возможно его рассматривать как квазисплошное тело, то есть тело, имеющее свойства сплошного однородного тела, в котором трещины и пустоты отсутствуют. Грунт можно рассматривать как тело изотропное, обладающее одинаковыми деформационными свойствами в разных направлениях.

2. Для грунта характерно наличие остаточных деформаций. При полном снятии нагрузки все деформации не исчезают, а упругие (то есть восстанавливающиеся) бывают часто значительно меньше неупругих (остаточных) деформаций. Поэтому в теории линейно-деформируемых тел рассматривается только процесс нагрузки, а процесс разгрузки, если в том есть необходимость, рассматривается особо.

3. Считается, что нагрузки на грунт не вызывают его разрушения и далеки от предельных, поэтому в грунтовом массиве не возникает трещин, разрывов, срезов и т.д., то есть не нарушается "квазисплошность".

4. Связь между полными напряжениями и общими деформациями принимается линейной. Таким образом, считается справедливым закон Гука, связывающий напряжения и деформации. Деформации считаются малыми.

 

49. Чем теория линейно-деформируемых тел отличается от теории упругости?

В теории упругости рассматриваются только упругие тела с восстанавливающимися дефор-мациями, а в теории линейно-деформируемых тел рассматриваются общие деформации, включаю-

щие также остаточную деформацию.

 

50. Решение какой задачи теории упругости для полупространства является основным? Чем обусловлена возможность использования её для решения других практически важных задач?

 

Основным является решение задачи о сосредоточенной силе, приложенной к поверх-ности полупространства перпендикулярно к граничной плоскости (задача Буссинеска). Для решения задач о нагрузке, имеющей горизонтальную составляющую, рассматрива-ется дальнейшее развитие решения этой же задачи, но при сосредоточенной силе, действующей вдоль граничной плоскости (как бы "прикрепленной" к ней в одной точке). Аналогичные решения задач о сосредоточенных силах вертикальной и горизонтальной, то есть приложенных перпендикулярно (решение Фламана) и по касательной к границе полуплоскости, также являются основными. Из них путем, интегрирования могут быть получены многие решения интересующих нас в практических целях задач.

51. Действие сосредоточенной силы (основная задача) Какое предположение делается в отношении зоны, расположенной непосредственно у сосредоточенной силы?

Поставленная задача для упругого ( а следовательно, и любого линейно деформи-рованного ) полупространства впервые была полностью решена проф. Ж.. Буссинеском

(1885), а определение напряжений для площадок, параллельных ограничивающей полупространство плоскости,-проф.В.Кирпичевым и проф.Н.А. Цытовичем (1923-1934).

Задача определить напряжения σ_z, τ_zy,τ_zx, как наиболее часто используемых в расчетах.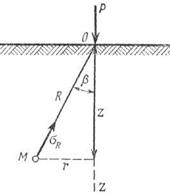

 



Для упрощения расчетов определяют напряжения σ_R в точке М с полярными координатами R и β. Окончательный результат, который полностью совпадает с решением Буссинеска, принимают как постулат, что напряжение σ_Rпропорционально cosβ и обратно пропорционально квадрату расстояния от точки приложения сосредоточенной силы R².

Предполагается, что сплошная среда является бесконечно прочной и не может разрушаться. Ж.Буссинеск, чтобы обойти это обстоятельство, не рассматривал небольшую зону, непосредственно находящуюся у сосредоточенной силы.

Таким образом:   ; для перемещений: 

где:   -коэф .линейно деформируемого полупространства; Е₀ ,μ₀-модули общей и поперечной (аналогичный коэф. Пуассона) деформаций

А- некоторый коэффициент, определяемый из условия равновесия:



Подставляя А в формулу получим:   .

Согласно рис.в вопросе 51 точка М вполне определяется двумя её координатами Zи r. После некоторых преобразований будем иметь:



Для облегчения расчетов служит таблица (Ц. стр79). Величина К определяется для ряда значений r/z.