Контрольная по механике. 1. Колесо радиусом вращается согласно уравнению
 Скачать 145.49 Kb. Скачать 145.49 Kb.
|
|
Вариант 1 1. Колесо радиусом 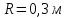 вращается согласно уравнению вращается согласно уравнению 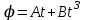 , где , где 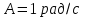 ; ; 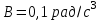 . Определить полное ускорение точек на окружности колеса в момент времени . Определить полное ускорение точек на окружности колеса в момент времени 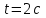 . .2. Двигаясь вверх, кабина лифта массой 800 кг останавливается. Найти ускорение при торможении кабины, если сила натяжения троса кабины 8000 Н, сила трения тормозов 400 Н. 3. Тело массой 3 кг поднимают вертикально с ускорением 4м/с2. При этом совершается работа 126 Дж. На какую высоту подняли тело? 4. Диск радиусом 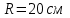 и массой и массой 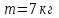 вращается согласно уравнению вращается согласно уравнению 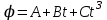 , где , где 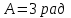 ; ; 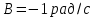 ; ; 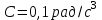 . Найти закон, по которому меняется вращающий момент, действующий на диск. Определить этот момент сил М в момент времени . Найти закон, по которому меняется вращающий момент, действующий на диск. Определить этот момент сил М в момент времени 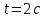 . .Вариант 2 1. Движение материальных точек задано уравнениями 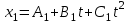 и и 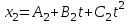 , где , где 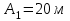 ; ;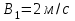 ; ;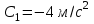 ; ;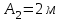 ; ; 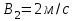 ; ;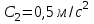 . В какой момент времени скорости этих точек будут одинаковы? Чему равны скорости и ускорения точек в этот момент? . В какой момент времени скорости этих точек будут одинаковы? Чему равны скорости и ускорения точек в этот момент?2. Ускорение кабины лифта в начале движения вниз 0,5м/с2. Найти силу натяжения троса кабины лифта, если масса её 800 кг. Трением пренебречь. 3. К шнуру подвешена гиря. Гирю отвели в сторону так, что шнур принял горизонтальное положение, и отпустили. Масса гири 0,5 кг. Определить силу натяжения в момент прохождения гирей положения равновесия. 4. Маховик радиусом 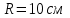 насажен на горизонтальную ось. На обод маховика намотан шнур, к которому привязан груз массой насажен на горизонтальную ось. На обод маховика намотан шнур, к которому привязан груз массой 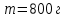 . Опускаясь равноускоренно, груз прошел расстояние . Опускаясь равноускоренно, груз прошел расстояние 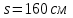 за время за время 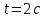 . Определить момент инерции J маховика. . Определить момент инерции J маховика.Вариант 3 Материальная точка движется по окружности радиуса 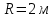 согласно уравнению согласно уравнению 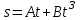 , где , где 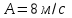 ; ; 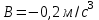 . Найти скорость . Найти скорость 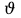 , тангенциальное , тангенциальное 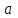 τ , нормальное τ , нормальное 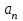 и полное и полное 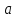 ускорения в момент времени ускорения в момент времени 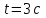 . .2. Автомобиль массой 2т проходит по выпуклому мосту, имеющему радиус кривизны 40 метров, со скоростью 36км/ч. С какой силой автомобиль давит на середину моста. 3. Абсолютно упругий шар массой 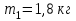 сталкивается с покоящимся упругим шаром большей массы. В результате центрального прямого удара шар потерял 36% своей кинетической энергии. Определить массу m2 большего шара. сталкивается с покоящимся упругим шаром большей массы. В результате центрального прямого удара шар потерял 36% своей кинетической энергии. Определить массу m2 большего шара.4. Через блок радиусом 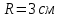 перекинули шнур, к концам которого привязаны грузы массами перекинули шнур, к концам которого привязаны грузы массами 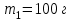 и и 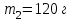 . При этом грузы пришли в движение с ускорением . При этом грузы пришли в движение с ускорением 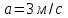 . Определить момент инерции блока. Трение при вращении не учитывать. . Определить момент инерции блока. Трение при вращении не учитывать.Вариант 4 1. Материальная точка движется прямолинейно. Уравнение движения имеет вид 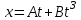 , где , где 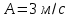 ; ; 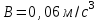 . Найти скорость . Найти скорость 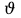 и ускорение точки в моменты времени и ускорение точки в моменты времени 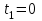 и и 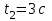 . Каковы средние значения скорости и ускорения за первые . Каковы средние значения скорости и ускорения за первые 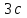 движения? движения?2. Через сколько времени, после начала торможения, остановится автомобиль, если его начальная скорость 15м/с, а коэффициент трения 0,4 определите ускорение автомобиля. 3. Боек свайного молота массой 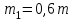 падает с некоторой высоты на сваю массой падает с некоторой высоты на сваю массой 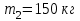 . Найти к. п. д. бойка, считая удар неупругим. Полезной считать энергию, пошедшую на углубление сваи. . Найти к. п. д. бойка, считая удар неупругим. Полезной считать энергию, пошедшую на углубление сваи.4. Тонкий стержень длиной 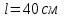 и массой и массой 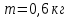 вращается около оси, проходящей через середину стержня перпендикулярно его длине. Уравнение вращения стержня вращается около оси, проходящей через середину стержня перпендикулярно его длине. Уравнение вращения стержня 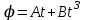 , где , где 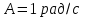 ; ; 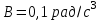 . Определить вращающий момент М в момент времени . Определить вращающий момент М в момент времени 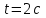 . .Вариант 5 1. Точка движется по прямой согласно уравнению 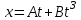 , где , где 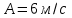 ; ; 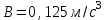 . Определить среднюю скорость . Определить среднюю скорость 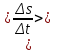 точки в интервале времени от точки в интервале времени от 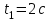 до до 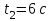 . .2. При движении вниз кабина лифта останавливается тормозами. Найти силу трения в тормозах при ускорении кабины 0,5 м/с2, силе натяжения троса лифта 6000 Н и массе кабины 600 кг. 3. Шарик массой 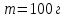 свободно падает с высоты свободно падает с высоты 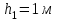 на стальную плиту и подпрыгивает на высоту на стальную плиту и подпрыгивает на высоту 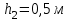 . Определить импульс р (по величине и направлению), сообщенный плитой шарику. . Определить импульс р (по величине и направлению), сообщенный плитой шарику.4. Шарик массой 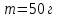 , привязанный к концу нити длиной , привязанный к концу нити длиной 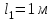 , вращается с частотой , вращается с частотой  , опираясь на горизонтальную плоскость. Нить укорачивается, приближая шарик к оси вращения до расстояния , опираясь на горизонтальную плоскость. Нить укорачивается, приближая шарик к оси вращения до расстояния  . . С какой частотой n2 будет при этом вращаться шарик? Какую работу А совершает внешняя сила, укорачивая нить? Трением шарика о плоскость пренебречь. Вариант 6 1. Две материальные точки движутся согласно уравнениям и  , где , где  ; ; 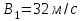 м/с; м/с; 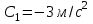 ; ; 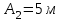 ; ; 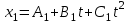 , ,  . В какой момент времени скорости этих точек одинаковы? Чему равны скорости и ускорения точек в этот момент? . В какой момент времени скорости этих точек одинаковы? Чему равны скорости и ускорения точек в этот момент?2. Автомобиль массой 5т движется по вогнутому мосту со скоростью 72км/ч. Мост образует дугу радиусом 100 м. Найдите силу, с которой автомобиль давит на мост, проезжая его середину. 3. Шар массой  движется со скоростью движется со скоростью  и сталкивается с покоящимся шаром массой и сталкивается с покоящимся шаром массой  . Вычислить работу A, совершенную при деформации шаров при прямом центральном ударе. Шары считать неупругими. . Вычислить работу A, совершенную при деформации шаров при прямом центральном ударе. Шары считать неупругими.4. Платформа в виде диска радиусом 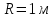 вращается по инерции с частотой вращается по инерции с частотой 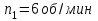 . На краю платформы стоит человек, масса которого . На краю платформы стоит человек, масса которого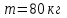 , с какой частотой будет вращаться платформа, если человек перейдет в ее центр? Момент инерции платформы , с какой частотой будет вращаться платформа, если человек перейдет в ее центр? Момент инерции платформы 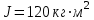 . Момент инерции человека рассчитывать, как для материальной точки. . Момент инерции человека рассчитывать, как для материальной точки.Вариант 7 1. Диск радиусом  вращается согласно уравнению вращается согласно уравнению  , где , где  ; ;  ; ;  . Определить тангенциальное . Определить тангенциальное  , нормальное , нормальное  и полное и полное  ускорения точек на окружности диска для момента времени ускорения точек на окружности диска для момента времени 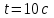 . .2. Тепловоз на горизонтальном участке пути длиной 600м развивает постоянную силу тяги 147 кН. Скорость поезда возрастает от 36 до 54км/ч. Определите силу трения и коэффициент трения, если масса поезда равна 1000т. 3. Атом распадается на две части массами 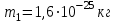 и и 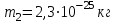 . Определить кинетические энергии Е1и Е2частей атома, если их общая кинетическая энергия Е . Определить кинетические энергии Е1и Е2частей атома, если их общая кинетическая энергия Е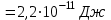 . Кинетической энергией и импульсом атома до распада пренебречь. . Кинетической энергией и импульсом атома до распада пренебречь. 4. Человек стоит на платформе в виде диска и ловит рукой мяч массой 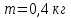 , летящий в горизонтальном направлении со скоростью , летящий в горизонтальном направлении со скоростью 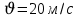 . Траектория мяча проходит на расстоянии . Траектория мяча проходит на расстоянии 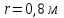 от вертикальной оси вращении. С какой угловой скоростью ω начнет вращаться платформа с человеком, поймавшим мяч? Считать, что суммарный момент инерции человека и платформы от вертикальной оси вращении. С какой угловой скоростью ω начнет вращаться платформа с человеком, поймавшим мяч? Считать, что суммарный момент инерции человека и платформы 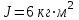 . .Вариант 8 1. По дуге окружности радиуса  вращается точка. В некоторый момент времени нормальное ускорение точки вращается точка. В некоторый момент времени нормальное ускорение точки  , вектор полного ускорения образует в этот момент с вектором нормального ускорения угол , вектор полного ускорения образует в этот момент с вектором нормального ускорения угол  . Найти скорость . Найти скорость  и тангенциальное ускорение и тангенциальное ускорение 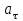 точки. точки.2. Через сколько времени, после начала торможения остановится автомобиль, если его начальная скорость 110 км/ч, если коэффициент трения колес о дорогу µ=0,4 . Определите ускорение а автомобиля. 3. Гиря, положенная на верхний конец спиральной пружины, сжимает ее на 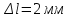 . На сколько сожмет пружину та же гиря, упавшая на конец пружины с высоты . На сколько сожмет пружину та же гиря, упавшая на конец пружины с высоты 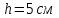 ? ?4. Обруч и диск одинаковой массы катятся без скольжения с одинаковой линейной скоростью. Кинетическая энергия обруча 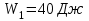 . Найти кинетическую энергию . Найти кинетическую энергию 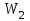 диска. диска.Вариант 9 1. Точка движется по окружности с 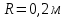 с тангенциальным ускорением с тангенциальным ускорением 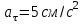 . Через сколько времени после начала движения нормальное ускорение . Через сколько времени после начала движения нормальное ускорение 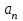 станет вдвое больше тангенциального. станет вдвое больше тангенциального.2. Ускорение кабины лифта в начале движения вниз 0,5м/с2. Найти силу натяжения троса кабины лифта, если масса её 700 кг. Трением пренебречь. 3. Пуля массой  вылетела из ствола автоматического пистолета со скоростью вылетела из ствола автоматического пистолета со скоростью  . Затвор пистолета массой . Затвор пистолета массой  прижимается к стволу пружиной, жесткость которой прижимается к стволу пружиной, жесткость которой  . На какое расстояние отойдет затвор после выстрела? (Считать, что пистолет жестко закреплен.) . На какое расстояние отойдет затвор после выстрела? (Считать, что пистолет жестко закреплен.)4. Сплошной цилиндр скатился с наклонной плоскости высотой 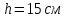 . Определить скорость . Определить скорость 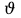 поступательного движения цилиндра в конце наклонной плоскости. поступательного движения цилиндра в конце наклонной плоскости.Вариант 10 1. Колесо вращается так, что зависимость угла поворота колеса от времени дается уравнением 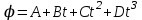 , где , где 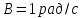 , ,  и и  . Найти радиус колеса, если известно, что к концу второй секунды движения нормальное ускорение точек, лежащих на ободе колеса, равно . Найти радиус колеса, если известно, что к концу второй секунды движения нормальное ускорение точек, лежащих на ободе колеса, равно  . .2. Автомобиль массой 1,5 т, начал разгонятся с постоянным ускорением. Определите скорость автомобиля через 5 секунд, если коэффициент трения µ=0,3, а сила тяги мотора равна 300 Н. 3. Две пружины жесткостью  и и  скреплены последовательно. Определить работу по растяжению обеих пружин, если вторая пружина была растянута на скреплены последовательно. Определить работу по растяжению обеих пружин, если вторая пружина была растянута на  . .4. Сплошной однородный диск катится по горизонтальной плоскости со скоростью  . Какое расстояние пройдет диск до остановки, если его предоставить самому себе? Коэффициент трения при движении диска равен 0,02. . Какое расстояние пройдет диск до остановки, если его предоставить самому себе? Коэффициент трения при движении диска равен 0,02. |
