1. Метод проекций. Виды проецирования 1 Даны изображения фигуры abc
 Скачать 1.73 Mb.
|
|
1. Метод проекций. Виды проецирования 1.1 Даны изображения фигуры ABC: 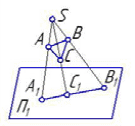   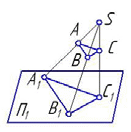 1. 2. 3. 4.
1.2 Прямая при прямоугольном проецировании проецируется в точку при условии... 1. если эта прямая проходит через центр проецирования 2. параллельности этой прямой плоскости проекций 3. если эта прямая находится под углом 45° к плоскости проекций 4. перпендикулярности этой прямой плоскости проекций 1.3 Прямая при центральном проецировании проецируется в точку при условии... 1. если эта прямая находится под углом 45° к плоскости проекций 2. перпендикулярности этой прямой плоскости проекций 3. если эта прямая проходит через центр проецирования 4. параллельности этой прямой плоскости проекций 1.4 Проецирование называют центральным, если проецирующие лучи … 1. проходят через одну точку 2. не параллельны между собой 3. проходят под острым углом к плоскости проекций 4. перпендикулярны плоскости проекций 1.5 Проецирование называют ортогональным, если проецирующие лучи … 1. проходят через одну точку 2. не параллельны между собой 3. проходят под острым углом к плоскости проекций 4. перпендикулярны плоскости проекций 1.6 Плоскость проекций, обозначаемая на чертеже П с соответствующим индексом, называется…
1.7 Проецирование называют ортогональным, если проецирующие лучи … 1. проходят через одну точку 2. параллельны между собой и перпендикулярны по отношению к плоскости проекций 3. параллельны между собой 1.8 Центральное проецирование представлено на изображении: 1, 2, 3 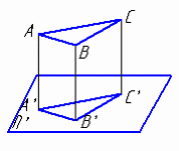 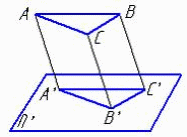 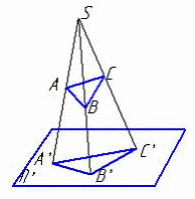 1 2 3 1.9 При центральном проецировании сохраняется… 1. натуральная величина отрезка прямой 2. перпендикулярность отрезков прямых 3. принадлежность точки прямой 4. параллельность отрезков прямых 2. Проецирование точки 2.1 Плоскость, на которой получают изображение геометрического объекта, называют... 1. плоскостью изображений 2. плоскостью проекций 3. плоскостью отображений 4. плоскостью чертежа 2.2 Положение точки на чертеже однозначно определяется как минимум … проекциями. 1. четырьмя 2. пятью 3. двумя 4. тремя 2.3 Проекция точки определяется соответствующими координатами X, Y, Z…
2.4 Даны проекции точек: 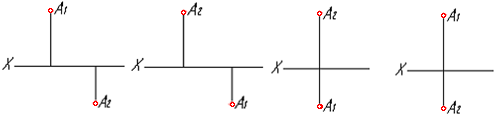 . 1 2. 3. 4.
2.5 Даны проекции точек: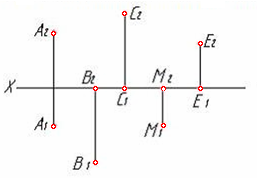 
2.6 Проекция точки на соответствующую плоскость проекций называется…
2.7 Линия, соединяющая на чертеже проекции точки и перпендикулярная к оси проекций, называется… 1. линией проекционной связи 2. линией уровня 3. постоянной чертежа 4. связующей прямой 2.8 Из заданных точек: D (6,5,5); B (12,6,12); A (12,15,15); E (18,17,18); C (9,9,4) 1. От фронтальной и профильной плоскостей проекций равно удалена точка C 2. От профильной плоскости проекций равно удалены точки A,B 3. От горизонтальной плоскости проекций больше всех удалена точка E 4. Ближе всех к профильной плоскости проекций точка D 5. От фронтальной и горизонтальной плоскостей проекций равно удалена точка A 6. От горизонтальной и профильной плоскостей проекций равно удалена точка B 7. Самая низкая точка C 8. Самая высокая точка E 3. Чертеж прямой линии, чертеж плоскости 3.1 Даны чертежи отрезков прямой:  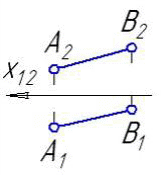 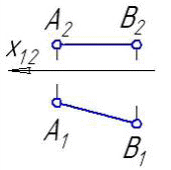  1. 2. 3. 4.
3.2 Плоскость на чертеже можно задать... 1. проекциями скрещивающихся прямых 2. проекциями пересекающихся прямых 3. проекциями треугольника 4. проекциями параллельных прямых 3.3 Минимальное количество геометрических объектов для задания плоскости: 1. две пересекающиеся прямые 2. пять прямых 3. три точки не лежащие на одной прямой 4. одна прямая 3.4 Существует … способа (ов) задания плоскости на комплексном чертеже. 1. три 2. четыре 3. один 4. пять 5. два 6. шесть 3.5 Даны чертежи прямых и плоскостей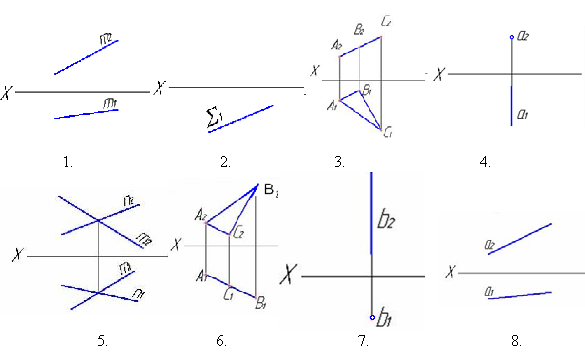 
3.6 Плоскость однозначно задают: 1. две пересекающиеся прямые 2. 3 точки, не лежащие на одной прямой 3. 4 точки 4. 5 точек 3.7 Д  ан чертеж… 1. горизонтальной прямой уровня l 2. профильно-проецирующей прямой l 3. прямой общего положения l 4. фронтальной прямой уровня l 5. горизонтально-проецирующей прямой l 3.8 Геометрические фигуры частного положения расположены относительно плоскостей проекций … 1. под одинаковыми углами наклона 2. перпендикулярно или параллельно 3. не перпендикулярно или не параллельно 4. под разными углами наклона 3.9 Даны чертежи прямых   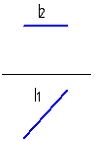  1. 2. 3. 4
3.10 Плоскость на чертеже не задают… 1. точка и прямая 2. три точки 3. две пересекающиеся прямые 4. две параллельные прямые 5. две скрещивающиеся прямые 3.11 Даны чертежи прямых b, d,t,f ,и h. 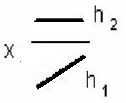 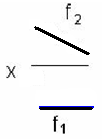 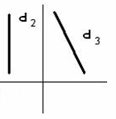 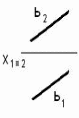 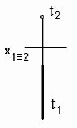 1. 2. 3. 4. 5.
3.12 Отрезок прямой АВ, если А(10,10,30) и В(10,10,50), расположен в пространстве… 1. перпендикулярно профильной плоскости проекций 2. перпендикулярно горизонтальной плоскости проекций 3. параллельно биссекторной плоскости 4. параллельно горизонтальной плоскости проекций 4. Чертеж многогранника. Чертеж поверхности вращения. 4.1 Видимость ребер призмы на П2 верно изображена на чертеже: 1,2, 3, 4   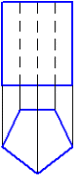 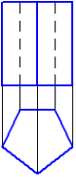 1. 2 . 3. 4. 4.2 Видимость ребер пирамиды на П1 верно изображена на чертеже: 1, 2, 3, 4    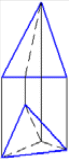 1. 2. 3. 4. 4.3 Даны чертежи поверхностей  1. 2. 3. 4. 5.
4.4 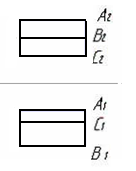 Дан чертеж … 1. пирамиды трехгранной 2. плоскости 3. призмы трехгранной 4. цилиндра 5.призмы четырехгранной 4.5 Даны чертежи поверхностей: 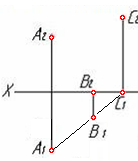 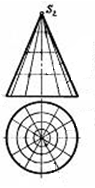 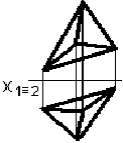 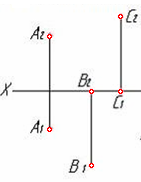 1. 2. 3. 4. 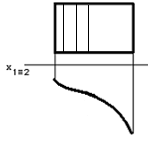 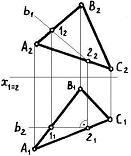  5. 6. 7.
4.6 Даны композиции из геометрических фигур: 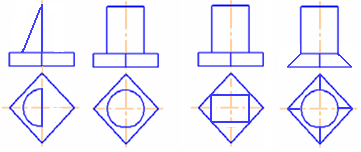 пирамиды и цилиндра -4 конуса и призмы- 1 цилиндра и призмы - 2 двух призм - 3 1 2 3 4 4 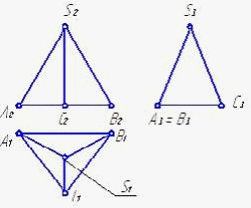 . 7 Грань SAB данной пирамиды - 1 Грань ABС данной пирамиды - 4 Грань SAС данной пирамиды - 3 1. перпендикулярна профильной плоскости проекций 2. принадлежит фронтальной плоскости проекций 3. является плоскостью общего положения 4. параллельна горизонтальной плоскости проекций ПОЗИЦИОННЫЕ ЗАДАЧИ 5. Параллельность на чертеже 5.1 Параллельные прямые aи bизображены на чертеже: 1, 2, 3, 4 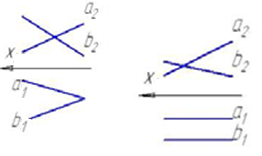 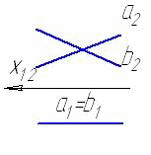  1. 2. 3. 4. 5.2  Плоскости Σ(m║n) параллельна плоскость: 1, 2, 3, 4 1. ∆(b ∩ l) 2. ∆(a ∩ c) 3. ∆(a ∩ b) 4. ∆(c ∩ b) 5. 3 Плоскость Σ(d ∩e)параллельна: плоскости G(ABC) на чертеже 1 плоскости Q(a∩b) на чертеже 2 плоскости R(ABC) на чертеже 3 п  лоскости ∆(a║b) на чертеже 4. 5.4 Прямая m параллельна плоскости Σ(АВС) на чертеже: 1, 2, 3 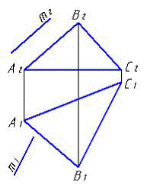 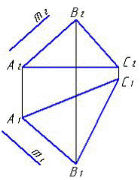 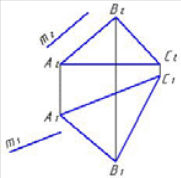 1. 2. 3. 5.5 Прямая m параллельна прямой в плоскости Σ(АВС) на чертеже: 1, 2, 3, 4 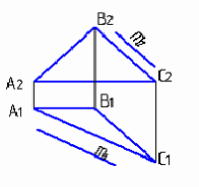 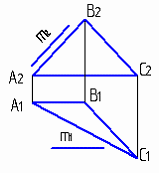 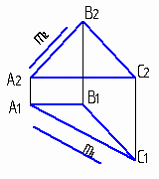 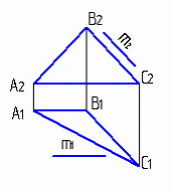 1 2 3 4 5.7 Прямая m не параллельна плоскости Q(АВС) на чертеже: 1, 2, 3, 4 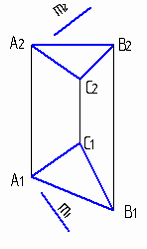 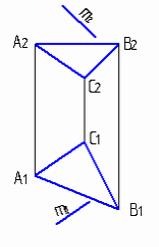 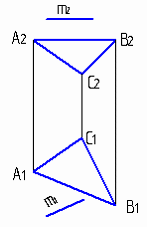 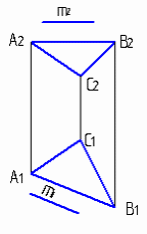 1. 2. 3. 4. 6. Принадлежность точки и линии плоскости и поверхности 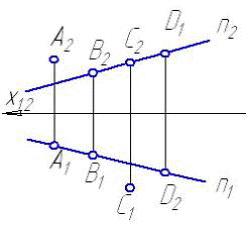 6.1 Прямой n принадлежит точка: A,B, C, D 6 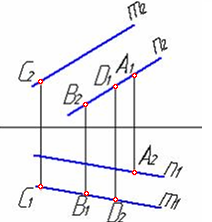 .2Плоскости Σ(m║n) принадлежит точка: A, B, C, D 6.3 Прямой t принадлежит точка … 1 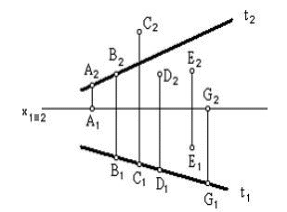 . G 2. А 3. D 4. E 5. С 6. В 6.4 На комплексном чертеже прямая принадлежит плоскости, если проекции … принадлежат соответствующим проекциям прямых, принадлежащих этой плоскости 1. трех её точек 2. одной её точки 3 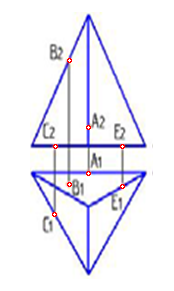 . четырех её точек 4. двух её точек 6.5 Поверхности пирамиды принадлежит точка: A, B, C, E 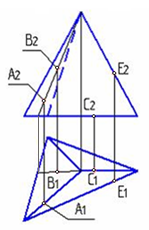 6.6 Поверхности пирамиды не принадлежат точки: A, B, C, E 6 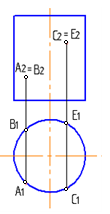 .7 Видимыми на фронтальной проекции цилиндра являются точки… 1. С и А 2. В и Е 3. А и В 4. В и С 6.8 Точка А принадлежит поверхности конуса на чертеже: 1, 2, 3, 4 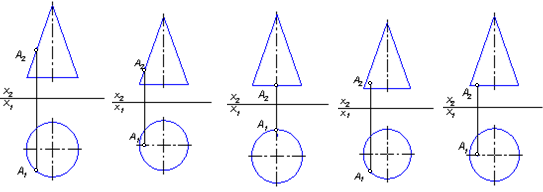 1. 2. 3. 4. 5. 6 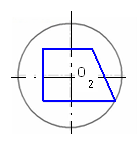 .9 На поверхности сферы дана линия. Горизонтальная проекция этой сферы дана на чертеже: 1, 2, 3, 4, 5  1. 2. 3. 4. 5. 6  .10 Плоскости Σ(m║n) принадлежат точки:1. А и С 2. А и В 3. В и Е 4. А и Е  6 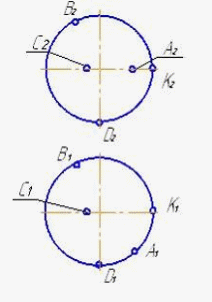 .11 Поверхности сферы принадлежат точки: 1. А и К 2. С и В 3. К и С 4. В и D 7. Пересечение прямой с плоскостью, поверхностью, пересечение двух плоскостей 7.1 Прямую общего положения можно заключить в плоскость… 1. уровня 2. общего положения 3. проецирующую 7.2 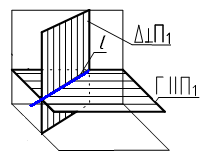 Горизонтальную прямую можно заключить в плоскость частного положения -… 1. горизонтальную плоскость уровня 2. горизонтально-проецирующую плоскость 4. фронтально-проецирующую плоскость 5. фронтальную плоскость уровня 7.3 Точка пересечения К прямой m с плоскостью, заданной треугольником, правильно определена на чертеже: 1, 2, 3, 4 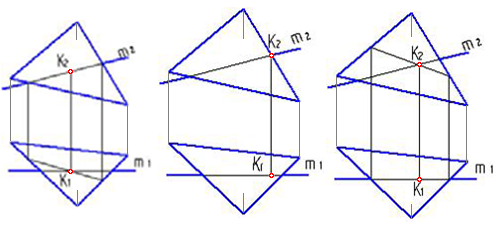 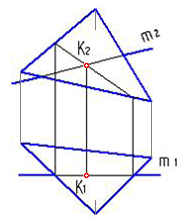 1. 2. 3. 4. 7.4 Точка пересечения K прямой lс плоскостью Σ(m∩n) правильно определена на чертеже: 1, 2, 3, 4 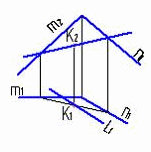    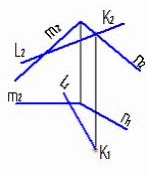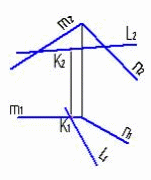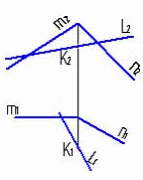1. 2. 3. 4. 7  .5 Для определения точки пересечения К прямой l и плоскости общего положения Σ необходимо... 1. использовать способ сфер 2. определить ее как точку пересечения проекций заданной прямой с проекцией одной из линий, задающих плоскость 3. использовать одну вспомогательную плоскость 4. использовать две вспомогательные плоскости 7 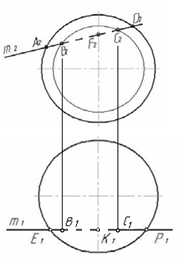 .6Прямая m пересекается с поверхностью сферы в точках: 1. А и D 2. F и D 3. B и C 4. E и P 5. F и K 7.7 Для решения задач на пересечение прямой общего положения и плоскости общего положения применяется вспомогательная … 1. плоскость общего положения 2. прямая частного положения 3. плоскость уровня 4. проецирующая плоскость 7  .8 Для решения задач на пересечение плоскостей общего положения применяется: 1. одна плоскость общего положения 2. одна плоскость частного положения 3. две плоскости частного положения – плоскости уровня 4. проецирующая плоскость 7.9  Две горизонтально-проецирующие плоскости ∆ и ∆ пересе- каются … 1. по прямой общего положения 2. по горизонтальной прямой 3. по горизонтально-проецирующей прямой 4. по фронтально-проецирующей прямой 7  .10Горизонтально-проецирующая плоскость∆ и фронтально-проецирующая плоскость Q пересекаются… 1. по прямой общего положения 2. по горизонтальной прямой 3. по горизонтально-проецирующей прямой 4. по фронтально-проецирующей прямой 7.11 Линия пересечения плоскости, заданной треугольником, и плоскости Σ(m║n), правильно определена на чертеже: 1, 2, 3, 4 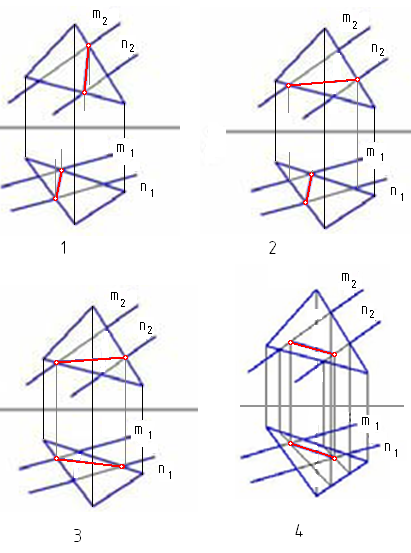 7.12 Г 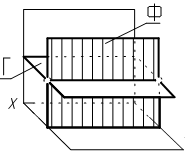 оризонтальная Г и фронтальная Ф плоскости уровня пересекаются…1. по прямой общего положения 2. по горизонтальной прямой 3. по горизонтально-проецирующей прямой 4. по фронтально-проецирующей прямой 5. по профильно-проецирующей прямой |