математика. матем. 1. Найдите сумму всех целых решений неравенства
 Скачать 22.62 Kb. Скачать 22.62 Kb.
|
|
1. Найдите сумму всех целых решений неравенства 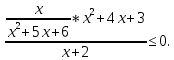 Решение:  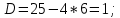 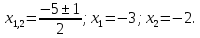      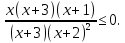 Корни числителя: 0, -3, -1. Корни знаменателя: -3, -2 (четное).  Целые решения неравенства: -1, 0. Их сумма равна -1. Ответ: -1. 2. Число единиц двухзначного числа больше числа десятков на 2, а произведение этого числа на сумму его цифр равна 280. Найти это число. Пусть x – это число десятков, значит, число единиц равно x+2. Искомое число равно  Произведение этого числа на сумму его цифр равна 280: 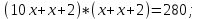  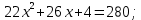 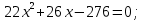 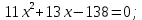  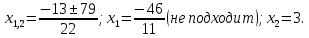 Число десятков равно 3, число единиц равно 5, следовательно, искомое число равно 35. Ответ: 35. 3. Найти среднее арифметическое корней уравнения  Рассмотрим три случая. 1)  исходное уравнение имеет вид: исходное уравнение имеет вид: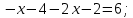  Решений нет, т.к. по условию 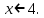 2)  исходное уравнение имеет вид: исходное уравнение имеет вид: 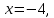  3)  исходное уравнение имеет вид: исходное уравнение имеет вид:  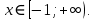 Значит, корни уравнения равны -4, 0. Среднее арифметическое корней уравнения: 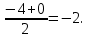 Ответ: -2. 4. Найти сумму целых решений неравенства 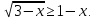 1) Если  , неравенство выполнится при всех допустимых , неравенство выполнится при всех допустимых 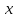 , ведь корень неотрицателен, значит, он автоматически больше (или равен) неположительного числа: , ведь корень неотрицателен, значит, он автоматически больше (или равен) неположительного числа: 2) 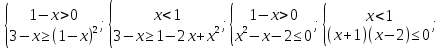 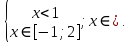 Значит, решение неравенства: 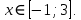 Сумма целых решений неравенства:  Ответ: 5. |
