Работа. Мат. анализ ч.2. 1 Найти точку экстремума функции Лагрнажа из условия равенства нулю ее частных производных 2

• Название: 1 Найти точку экстремума функции Лагрнажа из условия равенства нулю ее частных производных 2
• Анкор: Работа
• Дата: 28.03.2021
• Размер: 406.68 Kb.
• Имя файла: Мат. анализ ч.2.docx
• Тип: Документы; #188791
• страница: 2 из 3

Найти частную производную второго порядка функции z(x,y) по переменной x

		4
		2
		1 верно

Вычислить значение частной производной функции z(x,y) по переменной x в точке (0,0)

		2
		3
		1 верно
		4

Найти частную производную функции z(x,y) по переменной y в точке (0,0)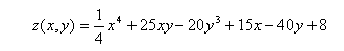




Определить критические точки функции z(x,y)

		1
		3
		4
		2

Укажите верное решение дифференциального уравнения

		4
		1 не совпадает с приведенными ответами
		2
		3

Установите соответствие между дифференциальным уравнением и общим видом его частного решения.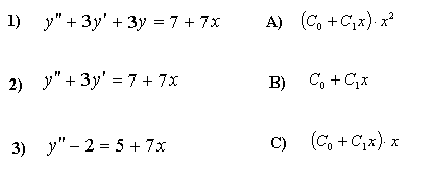

Частное решение третьего дифференциального уравнения
Частное решение первого дифференциального уравнения
Частное решение второго дифференциального уравнения

Вычислить значение несобственного интеграла

		2
		4
		3 верно
		1

Укажите верное значение интеграла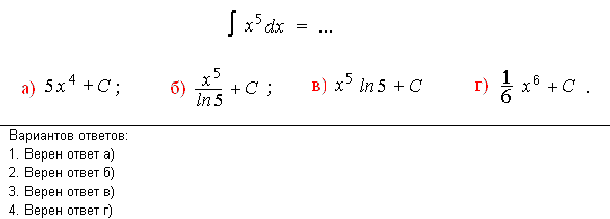

		2
		4 верно
		1
		3

Найти частную производную функции z(x,y) по переменной x в точке (0,0)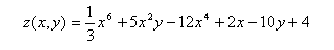



Конец формы

Жанна

Метод множителей Лагранжа используется для

		3
		4
		2
		1 верно

Вычислить значение определенного интеграла



Производная от первообразной для данной функции равна

		4
		2
		3
		1

Вычислить значение частной производной функции z(x,y) по переменной y в точке (0,0)

		4
		3 верно
		1
		2

Найти частную производную функции z(x,y) по переменной y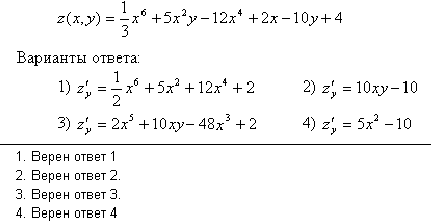

		2
		4 верно
		3
		1

Первообразная для функции f(x)

		3 не очень уверена
		4
		2
		1

Укажите отличие двух различных первообразных одной и той же функции

		4
		1
		2 не уверена
		3

Найти частную производную второго порядка функции z(x,y) по переменной x в точке (1,1)



Найти частную производную функции z(x,y) по переменной x в точке (0,0)



по переменной Y в точке (0,0) = 16, по переменной X = 4X / X^2 + 8Y + 1

Вычислить значение определенного интеграла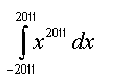





Среди перечисленных ниже выражений укажите правильное для следующего интеграла

		3
		4
		2 ВЕРНО
		1

Укажите верное решение дифференциального уравнения.

		3 ВЕРНО
		2
		4
		1

Предел интегральной суммы на отрезке [a,b],если максимальная длина интервала разбиения стремится к нулю равен

		3
		4
		2
		1