1. Понятие неопределенного интеграла
 Скачать 2.42 Mb. Скачать 2.42 Mb.
|
|
1.Понятие неопределенного интеграла Функция F(х) называется nервообразной. функции f(x) на интервале (а; Ь), если для любого х Е (а; Ь) выполняется равенство F'(х) = f(x) (или dF(x) = f(x) dx). Множество всех первообразных функций F(x) + С для f(x) называется неопределенным интегралом от функции f(x) и обозначается символом ᶘ f(x) dx. Таким образом, по определению ᶘ f(x)dx = F(x) +c 2.Свойства неопределенного интеграла 1 - Дифференциал от неопределенного интеграла равен подынтегральному выражению, а производная неопределенного интеграла равна подынтегральной функции: d(ᶘ f(x) dx) = f(x) dx 2 - Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной: ᶘ dF(x) = Р(х) + С. 3 - Постоянный множитель можно выносить за знак интеграла: ᶘaf(x) dx= а· ᶘf(x) dx, (a не равна нулю) 4 - Неопределенный интеграл от алгебраической суммы конечного числа непрерывных функций равен алгебраической сумме интегралов от слагаемых функций: ᶘ (f(х) ± g(x)) dx = ᶘf(x) dx ± ᶘg(x) dx. 5. (Инвариантность формулы интегрирования). Если ᶘ f(x) dx = F(x) + с, то и ᶘ f(u) du = F(u) + с, где u = y(х) – произвольнаяфункция, имеющая непрерывную производную. 3.Метод интегрирования по частям Пусть u = u(х) и v = v(x) - функции, имеющие непрерывные производные. Тогда d(uv) = ud(v) + vd(u). Интегрируя это равенство, получим ᶘd(uv)= ᶘud(v)+ ᶘvd(u) 4.Интегрирование рациональных дробей 1. Если дробь неправильна, то представить· ее в виде суммы многочлена и правильной дроби; 2. Разложив знаменатель правильной рациональной дроби на множители, представить ее в виде суммы простейших рациональных дробей; 3. Проинтегрировать многочлен и полученную сумму простейших дробей. Рассмотрим интеграл Выделив в знаменателе полный квадрат, получим: 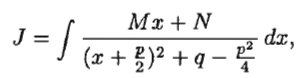 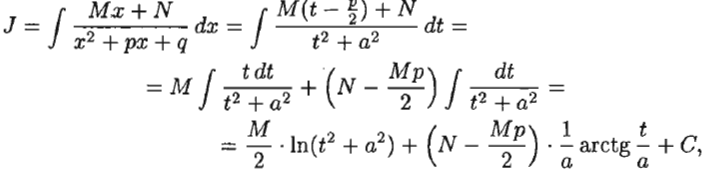 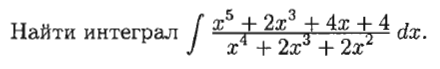 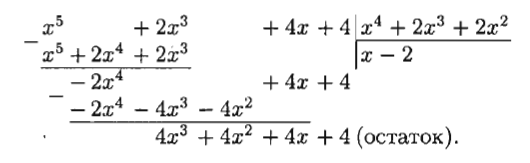 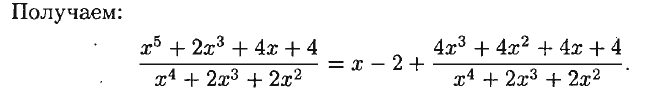 5.ИНТЕГРИРОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ    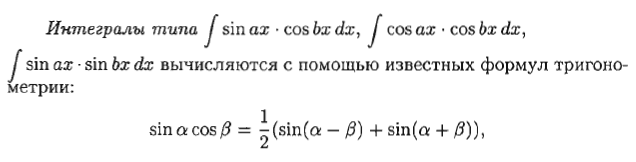 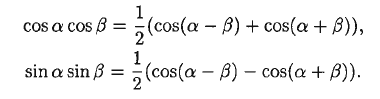 6.ИНТЕГРИРОВАНИЕ ИРРАЦИОНАЛЬНЫХ ФУНКЦИЙ    7. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ КАК ПРЕДЕЛ ИНТЕГРАЛЬНОЙ СУММЫ 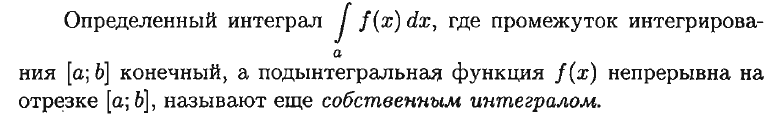   8.ГЕОМЕТРИЧЕСКИЙ И ФИЗИЧЕСКИЙ СМЫСЛ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА   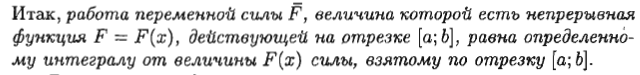  9. ФОРМУЛА. НЬЮТОНА-ЛЕЙБНИЦА Пусть функция у = f(x) интегрируема на отрезке [а; Ь].     10.СВОЙСТВА ОПРЕДЕЛЕННОГО ИНТЕГРАЛА Рассмотрим основные свойства определенного интеграла, считая подынтегральную функцию интегрируемой на отрезке [а; b]. При выводе свойств будем использовать определение интеграла и формулу Ньютона-Лейбница. 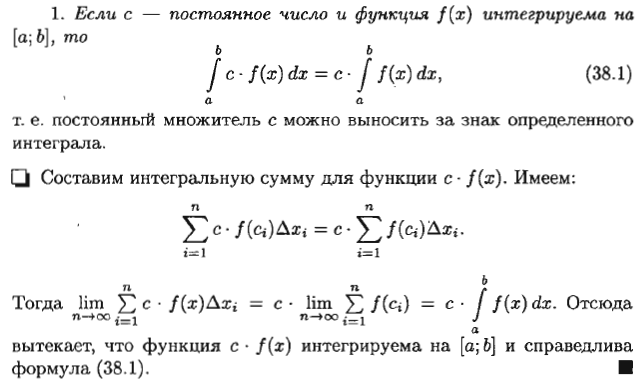   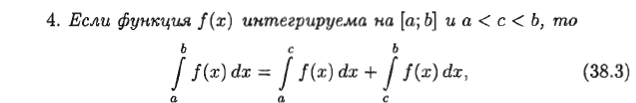   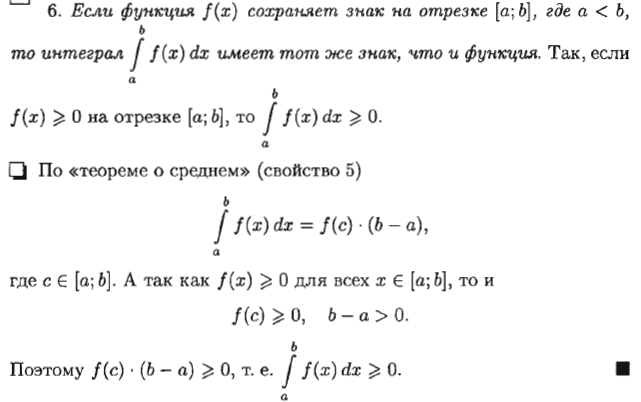      11.НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ  (несобственный интеграл I рода)     (несобственный интеграл 2 рода)  12. Необходимый признак СХОДИМОСТИ ЧИСЛОВОГО ряда.    13.Гармонический ряд    14.Признаки сравнения Рядов   15. Признак Даламбера,  16. Радикальный Признак Коши  17. Интегральный призрак Коши  18.Признак Лейбница  19. Абсолютная И условная СХОДИМОСТИ числовых Рядов.  20.Интервал и радиус сходимости степенного Ряда    21.РЯДЫ Тейлора и Маклорена   |
