Реферат по предмету. Реферат1Вельк. Уравнения дифференциала
 Скачать 146.16 Kb. Скачать 146.16 Kb.
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ КЫРГЫЗСКОЙ РЕСПУБЛИКИ  И. Абдраимов атындагы кыргыз авиацыалык институту Кыргызский авиационный институт им. И. Абдраимова Kyrgyz Aviation Institute named after I. Abdraimov Кафедра естественно-научных дисциплин СРС По предмету: Математика На тему: Уравнения дифференциала Выполнил: Вельк Артём Студент группы: ЭТМо-2-21 Проверила: к.ф-м.н., доц. Нарматова М. Ж. Бишкек 2022 Содержание Введение Основная часть Заключение Список использованных источников Приложения 1. Введение Дифференциалом функции в некоторой точке x называется главная, линейная часть приращения функции. Многие физические законы, которым подчиняются те или иные явления, записываются в виде математического уравнения, выражающего определенную зависимость между какими-то величинами. Часто речь идет о соотношении между величинами, изменяющимися с течением времени, например экономичность двигателя, измеряемая расстоянием, которое автомашина может проехать на одном литре горючего, зависит от скорости движения автомашины. Соответствующее уравнение содержит одну или несколько функций и их производных и называется дифференциальным уравнением. Исследование поведения различных систем (технические, экономические, экологические и др. часто приводит к анализу и решению уравнений, включающих как параметры системы, так и скорости их изменения, аналитическим выражением которых являются производные. Такие уравнения, содержащие производные, называются дифференциальными. Это уравнение, которое помимо функции содержит её производные. Порядок входящих в уравнение производных может быть различен (формально он ничем не ограничен). Производные, функции, независимые переменные и параметры могут входить в уравнение в различных комбинациях или отсутствовать вовсе, кроме хотя бы одной производной. В отличие от алгебраических уравнений, в результате решения которых ищется число (несколько чисел), при решении дифференциальных уравнений ищется функция или семейство функций. Первоначально дифференциальные уравнения возникли из задач механики, в которых требовалось определить координаты тел, их скорости и ускорения, рассматриваемые как функции времени при различных воздействиях. К дифференциальным уравнениям приводили также некоторые рассмотренные в то время геометрические задачи. Основой теории дифференциальных уравнений стало дифференциальное исчисление, созданное Лейбницем и Ньютоном (1642—1727). Сам термин «дифференциальное уравнение» был предложен в 1676 году Лейбницем. 2. Основная часть Уравнение в полных дифференциалах - этот тип, вследствие того, что к нему сводятся многие другие уравнения, имеет важное значение в теории дифференциальных уравнений. Речь идет об уравнении в полных дифференциалах. Так называется уравнение левая часть которого представляет собой полный дифференциал некоторой функции Относительно функций Пример. Решить дифференциальное уравнение Проверим, что данное уравнение является уравнением в полных дифференциалах: 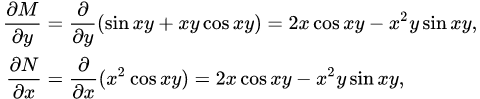 так что так что При решении различных задач математики, физики, химии и других наук часто пользуются математическими моделями в виде уравнений, связывающих независимую переменную, искомую функцию и ее производные. Такие уравнения называются дифференциальными термин принадлежит Г. Лейбницу, 1676 г. Решением дифференциального уравнения называется функция, которая при подстановке в уравнение обращает его в тождество. Так, решением уравнения у = f(x) является функция у = F(x) первообразная для функции f(x). Рассмотрим некоторые общие сведения о дифференциальных уравнениях (ДУ). Если искомая (неизвестная) функция зависит от одной переменной, то ДУ называют обыкновенным; в противном случае - ДУ в частных производных. Наивысший порядок производной, входящей в ДУ, называется порядком этого уравнения. Процесс отыскания решения ДУ называется его интегрированием, а график решения ДУ интегральной кривой. Если дифференциальное уравнение является многочленом относительно старшей производной, то степень этого многочлена называется степенью дифференциального уравнения. Если дифференциальное уравнение является многочленом относительно старшей производной, то степень этого многочлена называется степенью дифференциального уравнения. Все дифференциальные уравнения можно разделить на обыкновенные (ОДУ), в которые входят только функции (и их производные) от одного аргумента, и уравнения с частными производными (УРЧП), в которых входящие функции зависят от многих переменных. Существуют также стохастические дифференциальные уравнения (СДУ), включающие случайные процессы. В зависимости от комбинаций производных, функций, независимых переменных дифференциальные уравнения подразделяются на линейные и нелинейные, с постоянными или переменными коэффициентами, однородные или неоднородные. В связи с важностью приложений в отдельный класс выделены квазилинейные (линейные относительно старших производных) дифференциальные уравнения в частных производных. Для обыкновенных дифференциальных уравнений такие условия были сформулированы Рудольфом Липшицем (1864). Для уравнений в частных производных соответствующая теорема была доказана Софьей Ковалевской (1874). Решения дифференциальных уравнений подразделяются на общие и частные решения. Общие решения включают в себя неопределенные постоянные, а для уравнений в частных производных — произвольные функции от независимых переменных, которые могут быть уточнены из дополнительных условий интегрирования (начальных условий для обыкновенных дифференциальных уравнений, начальных и граничных условий для уравнений в частных производных). После определения вида указанных постоянных и неопределённых функций решения становятся частными. Обыкновенным дифференциальным уравнением n–ого порядка называется соотношение вида: 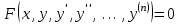 (1), (1),где 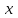 – независимая переменная; – независимая переменная; 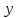 – искомая функция переменной; – искомая функция переменной; – производные искомой функции; – производные искомой функции; 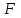 – известная функция своих аргументов. – известная функция своих аргументов.Считается, что производная 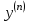 на самом деле входит в выражение (1), а величины на самом деле входит в выражение (1), а величины 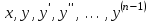 могут и не входить в него. могут и не входить в него.Порядком дифференциального уравнения, n, называется наивысший порядок производной, входящей в это уравнение. Пример. 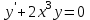 – уравнение первого порядка; – уравнение первого порядка;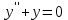 – уравнение второго порядка; – уравнение второго порядка;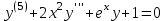 – уравнение пятого порядка. – уравнение пятого порядка.Всякая функция 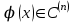 , которая, будучи подставленная вместо y в выражение (1), обращает это выражение в тождество, называется решением дифференциального уравнения (1). , которая, будучи подставленная вместо y в выражение (1), обращает это выражение в тождество, называется решением дифференциального уравнения (1).Если 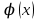 – решение, то по определению – решение, то по определению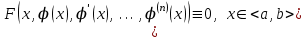 (2) (2)Пример. 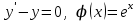 – решение, так как – решение, так как 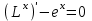 У рассматриваемого уравнения есть еще такое решение: 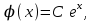 где С – произвольная постоянная. Это значит, что это уравнение имеет бесчисленное множество решений, зависящих от одного параметра (С). Можно показать, что уравнение n–ого порядка имеет семейство решений, зависящих от произвольных независимых друг от друга постоянных. Пример. Уравнение 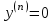 имеет решение: имеет решение: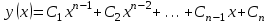 . .Процесс разыскания решения дифференциального уравнения называется интегрированием дифференциального уравнения. Решение дифференциального уравнения (1), содержащее n независимых между собой произвольных постоянных, называется его общим решением. 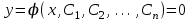 , (3) , (3)Дифференциальное уравнение может иметь не одно, а несколько общих решений. Например, для уравнения 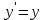 функции функции 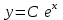 и и 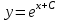 являются общими решениями, причем разными, так как первая из них обращается в нуль (С=0), а вторая – никогда в нуль не обращается. являются общими решениями, причем разными, так как первая из них обращается в нуль (С=0), а вторая – никогда в нуль не обращается.Соотношение 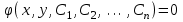 , (4) , (4)связывающее между собой независимую переменную, искомую функцию и n произвольных постоянных, называется общим интегралом уравнения (1). Следовательно, в общем интеграле решение задано в неявном виде. Пример. Рассмотрим уравнение: 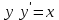 . Отсюда . Отсюда 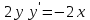 или или 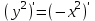 . Поэтому . Поэтому 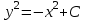 , где С – произвольная постоянная. , где С – произвольная постоянная.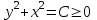 – общий интеграл; – общий интеграл; 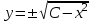 – общее решение. – общее решение.Решение, полученное из общего при фиксированных значениях произвольных постоянных, называется частным решением. Пример. Уравнение 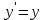 . Его общее решение . Его общее решение 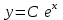 . Положим С=2, тогда . Положим С=2, тогда 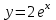 – частное решение. – частное решение.Особым решением по отношению к данному общему решению называется такое решение, которое не может быть получено ни при каких значениях произвольных постоянных, входящих в общее решение. Пример. Уравнение 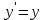 имеет два общих решения: имеет два общих решения:1) 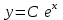 2) 2) 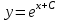 Решение: 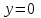 есть частное по отношению к первому и особое по отношению ко второму общему решению. есть частное по отношению к первому и особое по отношению ко второму общему решению.График частного решения называется интегральной кривой рассматриваемого дифференциального уравнения. Уравнение этой линии есть уравнение (3) и (4) при фиксированных 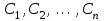 . .Таким образом, общее решение (или общий интеграл) определяет семейство интегральных кривых, каждая из которых соответствует определенному набору значений 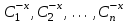 произвольных постоянных. произвольных постоянных.Для того чтобы дифференцировать выражение, где и определены и непрерывны в области плоскости и имеют в ней непрерывные частные производные и, представляла собой полный дифференциал некоторой функции, необходимо и достаточно, чтобы во всех точках области было выполнено условие. Интегрирующий множитель. Если уравнение не является уравнением в полных дифференциалах. Однако это уравнение можно превратить в уравнения в полных дифференциалах умножением на подходящую функцию. Такая функция называется интегрирующим множителем для данного дифференциального уравнения. Практически поступают так: берут выражение, делят на, если не зависит частное от, то находят по формуле, если в противном случае делят на и если частное не зависит от x, то существует и его находят по формуле. Для этого нужно найти функцию При соблюдении необходимых условий, гарантирующих существование общего интеграла существует и интегрирующий множитель (теорема о существовании интегрирующего множителя). Общий интеграл имеет бесчисленное множество интегрирующих множителей. Это свойство «неединственности» интегрирующего множителя и наличия зависимости между интегралами одного и того же уравнения имеют место и для всякого уравнения, у которого обеспечено существование общего интеграла (теорема о неединственности интегрирующего множителя). Примеры: 1. Дифференциальное уравнение 2. Аналогично для уравнения Как видим, уравнения в полных дифференциалах легко решаются, если знать функцию, дифференциалом которой является левая часть уравнения. Вспоминая определение потенциальности поля Теорема. Уравнение есть уравнение в полных дифференциалах тогда и только тогда, когда поле Если существуют непрерывные производны Это даёт возможность выяснить, является ли уравнение уравнением в полных дифференциалах или нет. Теорема позволяет найти решение уравнения. 3. Заключение В реферате было рассмотрено уравнения дифференциала (дифференциальные уравнения) в полных дифференциалах и интегрирующий множитель. Дифференциальные уравнения выступают математическими моделями различных явлений механики сплошной среды, химических реакций, электрических и магнитных явлений и др. Они представляет собой богатый содержанием, быстро развивающийся раздел математики. Уравнение в полных дифференциалах является одним из часто встречающихся дифференциальных уравнений. 4. Список использованных источников Конспект лекций по высшей математике: полный курс / Д. Т. Письменный. - 10-е изд., испр. - М.: Айрис-пресс, 2011г. - 608 с.: ил. - (Высшее образование); Фихтенгольц, Г.М. Основы математического анализа / Г.М. Фихтенгольц. - Часть 1. 6-е изд., стер. - СПб: Издательство «Лань», 2005. - 448с. https://studfile.net/preview/7901431/page:34/ http://www.phys.nsu.ru/balakina/difur_lecture.pdf https://www.bestreferat.ru/referat-412528.html http://www.tnu.in.ua/study/refs/d39/file468361.html |
