Математика. 5 вариант математика. Решение Вынесем 3xdx и 2ydy за скобки. Делаем замену ytx, тогда ytxt

• Название: Решение Вынесем 3xdx и 2ydy за скобки. Делаем замену ytx, тогда ytxt
• Анкор: Математика
• Дата: 17.05.2021
• Размер: 157.66 Kb.
• Имя файла: 5 вариант математика.docx
• Тип: Решение; #206175

Содержание

Задание 1 2

Задание 2 5

Задание 3 8

Задание 4 9

Задание 5 11

Список использованных источников 13

Задание 1

Условие:

Найти общий интеграл дифференциального уравнения.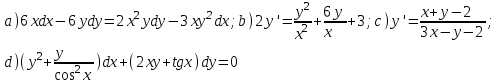


Решение: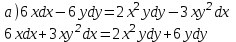



Вынесем 3xdx и 2ydy за скобки.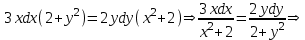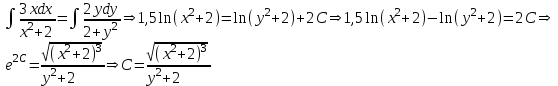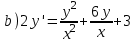







Делаем замену y=tx, тогда y’=t’x+t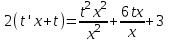



Сократив в правой части х² и х получим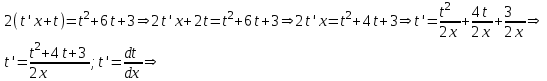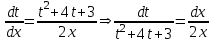





Проинтегрируем обе части уравнения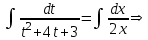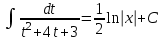





Найдем интеграл 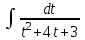разложим знаменатель по множителям.







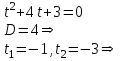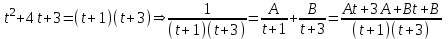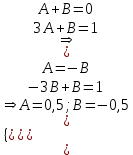Тогда: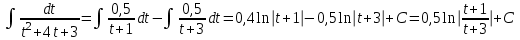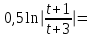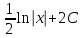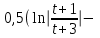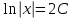







Делаем обратную замену: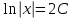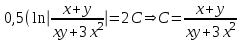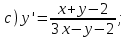







Сделаем замену: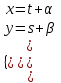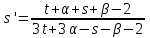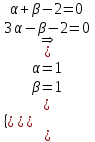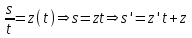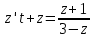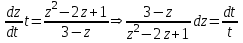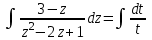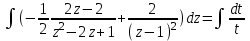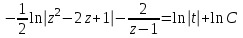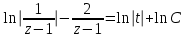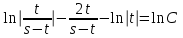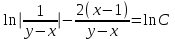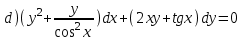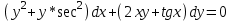





























P(x,y)dx+Q(x,y)dy=0. Здесь P(x,y)=y²+ysec²x, Q(x,y)=2xy+tgx. Заметим, что dP/dy=dQ/dx=2y+sec²x=dP/dy. Следовательно это уравнение в полных дифференциалах. du=0, u=const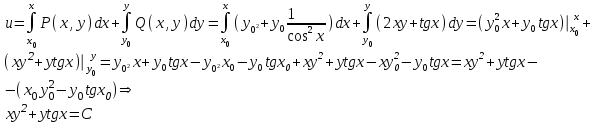

Задание 2

Условие:

Решить задачу Коши.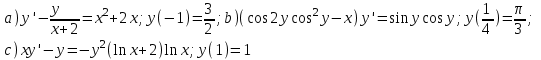


Решение: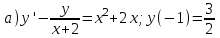



Найдем сначала решение дифференциального уравнения 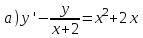Сделаем замену y=uv, y’=u’v-uv’



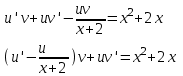Предположим: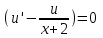

Тогда: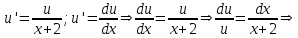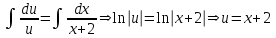



подставим в выражение uv’=x²+2x

(x+2)v’=x²+2x



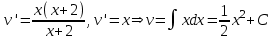Делаем обратную замену: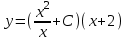



Подставим начальные условия: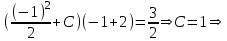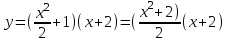



- решение задачи Коши



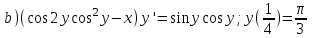Перепишем: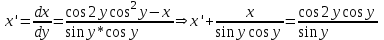

- это линейное уравнение.

Общее решение ищем в виде x=uv.

x’=u’v+uv’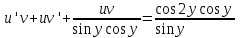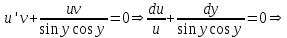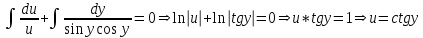







Тогда: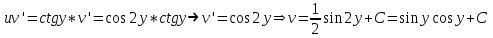



Тогда:

x= 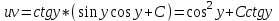- общее решение уравнения

Подставим начальные условия: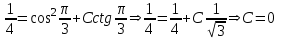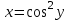



- решение задачи Коши.

















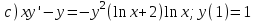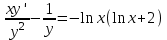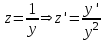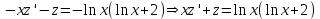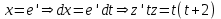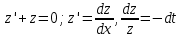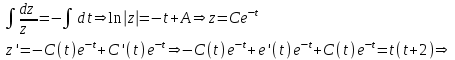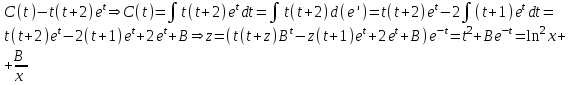В – производная константа

Z(1)=1, B=1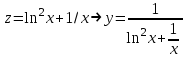

- решение задачи Коши.

Задание 3

Условие:

Решить дифференциальное уравнение

2yy’’-2(y’)²=y²
Решение: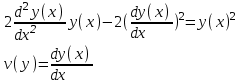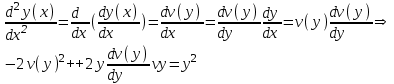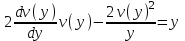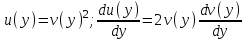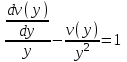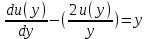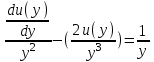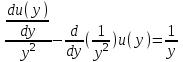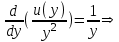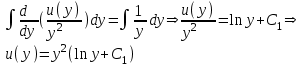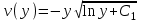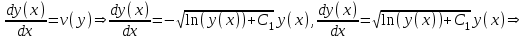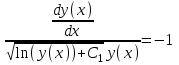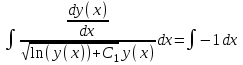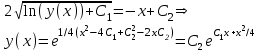

Задание 4

Условие:

Решить дифференциальные уравнения.

а) y’’-2y’-15y=0; b) y’’-16y’+15y=3e^x+x-2sinx
Решение:

а) y’’-2y’-15y=0

Данное дифференциальное уравнение относится к линейным дифференциальным уравнениям с постоянными коэффициентами.
Решение уравнения будем искать в виде y = e^rx. Для этого составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами:

r² -2 r +-15 = 0

D=2² – 4*(-15)=64

r₁=5; r₂=-3 - корни характеристического уравнения:

Следовательно, фундаментальную систему решений составляют функции:

у₁ = e^5x

у₂ = e^-3x

Общее решение однородного уравнения имеет вид: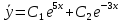



b) y’’-16y’+15y=3e^x+x-2sinx

Данное дифференциальное уравнение относится к линейным дифференциальным уравнениям с постоянными коэффициентами.
Решение уравнения будем искать в виде y = e^rx. Для этого составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами:

r² -16 r +15 = 0

D=16² – 4*1*15=196

r₁=15; r₂=1 - корни характеристического уравнения:

Следовательно, фундаментальную систему решений составляют функции:

y₂ = e^15x

y₁ = e^x

Общее решение однородного уравнения имеет вид: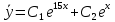

Задание 5

Условие:

Найти решение задачи Коши.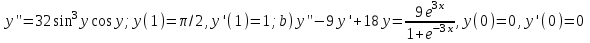


Решение: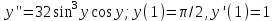



Сделаем замену p(y)=y’. Тогда y’’=p’p

Уравнение запишется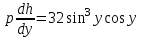

Интегрируем, разделив предварительно переменные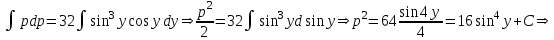



Подставим начальные условия: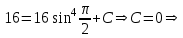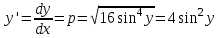





Разделим переменные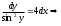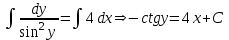





Подставляем условия: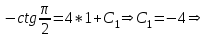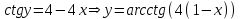



- решение задачи Коши





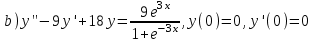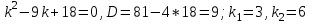Частные решения однородного уравнения y₁=e^3x, y₂=e^6x

Общее решение исходного уравнения ищем в виде:

Y=C₁(x)y₁(x)+C₂(x)y₂(x)

По методу вариации произвольных постоянных: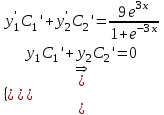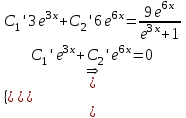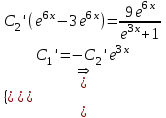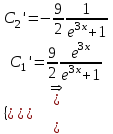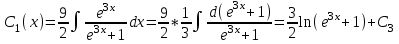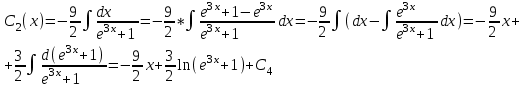









Общее решение исходного уравнения: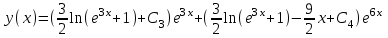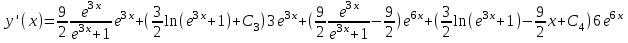





Подставим начальные условия: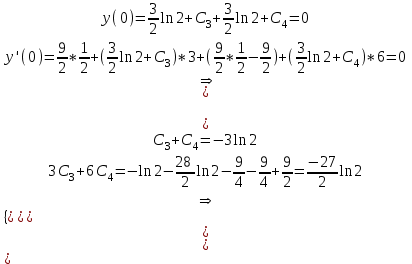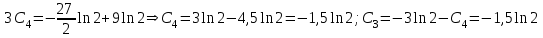





Тогда искомое решение: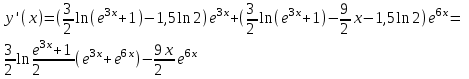

Список использованных источников

1. 
   Бугров, Я.С. Высшая математика в 3 т. Т.1 в 2 книгах. Дифференциальное и интегральное исчисление: Учебник для академического бакалавриата / Я.С. Бугров, С.М. Никольский. - Люберцы: Юрайт, 2016. - 501 c.
   
2. 
   Зельдович, Я.Б. Высшая математика для начинающих физиков и техников / Я.Б. Зельдович, И.М. Яглом. - М.: Ленанд, 2019. - 512 c
   
3. 
   Шипачев, В.С. Высшая математика. полный курс в 2 т. том 1: Учебник для академического бакалавриата / В.С. Шипачев. - Люберцы: Юрайт, 2016. - 288 c.