ИДЗ4. Решение уравнений Решение
 Скачать 33.73 Kb. Скачать 33.73 Kb.
|
|
Вариант 16 ИДЗ 4. Найти обще решение уравнений 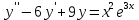 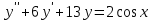 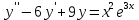 Решение. Рассматриваемое уравнение является линейным неоднородным дифференциальным уравнением второго порядка с постоянными коэффициентами. Его общее решение есть сумма общего решения соответствующего однородного уравнения и какого-нибудь частного решения исходного уравнения. Найдем сначала общее решение однородного уравнения:  Решим его характеристическое уравнение: 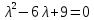 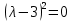  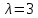 Так как 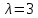 , то общее решение однородного уравнения , то общее решение однородного уравнениязапишется следующим образом:  Так как правая часть уравнения имеет вид 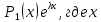 - многочлен первой степени, а число - многочлен первой степени, а число 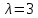 - корень кратности - корень кратности 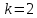 характеристического уравнения, то частное решение будет иметь вид: характеристического уравнения, то частное решение будет иметь вид: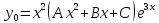 , где 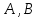 – неопределенные коэффициенты. Найдем – неопределенные коэффициенты. Найдем 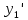 и и 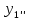 ,подставим предполагаемый вид частного решения в данное уравнение. ,подставим предполагаемый вид частного решения в данное уравнение.  Подставим полученные производные в исходное уравнение:   Вычислим коэффициенты: 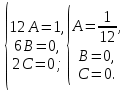 Подставляем полученные коэффициенты в  и получим: и получим: Таким образом,  Проверка. Найдем 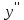 и и 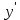 и подставим общее решение в данное уравнение. и подставим общее решение в данное уравнение.  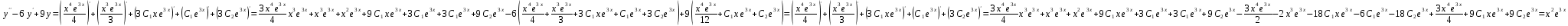 Таким образом, уравнение решено верно. Ответ: 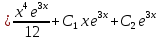 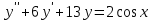 Решение. 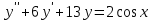 Рассматриваемое уравнение является линейным неоднородным дифференциальным уравнением второго порядка с постоянными коэффициентами. Его общее решение есть сумма общего решения соответствующего однородного уравнения и какого-нибудь частного решения исходного уравнения. Найдем сначала общее решение однородного уравнения: 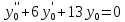 Из правой части уравнения  можно сделать вывод, что можно сделать вывод, что 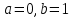 , то есть число , то есть число   Характеристические корни 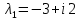 , , 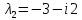 . При этом число . При этом число 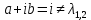 . .Соответственно, общим решением будет: 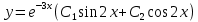 Частное решение будем искать методом неопределённых коэффициентов.  , ,, где 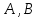 – неопределенные коэффициенты. Найдем – неопределенные коэффициенты. Найдем 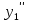 и и 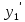 , подставим предполагаемый вид частного решения в данное уравнение: , подставим предполагаемый вид частного решения в данное уравнение: 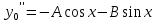 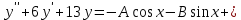   Найдем значения коэффициентов:  Подставляем полученные коэффициенты в  и получим: и получим: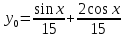 Таким образом,  Проверка. Найдем 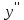 и и 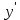 и подставим общее решение в данное уравнение. и подставим общее решение в данное уравнение.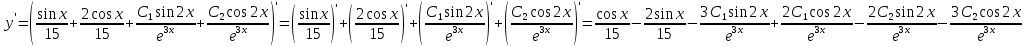 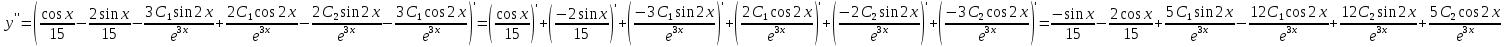  Ответ:  |
