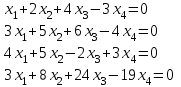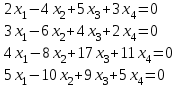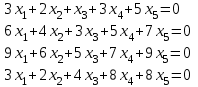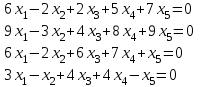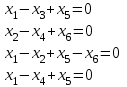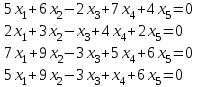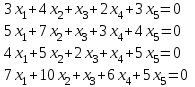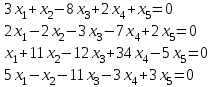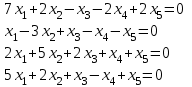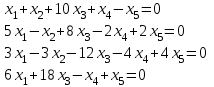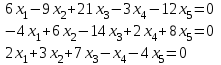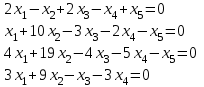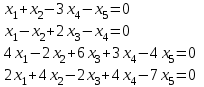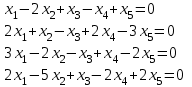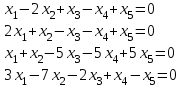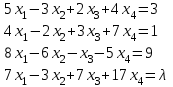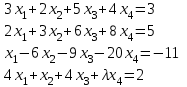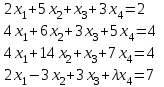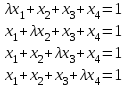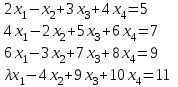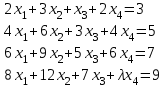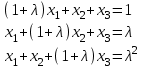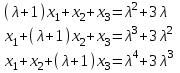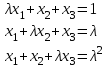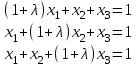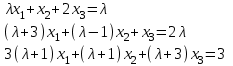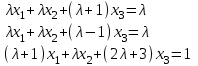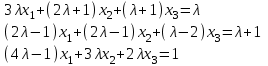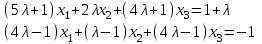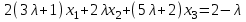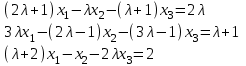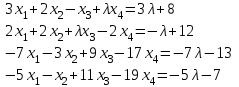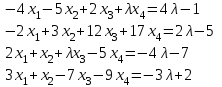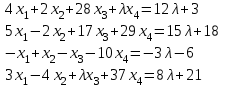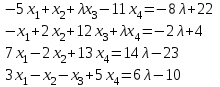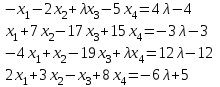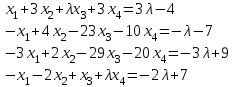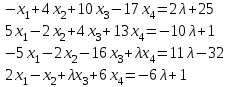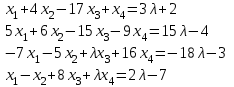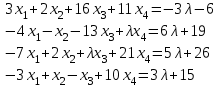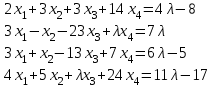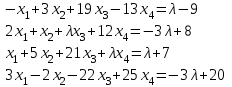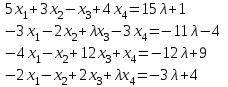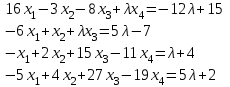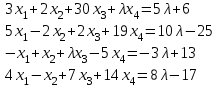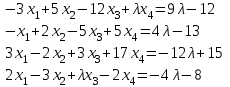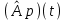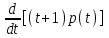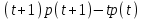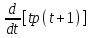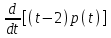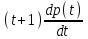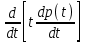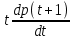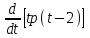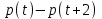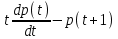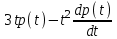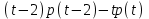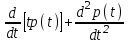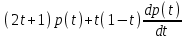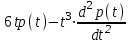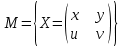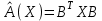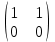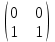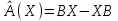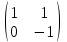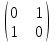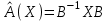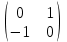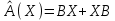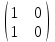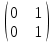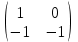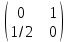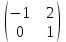Типовой расчет 2. Решение для однородной системы уравнений. вар. Система уравнений вар. Система уравнений 1, 20 2, 21
 Скачать 0.55 Mb. Скачать 0.55 Mb.
|
|
Типовой расчет №2 Практические заданияЗадача 1. Найти фундаментальную систему решений и общее решение для однородной системы уравнений.
Задача 2*. Найти общее решение в зависимости от значения параметра . При каких значениях система допускает решение с помощью обратной матрицы?
Задача 3. Линейный оператор 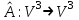 определяется действием отображения на концы радиус-векторов точек трехмерного пространства. определяется действием отображения на концы радиус-векторов точек трехмерного пространства.а) Найти матрицу оператора  в подходящем базисе пространства в подходящем базисе пространства 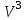 , а затем в каноническом базисе , а затем в каноническом базисе 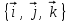 . б) В какую точку трехмерного пространства переходит точка с координатами (1, 0, 0) под действием отображения ? . б) В какую точку трехмерного пространства переходит точка с координатами (1, 0, 0) под действием отображения ?
Задача 4. а) Доказать, что оператор  является линейным оператором в пространстве является линейным оператором в пространстве 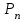 многочленов степени не выше n. многочленов степени не выше n. б) Найти его матрицу в каноническом базисе. в) Существует ли обратный оператор? Если да, найдите его матрицу. г) Опишите ядро оператора  , т. е. множество , т. е. множество 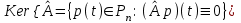 . .
Задача 5. Пусть А матрица оператора  из задачи 3 в каноническом базисе из задачи 3 в каноническом базисе  . Найдите собственные значения и собственные векторы матрицы А. Объясните, как полученный результат связан с геометрическим действием оператора . Найдите собственные значения и собственные векторы матрицы А. Объясните, как полученный результат связан с геометрическим действием оператора  . .Задача 6. Оператор  действует на матрицы, образующие линейное подпространство М в пространстве матриц второго порядка. действует на матрицы, образующие линейное подпространство М в пространстве матриц второго порядка. а) Доказать, что  линейный оператор в М. линейный оператор в М.б) Найти матрицу А оператора  в каком-нибудь базисе пространства М. в каком-нибудь базисе пространства М. в) Найти собственные значения и собственные векторы оператора  (напомним, что в этой задаче векторами являются матрицы). (напомним, что в этой задаче векторами являются матрицы).г) Доказать, что  оператор простого типа, описать его действие в собственном базисе. оператор простого типа, описать его действие в собственном базисе.
|