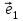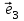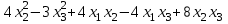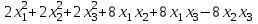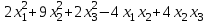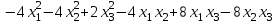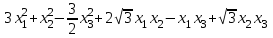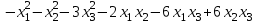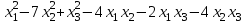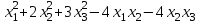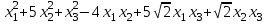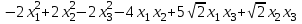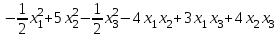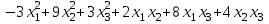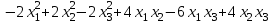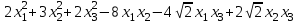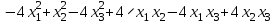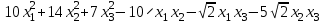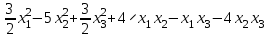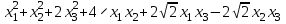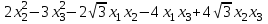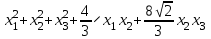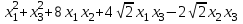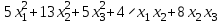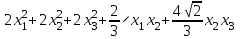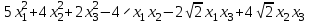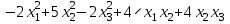Типовой расчет 2. Решение для однородной системы уравнений. вар. Система уравнений вар. Система уравнений 1, 20 2, 21
 Скачать 0.55 Mb. Скачать 0.55 Mb.
|
|
Задача 7. В пространстве 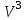 геометрических векторов с обычным скалярным произведением векторы базиса геометрических векторов с обычным скалярным произведением векторы базиса 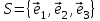 заданы координатами в базисе заданы координатами в базисе  . . а) Найдите матрицу Грама  скалярного произведения в этом базисе. Выпишите формулу для длины вектора через его координаты в базисе S. скалярного произведения в этом базисе. Выпишите формулу для длины вектора через его координаты в базисе S. б) Ортогонализуйте базис S. Сделайте проверку ортонормированности построенного базиса P двумя способами: выписав координаты векторов из P в каноническом базисе  ; ; убедившись, что преобразование матрицы Грама при переходе от базиса S к базису P (по формуле 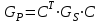 ) приводит к единичной матрице. ) приводит к единичной матрице.
Задача 8. Задана квадратичная форма. а) Привести ее к каноническому виду методом Лагранжа, записав соответствующее преобразование переменных. б) Привести ее к каноническому виду ортогональным преобразованием. в) Проверить закон инерции квадратичной формы на примерах преобразований, полученных в пунктах а), б).
Дополнительные теоретические упражнения 1. Доказать утверждения о связи решений однородной и неоднородной систем линейных уравнений: а) разность двух решений неоднородной системы является решением однородной системы; б) сумма решений неоднородной и однородной систем является решением неоднородной системы; в) общее решение неоднородной системы имеет вид Х = Х0 + Хч, где Хч частное решение неоднородной системы, Х0 общее решение однородной системы; г*) каков геометрический смысл последнего утверждения для системы уравнений с тремя неизвестными? 2. Доказать, что для любых различных чисел х1, х2, х3 и любых чисел y1, y2, y3 существует, причем единственный, многочлен y = f(x) степени не больше 2, для которого f(xi) = yi, i = 1, 2, 3. Когда степень этого многочлена меньше 2, равна 1, равна 0? 3. Пусть А прямоугольная матрица. Докажите, что r(A)=1 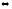 A = BC, где В вектор-столбец, С вектор-строка (r(А) ранг матрицы А; В, С ненулевые). A = BC, где В вектор-столбец, С вектор-строка (r(А) ранг матрицы А; В, С ненулевые).4. Пусть А прямоугольная матрица. Докажите, что всякое элементарное преобразование строк матрицы А можно представить в виде умножения матрицы А слева на некоторую матрицу Х, а всякое элементарное преобразование столбцов матрицы А в виде умножения матрицы А справа на некоторую матрицу Y. 5. Действие оператора  в n-мерном пространстве задается формулой преобразования координат векторов в некотором базисе: в n-мерном пространстве задается формулой преобразования координат векторов в некотором базисе: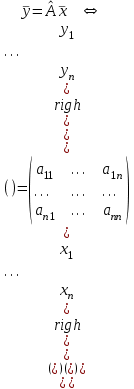 . .Доказать, что  линейный оператор и найти его матрицу в этом базисе. линейный оператор и найти его матрицу в этом базисе.6. Пусть  линейный оператор. Доказать, что если линейный оператор. Доказать, что если 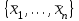 линейно зависимая система, то система линейно зависимая система, то система 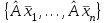 тоже линейно зависима. Верно ли обратное? тоже линейно зависима. Верно ли обратное?7. Доказать, что матрицы оператора в двух разных базисах совпадают тогда и только тогда, когда матрица оператора в одном базисе перестановочна с матрицей перехода от этого базиса ко второму. 8. Является ли оператор дифференцирования невырожденным в линейном пространстве L: а) L = Pn; б) L = L[cost, sint]? 9*. В пространстве всех многочленов заданы операторы  и и  : : 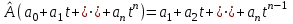 ; ;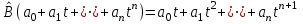 . .Доказать линейность операторов и проверить, что  . .10. Пусть  собственные векторы оператора собственные векторы оператора  , отвечающие различным собственным значениям. Доказать, что вектор , отвечающие различным собственным значениям. Доказать, что вектор  не является собственным вектором этого оператора. не является собственным вектором этого оператора. 11. Матрица А удовлетворяет условию 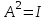 . Докажите, что всякая подобная ей матрица обладает тем же свойством. Что можно сказать о собственных числах матрицы А? Приведите пример такой недиагональной матрицы. . Докажите, что всякая подобная ей матрица обладает тем же свойством. Что можно сказать о собственных числах матрицы А? Приведите пример такой недиагональной матрицы.12. Ненулевая матрица А удовлетворяет условию 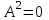 . Показать, что любая подобная ей матрица удовлетворяет этому условию. Диагонализуема ли матрица А? Каковы ее собственные значения? Привести пример такой матрицы. . Показать, что любая подобная ей матрица удовлетворяет этому условию. Диагонализуема ли матрица А? Каковы ее собственные значения? Привести пример такой матрицы.13. Функция 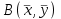 задается через координаты векторов в некотором базисе n-мерного пространства по формуле: задается через координаты векторов в некотором базисе n-мерного пространства по формуле: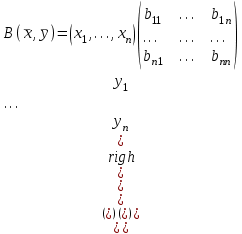 . .Доказать, что 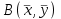 билинейная форма; найти ее матрицу в этом базисе. билинейная форма; найти ее матрицу в этом базисе. 14. Доказать, что симметричная билинейная форма 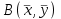 однозначно восстанавливается по порожденной ею квадратичной форме однозначно восстанавливается по порожденной ею квадратичной форме 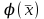 по формуле: по формуле: 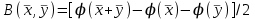 . . 15. Доказать, что если ненулевые векторы евклидова пространства 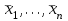 попарно ортогональны, то они линейно независимы. попарно ортогональны, то они линейно независимы. 16. Доказать, что в евклидовом пространстве справедливо неравенство треугольника: 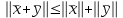 . Когда оно превращается в равенство? . Когда оно превращается в равенство?17*. Доказать, что если  линейный оператор в n-мерном пространстве, линейный оператор в n-мерном пространстве, имеющий n различных собственных значений, и  , то , то  обладает базисом из собственных векторов. обладает базисом из собственных векторов.18*. Пусть линейный оператор  удовлетворяет условию удовлетворяет условию 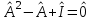 . Доказать, что . Доказать, что  обратим, и выразить обратим, и выразить 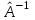 через через  . .19*. Пусть С невырожденная матрица. Доказать, что квадратичная форма, заданная в некотором базисе матрицей В = СТС (см. упр.10), положительно определена. 20*. Пусть  и и  линейные операторы в конечномерном пространстве L такие, что линейные операторы в конечномерном пространстве L такие, что  . Доказать, что . Доказать, что  обратим, и найти обратим, и найти 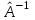 . (Указание: вопрос сводится к аналогичному вопросу для квадратных матриц.) Верно ли аналогичное утверждение в бесконечномерном пространстве? . (Указание: вопрос сводится к аналогичному вопросу для квадратных матриц.) Верно ли аналогичное утверждение в бесконечномерном пространстве?Вспомогательные контрольные вопросы Теория систем линейных уравнений. 1. Что такое ранг матрицы? Как он связан с рангом системы ее строк (столбцов)? Чему равен ранг матрицы, все элементы которой одинаковы? 2. Каков критерий равенства определителя нулю? 3. Что происходит с рангом матрицы: а) при ее транспонировании (и почему?); б) при элементарных преобразованиях? 4. Как выглядит блочно-треугольная матрица, чему равен ее ранг? 5. Что такое матрица системы; расширенная матрица? Что означают слова: записать систему в матричной форме? Почему она эквивалентна исходной системе уравнений? 6. Что означает совместность системы? Какие системы называются эквивалентными? Каков критерий совместности системы? Когда решение системы единственно? 7. Всегда ли совместна однородная система? Каков критерий существования ненулевых решений у однородной системы? Выделите случай квадратной системы. 8. Образует ли множество решений однородной системы линейное пространство? А множество решений неоднородной системы? Объясните результат. Какова связь решений однородной и неоднородной систем? 9. Какова размерность пространства решений однородной системы? Что называется фундаментальной системой решений (ФСР)? Почему понятие ФСР существует только для однородной системы? 10. Что называется общим решением однородной системы и какова его структура? Пусть дана ФСР некоторой однородной системы: 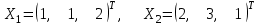 . .Выпишите все ее решения. Укажите другую ФСР этой системы. 11. Все решения однородной системы линейных уравнений могут быть записаны в виде: x1 = s + t, x2 = s 2t, x3 = 3, x4 = t, x5 = s + 2t, где s, tR. Укажите ее ФСР. Сколько уравнений могло быть в системе? 12. Все решения неоднородной системы линейных уравнений могут быть записаны в виде x = 1 + s, y = 2s 1, z = s. Опишите все решения соответствующей однородной системы и приведите пример ее ФСР. 13. Какие способы решения систем линейных уравнений Вы знаете? Всегда ли они применимы? |