Типовой расчет 2. Решение для однородной системы уравнений. вар. Система уравнений вар. Система уравнений 1, 20 2, 21
 Скачать 0.55 Mb. Скачать 0.55 Mb.
|
|
Линейные операторы. 1. Что такое линейный оператор? Привести примеры линейных операторов в пространствах 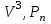 . Какой вектор сохраняется при действии любого линейного оператора? . Какой вектор сохраняется при действии любого линейного оператора?2. Какие из следующих отображений, действующих на геометрические векторы 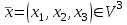 , являются линейными операторами (векторы , являются линейными операторами (векторы 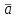 и и 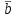 фиксированы): фиксированы): а)  ; б) ; б)  ; ; в) 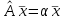 ; г) ; г) 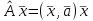 ; ; д) 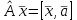 ; е) ; е) 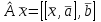 ; ; ж) 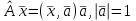 (каков геометрический смысл?); (каков геометрический смысл?);з) 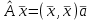 ; и) ; и) 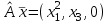 ; ;к) 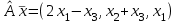 ; л) ; л)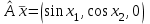 ; ;м)  поворот вокруг оси OZ на угол ; поворот вокруг оси OZ на угол ;н) 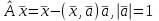 (каков геометрический смысл?). (каков геометрический смысл?).3. Какие из следующих отображений являются линейными операторами в пространстве L: а) 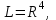 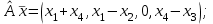 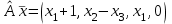 ; ;б) 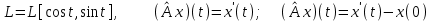 ; ;в) 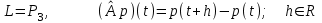 ; ;г) 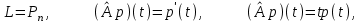 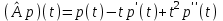 д) L=P – пространство всех многочленов (объяснить, почему это линейное пространство), 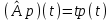 ; ; 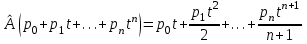 – интегрирование. – интегрирование.4. Что такое матрица линейного оператора в данном базисе? Как она изменится, если поменять местами два базисных вектора? Пусть линейный оператор  переводит векторы переводит векторы 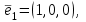 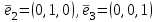 соответственно в векторы соответственно в векторы 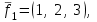 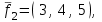  . Какова его матрица в базисе . Какова его матрица в базисе 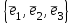 ? ?5. Известна матрица оператора в некотором базисе. По какой формуле преобразуются координаты векторов под действием этого оператора? 6. Что такое сумма, произведение линейных операторов? Что происходит с матрицами линейных операторов при сложении, умножении операторов? 7. Как образуется матрица перехода от данного базиса к новой системе векторов? Каков критерий базисности новой системы? Как преобразуются координаты векторов и матрица линейного оператора при переходе к другому базису? Что происходит при этом с определителем матрицы? 8. Какие матрицы называются подобными? Какие свойства подобия матриц Вы знаете? Как связаны между собой определители подобных матриц? Ответ на последний вопрос обоснуйте. 9. Какой оператор называется невырожденным? Что такое обратный оператор? Каков критерий его существования? Как найти матрицу обратного оператора? Известно, что линейный оператор  переводит вектор переводит вектор 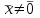 в нуль-вектор. Существует ли в нуль-вектор. Существует ли 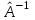 ? Ответ обосновать. ? Ответ обосновать.10. Что такое собственный вектор линейного оператора? Каков геометрический смысл собственного вектора в пространстве 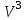 ? Пусть ? Пусть 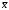 – собственный вектор. Укажите еще какой-нибудь собственный вектор, отвечающий тому же собственному значению. Ответ обосновать. Могут ли быть линейно зависимыми собственные векторы, отвечающие различным собственным значениям? – собственный вектор. Укажите еще какой-нибудь собственный вектор, отвечающий тому же собственному значению. Ответ обосновать. Могут ли быть линейно зависимыми собственные векторы, отвечающие различным собственным значениям?11. Верны ли утверждения: а) если 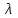 – собственное значение оператора – собственное значение оператора  , то , то 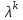 – собственное значение для оператора – собственное значение для оператора 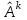 ; ; б) если 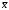 – собственный вектор операторов – собственный вектор операторов  и и  с собственными значениями с собственными значениями 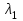 и и 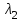 соответственно, то соответственно, то 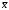 – собственный вектор для – собственный вектор для 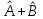 ; для ; для 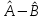 ? Если да, то с каким собственным значением? ? Если да, то с каким собственным значением? 12*. Исходя из геометрического смысла оператора 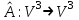 , указать его собственные значения и собственные векторы. Обладает ли он базисом из собственных векторов? Если да, то как выглядит матрица оператора в этом базисе? Является ли оператор невырожденным? а) , указать его собственные значения и собственные векторы. Обладает ли он базисом из собственных векторов? Если да, то как выглядит матрица оператора в этом базисе? Является ли оператор невырожденным? а)  – оператор проектирования векторов на плоскость P; б) – оператор проектирования векторов на плоскость P; б)  – оператор проектирования векторов на прямую L; в) – оператор проектирования векторов на прямую L; в)  – оператор симметрии векторов относительно плоскости P; г) – оператор симметрии векторов относительно плоскости P; г)  – оператор симметрии векторов относительно прямой L; – оператор симметрии векторов относительно прямой L;д) 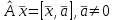 – фиксированный вектор. – фиксированный вектор.13. Что такое характеристический многочлен линейного оператора? Зачем он нужен? Как он зависит от выбора базиса? Пусть 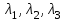 – собственные значения оператора в – собственные значения оператора в 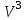 : а) каков его характеристический многочлен; б*) чему равен определитель матрицы оператора? : а) каков его характеристический многочлен; б*) чему равен определитель матрицы оператора? 14. Как находить собственные значения и собственные векторы линейного оператора в n-мерном пространстве? 15. Что такое оператор простого типа? Как выглядит матрица оператора в базисе из собственных векторов? Каково достаточное условие оператора простого типа? Является ли оно необходимым?* Что означает диагонализуемость матрицы? 16. Матрица оператора в некотором базисе – треугольная. Каковы собственные значения этого оператора? 17*. Интерпретируя матрицу А как матрицу линейного оператора, вычислить 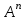 , где: а) А – треугольная матрица n-го порядка с нулевыми элементами на главной диагонали; , где: а) А – треугольная матрица n-го порядка с нулевыми элементами на главной диагонали; б) 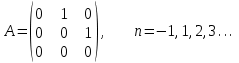 . .18*. Справедливо ли рассуждение: “Пусть 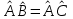 , где , где  – ненулевой оператор; сократив на – ненулевой оператор; сократив на  , получим , получим 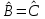 ”? ”?6.20*. Привести пример линейных операторов  и и  , для которых , для которых 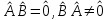 ( указание: см. 6.17*). ( указание: см. 6.17*). Билинейные и квадратичные формы. 1. Что такое билинейная форма? Как образуется матрица билинейной формы в данном базисе? Как записать билинейную форму в данном базисе? Как записать билинейную форму в координатной и в векторно-матричной записи? Пусть  – матрица формы в базисе – матрица формы в базисе 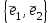 ; ; 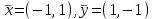 . Чему равны . Чему равны 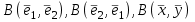 ? ? 2. При каком условии на коэффициенты билинейная форма 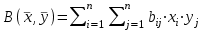 симметрична, кососимметрична? симметрична, кососимметрична?3. Как меняется матрица билинейной формы при изменении базиса? Что происходит при этом со значениями формы? 4. Что такое квадратичная форма? Как образуется матрица квадратичной формы в данном базисе? Как записать квадратичную форму по ее матрице (указать 2 вида записи)? Выпишите матрицу квадратичной формы 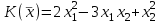 . Приведите векторно-матричную запись формы. Приведите два вида записи квадратичной формы с матрицей . Приведите векторно-матричную запись формы. Приведите два вида записи квадратичной формы с матрицей 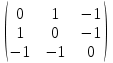 . .5. Каков канонический вид квадратичной формы? Однозначно ли он определен? Как выглядит матрица формы в каноническом базисе? Какие характеристики формы не зависят от выбора канонического базиса? 6. Что называется положительным, отрицательным индексами инерции, рангом квадратичной формы? Что означает положительная (отрицательная) определенность формы? Каковы положительный, отрицательный индексы и ранг положительно (отрицательно) определенной формы? 7. Каков критерий положительной (отрицательной) определенности квадратичной формы? 8. Поверхность 2-го порядка в 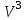 задается уравнением задается уравнением 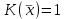 , где , где 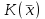 – квадратичная форма. Укажите тип поверхности в зависимости от ранга и индексов инерции квадратичной формы. – квадратичная форма. Укажите тип поверхности в зависимости от ранга и индексов инерции квадратичной формы.Евклидовы пространства. 1. Какие аксиомы определяют скалярное произведение в евклидовом пространстве? Что они означают на языке билинейных форм? Приведите примеры скалярных произведений. 2. Что такое матрица Грама? Каковы ее свойства? Как записать с ее помощью скалярное произведение векторов? Может ли матрица Грама в некотором базисе 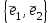 иметь вид: а) иметь вид: а)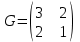 ; б) ; б) 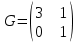 ; в) ; в) 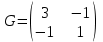 ? ? При положительном ответе найти 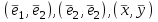 , где , где . . 3. Что такое длина (норма) вектора в евклидовом пространстве? Каковы ее свойства? Что такое неравенство Коши–Буняковского? Когда оно превращается в равенство? Как выглядит неравенство треугольника, и почему оно так называется? 4. Как вычисляется угол между векторами? Почему это определение угла корректно? Какие векторы называются ортогональными? Скалярное произведение в базисе 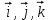 задается матрицей Грама задается матрицей Грама 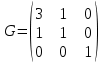 . Будут ли ортогональны векторы . Будут ли ортогональны векторы 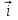 и и 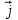 ; ; 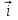 и и 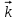 ; ; 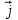 и и 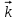 ? Каковы длины векторов ? Каковы длины векторов 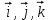 ? ?5. Что такое ортогональный, ортонормированный базисы в евклидовом пространстве? Как выглядит матрица Грама в ортогональном базисе, в ортонормированном? Как ищется скалярное произведение в ортонормированном базисе? Почему? Как выражаются через скалярное произведение координаты вектора в ортонормированном базисе? Линейные операторы в евклидовом пространстве. 1. Какой оператор А* называется сопряженным к линейному оператору А в евклидовом пространстве? Будет ли он единственным? Как найти его матрицу, зная матрицу оператора А в ортонормированном базисе? 2. Как найти оператор, сопряженный к произведению операторов АВ; к их сумме А+В? Чему равен сопряженный оператор к обратному оператору 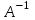 ? ?3. Какой оператор называется самосопряженным? Каково характеристическое свойство матрицы самосопряженного оператора в ортонормированном базисе? Сохраняется ли самосопряженность при сложении операторов; при умножении их на числа; при умножении операторов? 4. Какова специфика корней характеристического уравнения для самосопряженного оператора? Каковы свойства его собственных векторов? 5. Какой оператор называется ортогональным? Что происходит с ортонормированным базисом при действии ортогонального оператора? 6. Известно, что линейный оператор переводит ортонормированный базис в ортонормированный. Каков этот оператор? 7. Будет ли ортогональный оператор иметь обратный? Если да, то как его найти? 8. Известно, что оператор А обратим, и 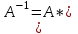 . Каков этот оператор? . Каков этот оператор?9. Каковы свойства матрицы ортогонального оператора в ортонормированном базисе? 10*. Как показать, что при переходе от одного ортонормированного базиса к другому ортонормированному базису матрица самосопряженного оператора преобразуется так же, как матрица соответствующей квадратичной формы? Для чего здесь нужна самосопряженность оператора? Вспомогательная учебная литература 1. Головина Л. И. Линейная алгебра и некоторые ее приложения. – М.: Наука, 1985. 2. Линейная алгебра и основы математического анализа. Сборник задач по математике для втузов. Ред. Ефимов А. В., Демидович Б. П. – М.: Наука, 1986. 3. Рублев А. Н. Курс линейной алгебры и аналитической геометрии. – М.: Высшая школа, 1972. |
