плоскость и прямая. курсовая С.Н. геометрия. Плоскость и прямая
 Скачать 219.05 Kb. Скачать 219.05 Kb.
|
|
Пензенский Государственный Университет Кафедра «Математика и суперкомпьютерное моделирование» Тема курсовой работы «Плоскость и прямая» Выполнила: студентка гр. 21ВМ1 Сайдиева Н.П. Проверила: к.физ.-мат. н., доцент кафедры «МСМ» Деревянчук Е.Д. Содержание : Введение Плоскость в пространстве Общее уравнение плоскости Угол между прямой и плоскостью Точка пересечения прямой с плоскостью Прямая в пространстве Общее уравнение прямой Угол между прямой и плоскостью Координаты точки пересечения прямой и плоскости Задачи Заключение Список литературы 1.Введение Прямая и плоскость в пространстве. Всякое уравнение первой степени относительно координат Ax+By+Cz=0 (1) задает плоскость, и наоборот: всякая плоскость может быть представлена уравнением (1), которое называется уравнением плоскости. Вектор Особые случаи уравнения (1): D = 0, Ах + By + Cz = 0 - плоскость проходит через начало координат. С = 0, Ах + By + D = 0 - плоскость параллельна оси Oz. С = D = 0, Ах + By = 0 - плоскость проходит через ось Oz. С = В = 0, Ах + D = 0 - плоскость параллельна плоскости Oyz. Уравнения координатных плоскостей: Прямая в пространстве может быть задана: как линия пересечения двух плоскостей, т.е. системой уравнений: двумя своими точками 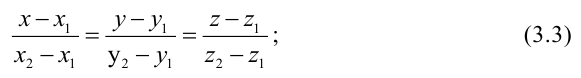 точкой 2.Плоскость в пространстве 2.1. Общее уравнение прямой Определение: Уравнение вида Определение: Порядок поверхности определяется по высшему показателю степени переменных х, у и z или по сумме показателей степени в произведении этих величин. Определение: Уравнение вида Ax+By+Cz+D=O называется общим уравнением плоскости. Рассмотрим частные случаи приведенного уравнения: 1. D = 0; Ах + By + Сz = 0. Из этого уравнения видно, что точка О(0; 0; 0) удов- летворяет этому уравнению, следовательно, это уравнение описывает плоскость, проходящую через начало координат (Рис. 1). 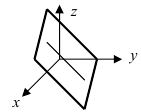 Рис. 1. Плоскость, проходящая через начало координат. Рис. 1. Плоскость, проходящая через начало координат.2. С = 0; Ах + Ву + D = 0. Этому уравнению удовлетворяет любое значение переменной z, поэтому данное уравнение описывает плоскость, которая параллельна оси аппликат (Oz) (Рис. 2). 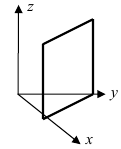 Рис. 2. Плоскость, проходящая параллельно оси аппликат. Рис. 2. Плоскость, проходящая параллельно оси аппликат.Замечание: При отсутствии в уравнении плоскости одной из переменных величин говорит о том, что плоскость параллельна соответствующей координатной оси. 3. С=0; D=0; Ах+ By=0 - плоскость проходит через начало отсчета параллельно оси аппликат (Рис. 3). 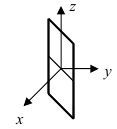 Рис. 3. Плоскость, проходящая через начало координат параллельно оси аппликат. Рис. 3. Плоскость, проходящая через начало координат параллельно оси аппликат.4. 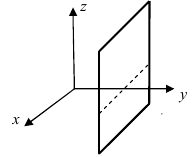 Рис. 4. Плоскость, проходящая параллельно координатной плоскости Рис. 4. Плоскость, проходящая параллельно координатной плоскости А = С = 0; Ву + D = 0 - плоскость проходит через точку плоскости 5. В = С = D = 0; Ах = 0=>х = 0 - уравнение описывает плоскость 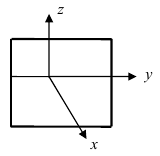 Рис. 5. Координатная плоскость 2.2. Угол между прямой и плоскостью 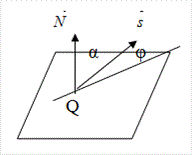 Угол α между нормальным вектором плоскости 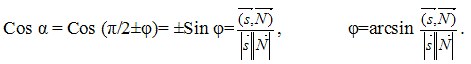 Пучок плоскостей Определение: Совокупность всех плоскостей, проходящих через заданную прямую L, называется пучком плоскостей, а прямая L - осью пучка. Пусть ось пучка задана уравнениями: 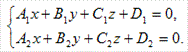 Умножим второе уравнение системы на постоянную и сложим с первым уравнением: A1x+B1y+C1z+D1+ λ(A2x+B2y+C2z+D2)=0. Это уравнение имеет первую степень относительно х, у, z и, следовательно, при любом численном значении λ определяет плоскость. Так как данное уравнение есть следствие двух уравнений, то координаты точки, удовлетворяющие этим уравнениям будут удовлетворять и данному уравнению. Следовательно, при любом численном значении λ данное уравнение есть уравнение плоскости, проходящей через заданную прямую. Полученное уравнение есть уравнение пучка плоскостей. 2.3. Точка пересечения прямой с плоскостью Пусть плоскость Q задана уравнением общего типа: Ax+By+Cz+D=0, а прямая L в параметрическом виде: x=x1+mt, y=y1+nt, z=z1+pt, тогда чтобы найти точку пересечения прямой L и плоскости Q, нужно найти значение параметра t, при котором точка прямой будет лежать на плоскости. Подставив значение x, y, z, в уравнение плоскости и выразив t, получим Значение t будет единственным, если прямая и плоскость не параллельны. Условия параллельности и перпендикулярности прямой и плоскости: Рассмотрим прямую L: и плоскость α: Ax+By+Cz+D=0. Прямая L и плоскость α: а) перпендикулярны друг другу тогда и только тогда, когда направляющий вектор прямой 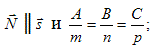 б) параллельны друг другу тогда и только тогда, когда векторы 3.Прямая в пространстве Прямая линия в пространстве бесконечна, поэтому задавать ее удобнее отрезком. Из школьного курса Евклидовой геометрии известна аксиома, «через две точки в пространстве можно провести прямую и, притом, только одну». Следовательно, на эпюре прямая может быть задана двумя фронтальными и двумя горизонтальными проекциями точек. Но так как прямая - это прямая (а не кривая), то с полным основанием мы можем соединить эти точки отрезком прямой и получить фронтальную и горизонтальную проекции прямой (рис. 13). 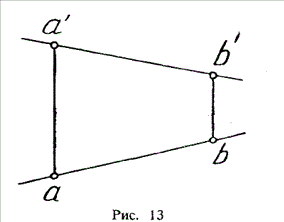 Доказательство от обратного: в плоскостях проекций V и Н заданы две проекции а' b' и ab (рис.14). Проведем через них плоскости, перпендикулярные к плоскостям проекций V и Н (рис.14), линией пересечения плоскостей будет прямая АВ. 3.1.Общее уравнение прямой Прямая в пространстве может быть задана как пересечение двух плоскостей: 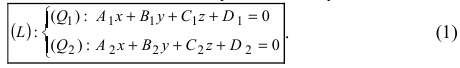 Определение: Геометрическое место точек пространства, удовлетворяющих системе уравнений (1), называется прямой в пространстве, а система уравнений (1) называется общим уравнением прямой. Замечание: Для того чтобы система уравнений (1) определяла прямую в пространстве необходимо и достаточно, чтобы нормальные вектора плоскостей, определяющих прямую, Пусть прямая проходит через точку  Замечание: Если в уравнении (2) одна из проекций направляющего вектора равна 0, то это означает, что прямая перпендикулярна соответствующей координатной оси. 3.3.Координаты точки пересечения прямой и плоскости Пусть прямая (L) задана общим уравнением  а плоскость (Q) уравнением Ax+By+Cz+D=0. Так как точка пересечения прямой и плоскости принадлежит одновременно обоим этим объектам, то ее координаты находят из системы уравнений:  Если прямая (L) задана каноническим уравнением Если прямая (L) задана каноническим уравнением  а плоскость (Q) уравнением Ax + By + Cz + D = 0, тo поступают по следующей схеме: переходят от канонического уравнения прямой к параметрическому, т.е. записывают уравнение прямой в виде  полученные выражения подставляют в уравнение заданной плоскости и находят параметр t: вычисляют координаты точки пересечения, подставив найденное значение  Рассмотрим возможные случаи: если выполняются условия при условиях если 3.2.Угол между прямой и плоскостью Метод прямоугольного треугольника Прямая общего положения, наклонена к плоскостям проекций под некоторым произвольным углом.  Угол между прямой и плоскостью определяется углом, составленным прямой и ее проекцией на эту плоскость (рис. 22). Угол a определяет угол наклона отрезка АВ к плоскости Н. В прямоугольном треугольнике AВb1 катет Ab1 равен горизонтальной проекции ab; а другой катет Вb1 равен разности расстояний точек А и В от плоскости Н. Если из точки В на горизонтальной проекции прямой ab проведем перпендикуляр и отложим на нем величину Z,то, соединив точку а с полученной точкой b0, получим гипотенузу аb0, равную натуральной величине отрезка АВ. На эпюре это выглядит так (рис. 23): Аналогично определяется угол наклона прямой к фронтальной плоскости проекций (b) - рис. 24. Замечание: при построениях на горизонтальной проекции прямой мы откладываем на вспомогательной прямой величину Z; при построениях на фронтальной проекции - величину Y.   Рассмотренный метод носит название прямоугольного треугольника. С его помощью можно определить натуральную величину любого интересующего нас отрезка, а также углы его наклона к плоскостям проекций. Взаимное положение прямых Если точка принадлежит прямой, то ее проекции лежат на одноименных проекциях прямой (правило принадлежности, см. рис. 14). Из школьного курса геометрии знаем , что две прямые пересекаются в одной точке (или: если две прямые имеют одну общую точку, то они пересекаются в этой точке). Проекции пересекающихся прямых на эпюре имеют ярко выраженный признак: проекции точки пересечения лежат на одной линии связи (рис. 25). Действительно: точка К принадлежит и АВ, и CD; на эпюре точка k' лежит на одной линии связи с точкой k. Проекции прямого угла Если две прямые общего положения пересекаются пол прямым углом, то их проекции образуют угол, не равный 90° (рис. 31). А так как при пересечении двух параллельных плоскостей третьей в пересечении получаются параллельные прямые, то горизонтальные проекции ab и cd - параллельны. Если повторить операцию и спроецировать прямые АВ и CD на фронтальную плоскость проекций, мы получим тот же результат.   4.Задачи №1(42 по Богомолову Н.В.). Составить уравнение плоскости, проходящей через точку М(-1; 2; -3) перпендикулярно прямой (x+2)/4=(z+3)/2. Решение : Очевидно , что в данной задаче нормального вектора искомой плоскости можно взять параллельный ему направленный вектор q равный (4; 3; 2) данной прямой. Остается воспользоваться уравнением плоскости, проходящей через данную точку М перпендикулярно вектору q. 4(x+1)+3(y-2)+2(z+3)=0, или 4x+3y+2z+4=0. №2 (45 по Богомолову). Убедиться в том, что прямая (x-2)/4=(y+4)/3=(z-1)/(-2) параллельна плоскости 5x-2y+7z+3=0. Решение: Используя условие параллельности прямой и плоскости, получаем 5*4+(-2)*3+7(-2)=0, т.е. прямая и плоскость параллельны . №3( 52 по Богомолову ) Найдите точку пересечения прямой (x+3)/2=(y-1)/3=(z+5)/2 с плоскостью 2x+3y+z-22=0. Решение: L: (x+3)/2=(y-1)/3=(z+5)/2 , следовательно  2x+3y+z-22=0 , следовательно 2*(  ) +3*( ) +3*(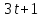 )+( )+(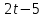 )-22=0, отсюда )-22=0, отсюда 4t -6+9t+3+2t-5-22=0 , 15t=30, t=30/15 , t=2. 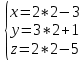 , следовательно точка М(1; 7 4 -1). , следовательно точка М(1; 7 4 -1).№4( 53 по Богомолову ). Составьте уравнение перпендикуляра к плоскости x-3y+2z-26=0, проходящей через точку (-2; 2; -4). Найдите координаты основания этого перпендикуляра. Решение: Из условия нам понятно , что плоскость(l) перпендикулярна прямой(n) , следовательно, 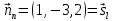 , отсюда , отсюда Уравнение будет такое : (x+2)/1=(y-2)/(-3)=(z-4)/2. №5( 54 по Богомолову ) Проверьте, что прямая (x-1)/(-2)=(y-4)/(-3)=(z+1)/3 параллельна плоскости 3x-5y-3z-4=0. Решение: Направляющий вектор прямой имеет координаты (-2;-3;3) Нормальный вектор плоскости имеет координаты (3;-5;–3) Если прямая параллельна плоскости, то ее направляющий вектор и нормальный вектор плоскости взаимно перпендикулярны. Векторы перпендикулярны, значит скалярное произведение векторов равно нулю. (-2)*3+(-3)*(-5)+3*(-3)=0 Значит прямая параллельна плоскости. №6( 55 по Богомолову ) Проверьте , что прямая (x-1)/2=(y+3)/(-1)=(z-4)/5 лежит в плоскости 3z-4y-2z-7=0. Решение: Проверить лежит ли прямая (x-1) / 2=(y+3)/ (-1)=(z+2) / 5 на плоскости 4x+3y+z+3=0 . n (3;-4;-2) → нормальный вектор плоскости ; s(2; -1; -5) →направляющий вектор прямой ; M₀(1;-3;4) _произвольная точка на прямой. составим скалярное произведение : n.s =3*2+(-4)*(-1)+(-2)*(-5) =0 ⇒ n ⊥ s , т.е. прямая параллельно плоскости или лежит на ней, но точка M₀(1;-3;4) не лежит на плоскости, действительно n * M₀≠0 (не удовл. уравн.),значит прямая не лежит на плоскости. №7( 56 по Богомолову). Составьте уравнение плоскости, проходящей через прямую 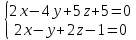 и точку M(3; 2; 1). и точку M(3; 2; 1).Решение: Запишем уравнение пучка плоскостей, проходящей через данную прямую: 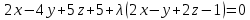 Так как координаты точки М должны удовлетворять уравнению плоскости, то , подставим их в соотношении x=3, y=2, z=1, имеем 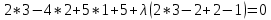 или 8+5 или 8+5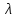 =0. =0.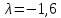 Подставим найденное лямбда в соотношение и получим ответ . Подставим найденное лямбда в соотношение и получим ответ .5.Заключение В данной работе описаны и рассмотрены «Прямая и плоскость в пространстве». Даны их основные понятия , так же были рассмотрены точки пересечения прямой и плоскости , угол между ними. В дополнение о плоскости , рассказывается про общие уравнение плоскости , также и про общее уравнение прямой . Немало важная тема – это пучок плоскостей , про которую написано выше . В курсовой работе были решены задачи , такие как : Нахождение уравнения плоскости. Нахождения точки пересечения. Нахождение принадлежности прямой к плоскости . Нахождение параллельности плоскости и прямой. 6.Список литературы Богомолов Н.В. Учебное пособие для ссузов (2003 , Высшая школа ) Стереометрия. Геометрия в пространстве. Александров А.Д., Вернер А.Л., Рыжик В.И. Ильин В. А., Позняк Э. Г. Аналитическая геометрия: Учеб. для вузов. - 7-е изд., стер., 2004. - 224 с. - (Курс высшей математики и математической физики.) Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры, 2005. - 304 с. |
