Уравнение плоскости, проходящей через три точки находится по формуле
 Скачать 5.25 Mb.
|
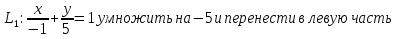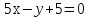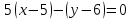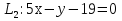          Уравнение плоскости, проходящей через три точки находится по формуле: 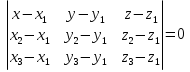 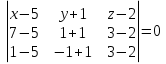   Прямая, заданная как пересечение двух плоскостей перпендикулярна нормалям обеих плоскостей, поэтому направляющий вектор прямой 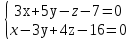 можно найти как векторное произведение нормалей заданных плоскостей.Для плоскости P1: 3x+5y-z−7=0 нормальный вектор имеет координаты N1(3,5,-1); для плоскости P2: x-3y+4z−16=0, нормальный вектор имеет координаты N2(1,-3,4). 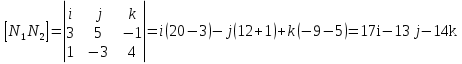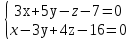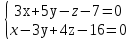Находим векторное произведение:  Таким образом, направляющий вектор прямой ; имеет координаты S¯(17,-13,-14).Пусть z=1, тогда 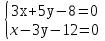 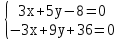 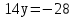 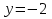  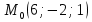 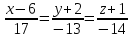 Уравнение прямой пересечения плоскостей 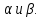  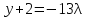 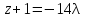 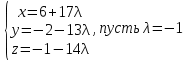 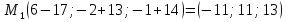 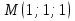 Теперь необходимо найти уравнение плоскости, проходящей через точки M, M0, M1.  Ответ: 18x+30y-7z-41=0  Найти значения переменных x1...x2, при которых функция:
принимает минимальное значение, при условии следующих ограничений :
x1, x2 ≥ 0 Шаг:1 Избавимся от неравенств в ограничениях, введя в ограничения 1, 2, 3 неотрицательные балансовые переменные s1, s2, s3.
x1, x2, s1, s2, s3 ≥ 0 Шаг:2 Ищем в системе ограничений базисные переменные. Из последней системы ограничений можно выделить базисные переменные s2,s3. Не все уравнения содержат базисные переменные, это значит, что исходная задача не содержит в себе допустимого базисного решения. Для его нахождения вначале составим и решим вспомогательную задачу. Такое решение еще называют решением с искусственным базисом. Введем в уравнение 1 искусственную неотрицательную переменную r1 . Получим следующую систему ограничений,
x1, x2, s1, s2, s3, r1 ≥ 0 с базисными переменными r1,s2,s3.
Целью решения вспомогательной задачи является получение допустимого базисного решения не содержащего искусственных переменных (r1). Для этого сформируем вспомогательную целевую функцию :
и проведем ее минимизацию в заданной системе ограничений. Если после минимизации функции G ее оптимальное значение будет равно нулю и все искусственные переменные окажутся выведенными из базиса, то полученное базисное решение есть допустимое базисное решение исходной задачи. Если же после минимизации функции G ее оптимальное значение окажется отличным от нуля, значит исходная система ограничений противоречива (область допустимых решений пуста) и исходная задача решения не имеет. Для решения вспомогательной задачи симплекс-методом выразим функцию G через свободные переменные, для этого: - вычтем из функции G уравнение 1 Функция G примет вид :
Теперь мы можем сформировать начальную симплекс-таблицу. Шаг:3 Начальная симплекс-таблица
Итерация 0-a
Получено оптимальное решение вспомогательной задачи (найден минимум функции G т.к. в строке целевой функции нет отрицательных коэффициентов). Все искусственные переменные вышли из базиса и поэтому мы можем приступить к решению исходной задачи, приняв полученное базисное решение в качестве опорного. Сторка "G" нам больше не нужна, принятие решения о направляющем столбце, во всех последующих итерациях, будем принимать по строке "Q" Итерация 1
Достигнуто оптимальное решение, т.к. в строке целевой функции нет отрицательных коэффициентов. Ответ:
достигается в точке с координатами:
Решение задачи ЛП онлайн симплекс-методом Целевая функция: -3X1-2X2+1X3→min Условия: -3X1+1X2+2X3≤3 1X1+2X2+3X3≤14 2X1+1X2+3X3≤16 Приведем систему ограничений к каноническому виду, для этого необходимо неравенства преобразовать в равенства, с добавлением дополнительных переменных. Если в преобразуемом неравенстве стоит знак ≥, то при переходе к равенству знаки всех его коэффициентов и свободных членов меняются на противоположные. Тогда система запишется в виде: -3X1+1X2+2X3+X4=3 1X1+2X2+3X3+X5=14 2X1+1X2+3X3+X6=16 Переходим к формированию исходной симплекс таблицы. В строку F таблицы заносятся коэффициенты целевой функции. Из данных задачи составляем исходную симплекс таблицу.
Так как в столбце свободных членов нет отрицательных элементов, то найдено допустимое решение.В строке F имеются отрицательные элементы, это означает что полученое решение не оптимально. Определим ведущий столбец. Для этого найдем в строке F максимальный по модулю отрицательный элемент - это -3 Ведущей строкой будет та для которой отношение свободного члена к соответствующему элементу ведущего столбца минимально. Ведущей строкой является X6, а ведущий элемент: 2.
В строке F имеются отрицательные элементы, это означает что полученое решение не оптимально. Определим ведущий столбец. Для этого найдем в строке F максимальный по модулю отрицательный элемент - это -0.5 Ведущей строкой будет та для которой отношение свободного члена к соответствующему элементу ведущего столбца минимально. Ведущей строкой является X5, а ведущий элемент: 1.5.
Так как в строке F нет отрицательных элементов, то найдено оптимальное решение. Так как исходной задачей был поиск минимума, оптимальное решение есть свободный член строки F, взятый с противоположным знаком. Найдено оптимальное решение F=-26 при значениях переменных равных: X2=4, X1=6, | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||