Лабораторная работа № 1
ИЗУЧЕНИЕ ЗАТУХАЮЩИХ МЕХАНИЧЕСКИХ КОЛЕБАНИЙ ПРУЖИННОГО МАЯТНИКА
Цель работы - определение декремента затухания, силы сопротивления вязкой среды, и добротности колебательной системы при колебаниях подвешенного на пружине тела в вязкой среде.
Теоретические основы работы
Пружинным маятником называется система, состоящая из упругой пружины и груза подвешенного на ней. В общем случае движение пружинного маятника в поле силы тяжести довольно сложно и описывается большим числом степеней свободы. Практический интерес, однако, представляют колебания с одной степенью свободы, когда движение маятника происходит вдоль вертикальной оси.

Рис. 10.1
Для полного описания колебаний в этом случае необходимо знать поведение только одной переменной, например, вертикальной координаты центра масс тела маятника. Теоретически пружинный маятник может совершать незатухающие механические колебания при условии, что пружина является идеально упругой, а тело движется в окружающей среде без трения. На тело, подвешенное на пружине в поле силы тяжести, действуют две силы (без учета сил трения) сила тяжести  и упругая сила и упругая сила  . Начало координат выберем в центре тяжести тела. При этом сила тяжести будет скомпенсирована некоторым начальным растяжением пружины, Δl в дальнейшем рассмотрении участвовать не будет. . Начало координат выберем в центре тяжести тела. При этом сила тяжести будет скомпенсирована некоторым начальным растяжением пружины, Δl в дальнейшем рассмотрении участвовать не будет.
При отклонении тела от точки равновесия будет возникать возвращающая сила F(х). Рассмотрим колебания пружинного маятника с малой амплитудой. Для пружинного маятника условия малости колебаний удовлетворяются при смещениях, Уравнение движения пружинного маятника при этом имеет вид
 (10.1) (10.1)
где: k - коэффициент жесткости пружины, m - масса маятника.
Если физическая величина x(t) изменяется со временем по гармоническому закону
 , (10.2) , (10.2)
то колебания называются гармоническими. В функции (10.2) А — амплитуда колебаний; w - круговая частота
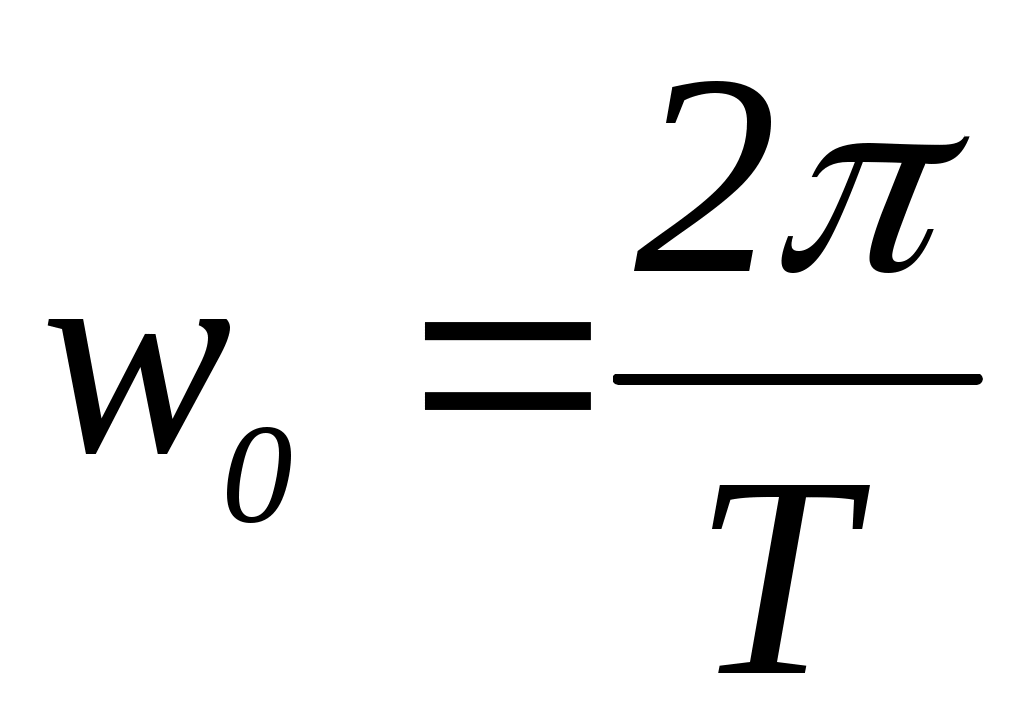 ; ;
T — период колебаний; t — время, пошедшее от начала колебаний; φ0—начальная фаза колебаний. Функция х(t) из (10.1) представляет решение дифференциального уравнения
 , (10.3) , (10.3)
называемого уравнением свободных колебаний. Физическую систему, выведенную из состояния равновесия и представленную самой себе, в которой изменение одного из параметров х описывается дифференциальным уравнением (10.3) называют классическим гармоническим осциллятором. Сравнивая (10.2) с (10.3), получим
 . (10.4) . (10.4)
В реальных осцилляторах, за счет сил сопротивления (в большей степени трения), происходит рассеяние (диссипация) запасенной энергии, в результате чего свободные колебания со временем затухают. Если жидкость неподвижна, а скорость движения тела невелика, то перемещение тела не оказывает влияния на удалённые слои жидкости. Взаимодействие происходит только со слоем, непосредственно соприкасающимся с телом. При движении пружинного маятника в вязкой среде, с небольшими скоростями сила сопротивления пропорциональна скорости движения
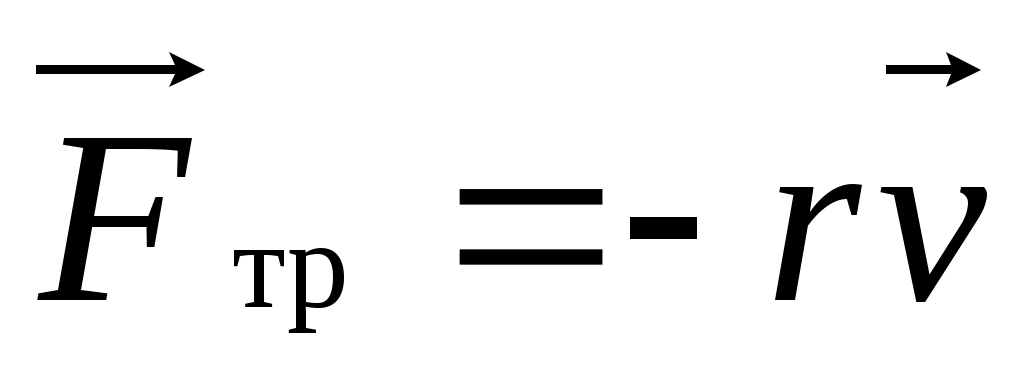 , (10.5) , (10.5)
где коэффициент r зависит от вязкости среды и площади соприкосновения поверхности S тела с жидкостью,
 r r ηS, (10.6)
где η – коэффициент внутреннего трения жидкости (динамическая вязкость жидкости)
Дж. Стокс эмпирически установил, что для тел сферической формы радиуса R коэффициент сопротивления равен 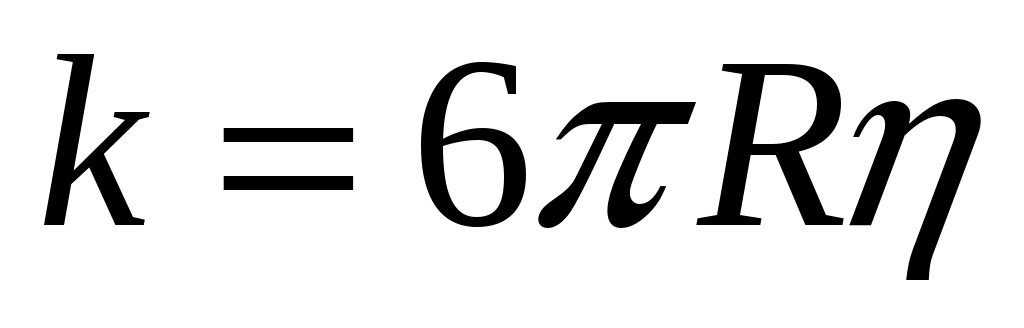 . Следовательно, сила сопротивления среды равна: . Следовательно, сила сопротивления среды равна:
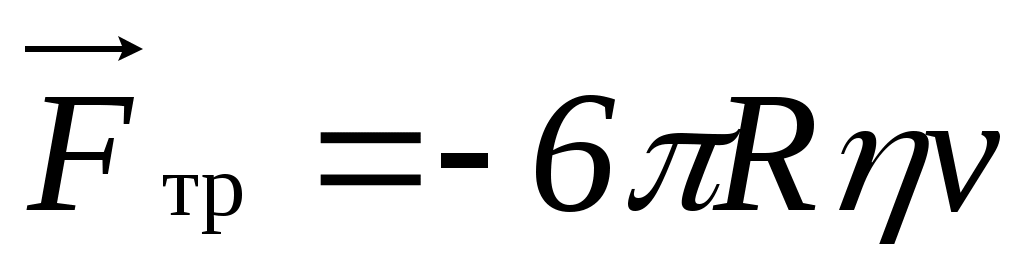 . (10.7) . (10.7)
При равномерном движении сферы в идеальной (не вязкой) жидкости, она не испытывает никакого сопротивления. Выводы Стокса для сферы верны также для эллипсоида вращения и других тел с подобными поверхностями. Сила Архимеда, действующая, на груз и направленная в одну и ту же сторону, будет скомпенсирована некоторым начальным растяжением пружины, Δl в дальнейшем рассмотрении участвовать не будет.
Для описания движения груза пружинного маятника в вязкой среде необходимо в правую часть уравнения (10.1) включить величину силы трения (10.5). Поэтому свободные колебания будут затухающими (следовательно, не гармоническими). В результате второй закон динамики для механического осциллятора при наличии вязкого трения можно записать так:
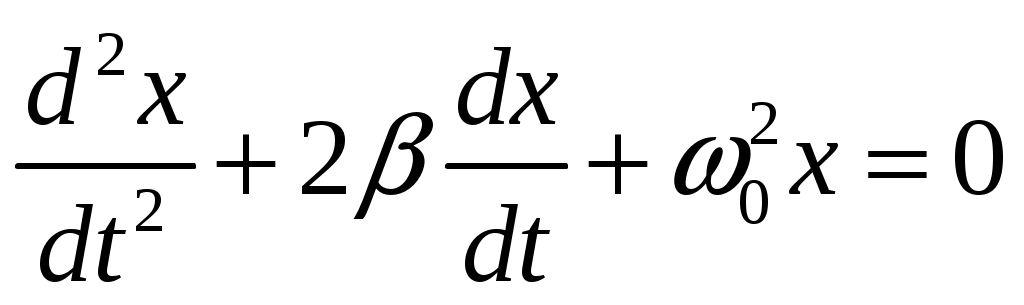 , (10.8) , (10.8)
где  – коэффициент затухания; – коэффициент затухания; 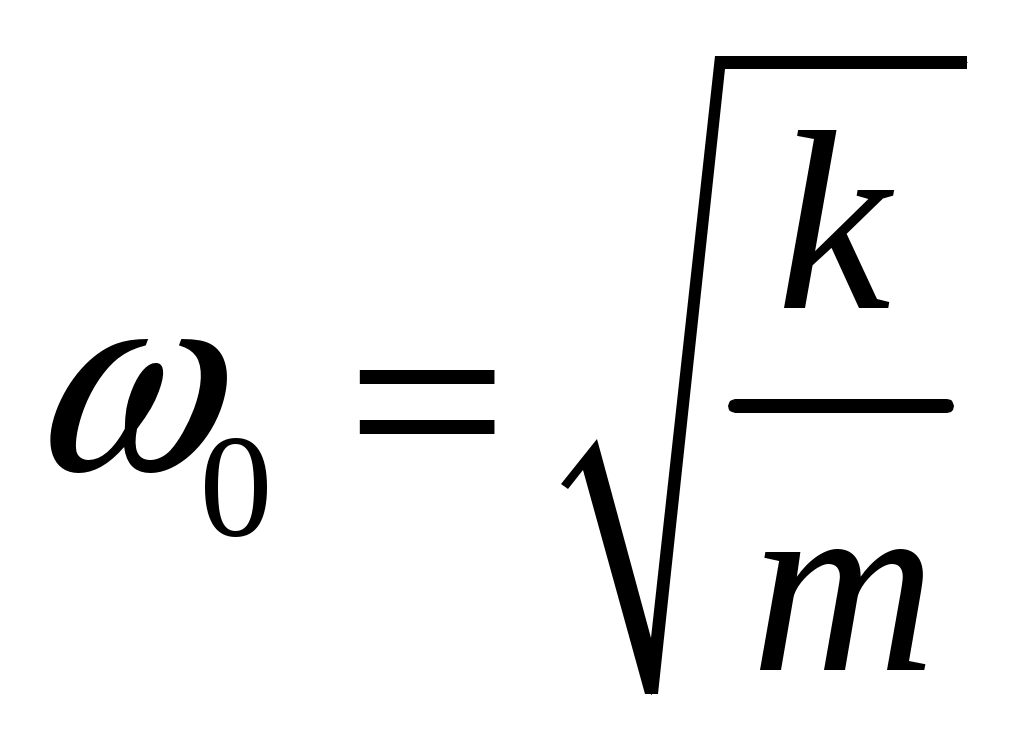 – собственная частота незатухающих колебаний. – собственная частота незатухающих колебаний.
Можно показать, что решением этого уравнения является функция
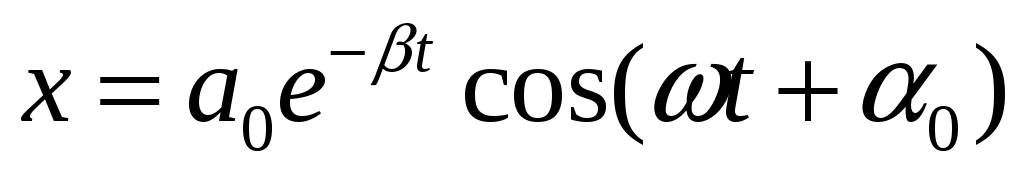 , (10.9) , (10.9)
где  - частота затухающих колебаний. - частота затухающих колебаний.
Отношение двух соседних амплитуд 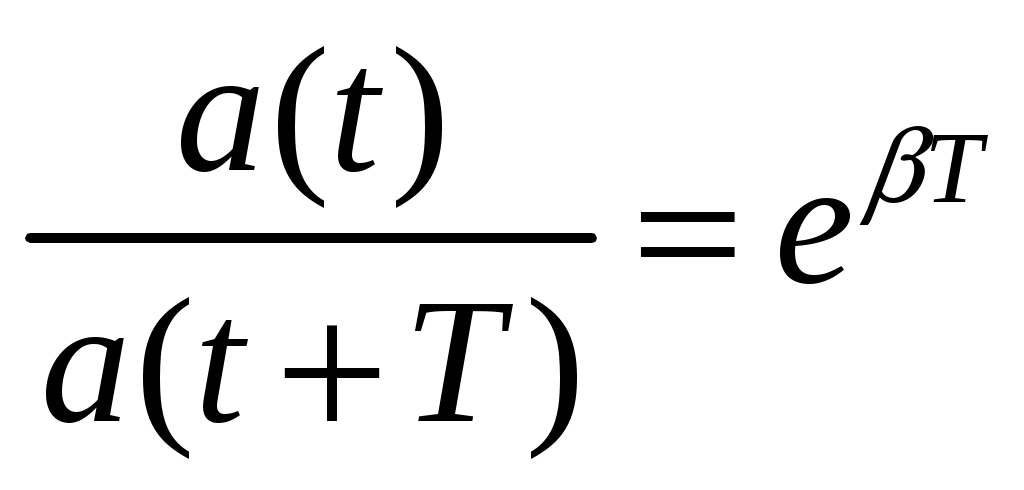 называется декрементом затухания. называется декрементом затухания.
Величина 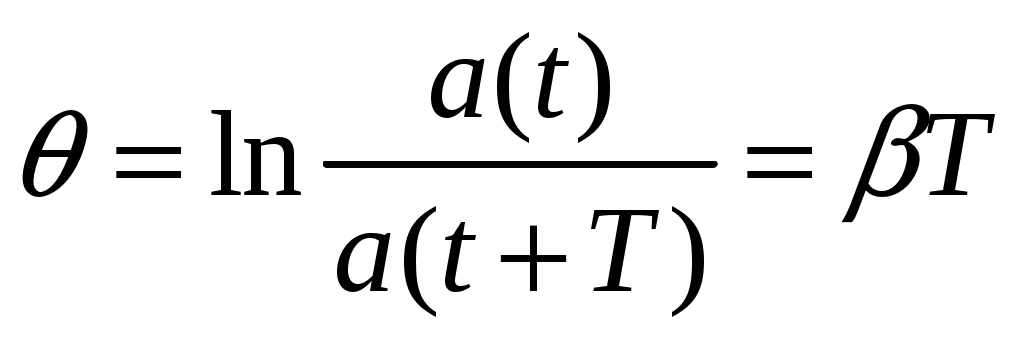 называется логарифмическим декрементом затухания. называется логарифмическим декрементом затухания.
По истечении N колебаний эта величина определяется по формуле
 . (10.10) . (10.10)
Энергия пружинного маятника пропорциональна квадрату амплитуды колебаний:
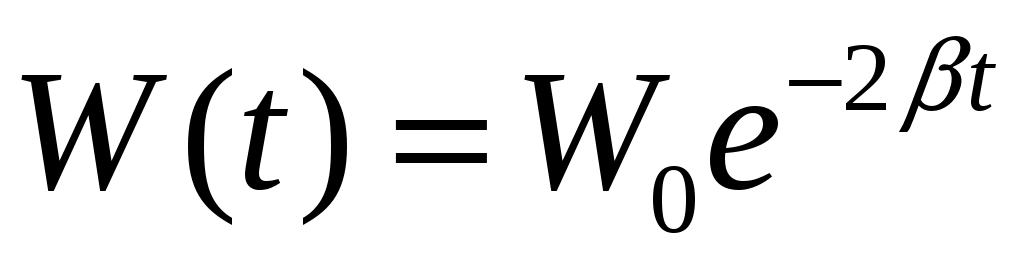 , (10.11) , (10.11)
где  – энергия пружины при максимальной начальной амплитуде, то есть начальный запас энергии пружинного маятника. – энергия пружины при максимальной начальной амплитуде, то есть начальный запас энергии пружинного маятника.
Потеря энергии маятника за период равна:
 . (10.12) . (10.12)
Из (10.10) и (10.11) следует
 . (10.13) . (10.13)
При малых затуханиях  и соотношение (10.12) можно преобразовать к виду и соотношение (10.12) можно преобразовать к виду
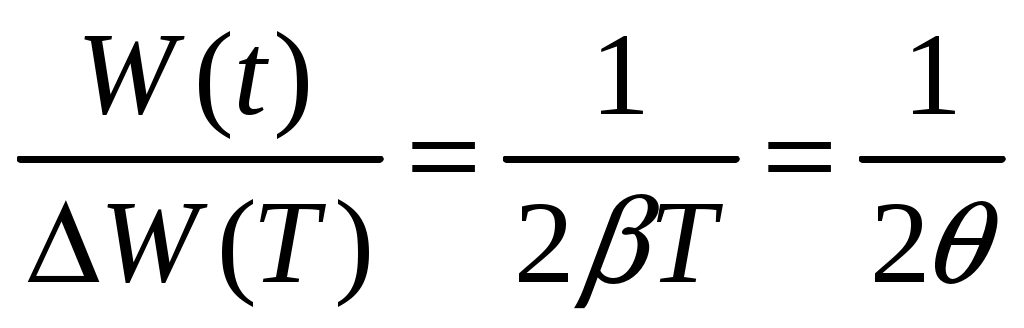 . (10.14) . (10.14)
Описание схемы установки
На Рис. 10.2 представлена схема установки. На платформе 1 расположены стойка 3, к которой подвешена пружина 8, стеклянный цилиндр с жидкостью 4 секундомер 2 для отсчёта числа колебаний на установленные интервалы времени, инфракрасный датчик 9 для фиксирования флажка 7, закреплённого на штоке 6 , при прохождении луча датчика. На конце штока 6 крепятся сменные грузы - металлический шар или эллипсоид одинаковой массы. Для вертикальной установки системы (пружина, груз) служит отвес 10. Длина пружины без груза 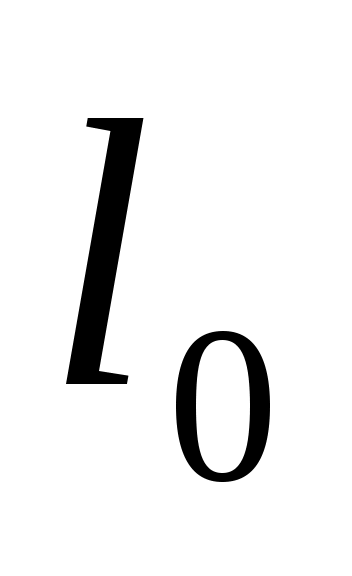 , величина удлинения пружины , величина удлинения пружины  с подвешенным к ней грузом, начальное отклонение груза α0(0) и амплитуда по истечении времени α(t) фиксируется флажком 7 на шкале 11. с подвешенным к ней грузом, начальное отклонение груза α0(0) и амплитуда по истечении времени α(t) фиксируется флажком 7 на шкале 11.
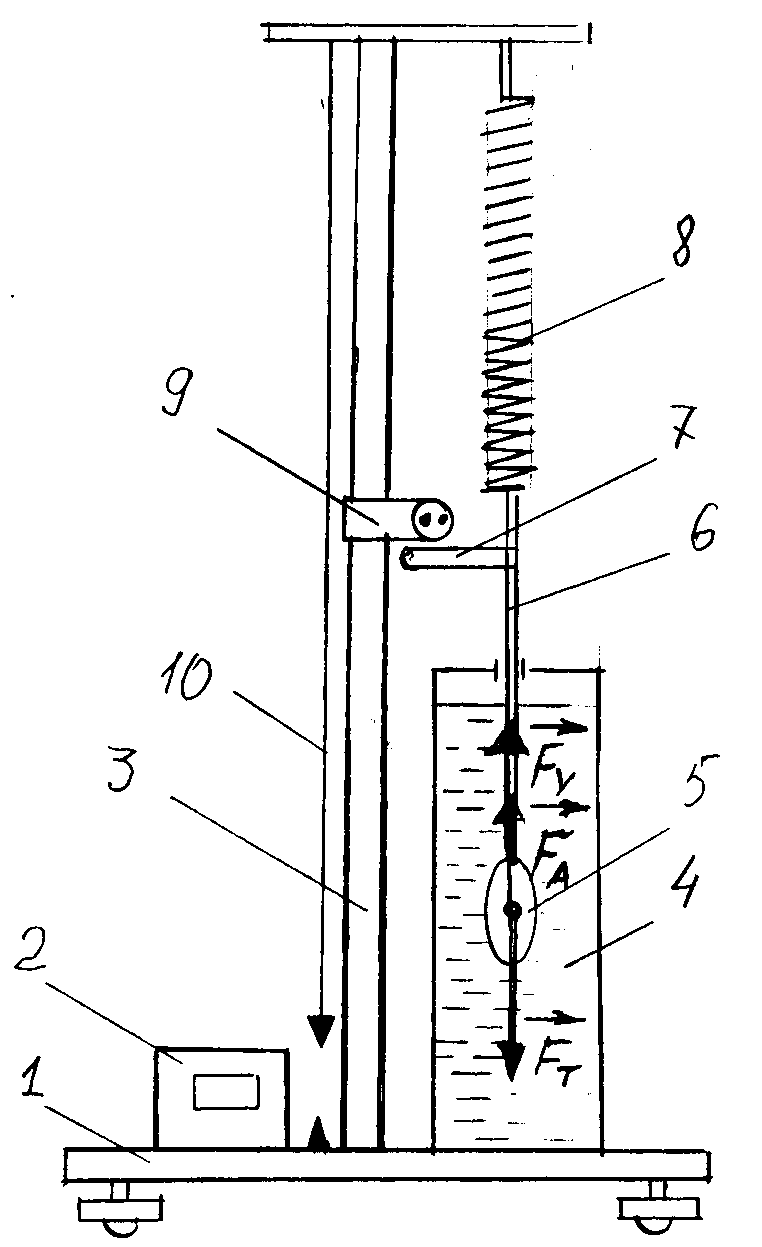 
Рис. 10.2
Для проведения опытов необходимы следующие средства измерений.
Электронный секундомер с точностью отсчёта ± 0,01 с для измерения времени и установленного числа колебаний груза. В установке используется программируемый электронный секундомер, измеряющий время установленного числа колебаний.
Линейка с миллиметровой шкалой для измерений смещений груза по вертикали.
Порядок выполнения работы
1. Проверить с помощью отвеса 10 вертикальное положение стойки 3.
2. Измерить длину пружины без груза 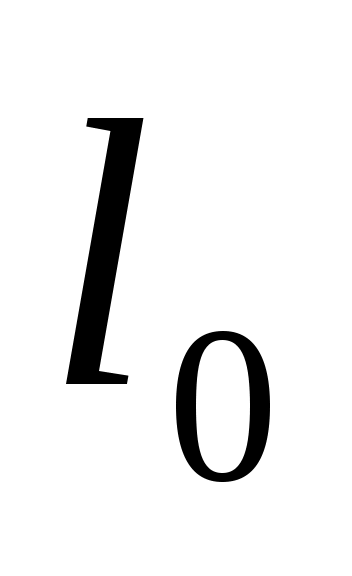 , отсчитав положения её первого и последнего витка по миллиметровой шкале. , отсчитав положения её первого и последнего витка по миллиметровой шкале.
3. Закрепить на конце пружины груз (металлический шар известной массы), поместить систему в стеклянный цилиндр с жидкостью и измерить длину пружины с грузом  , отсчитав положения её первого и последнего витка по миллиметровой шкале. , отсчитав положения её первого и последнего витка по миллиметровой шкале.
4. С помощью штока 6 переместить груз вертикально вниз, зафиксировать его положение зажимом 12, и по флажку 7 отсчитать на миллиметровой шкале 11 начальное отклонение груза α0(0) от положения равновесия.
5. Включить секундомер 2 и привести в движение маятник.
6. По истечении установленного числа колебаний произвести отсчёт амплитуды последнего колебания α(t) флажком 7 на шкале 11.
7. Снять показания электронного секундомера времени установленного числа колебаний N.
8. Для статистической обработки измеренных величин пункты 6 и 7 повторить не менее 5 раз.
9. Пункты 2–8 повторить для двух грузов – шара и эллипсоида.
Обработка результатов измерений
1. По формуле (10.10) определить величину логарифмического декремента затухания.
2. Из соотношения определить коэффициент затухания определить коэффициент затухания 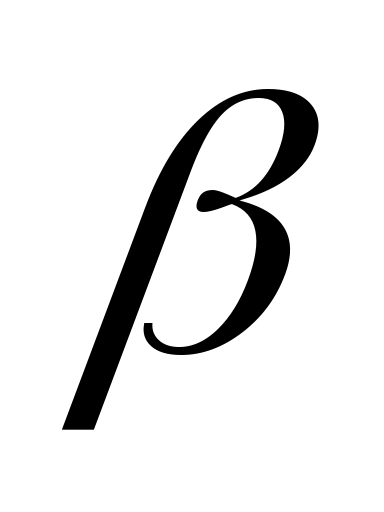 . .
3. Определить коэффициент сопротивления для шара и эллипсоида 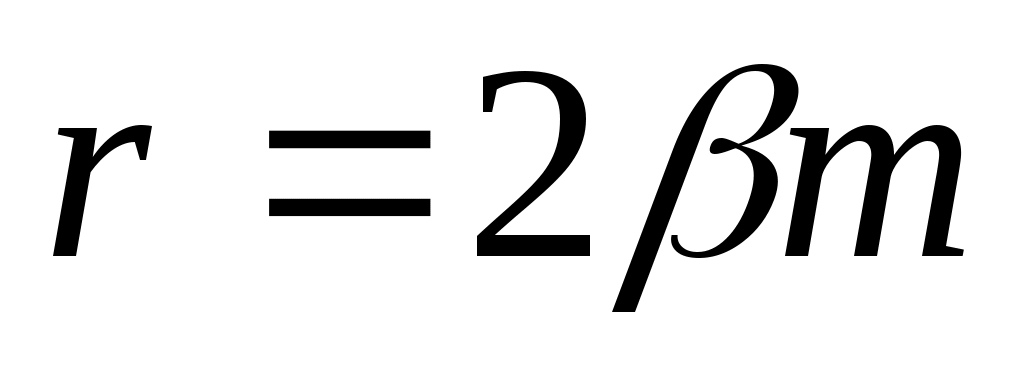 . .
4. По формуле (10.14) определить относительную величину потери энергии пружинного маятника.
Контрольные вопросы
1. Дайте определение колебательного процесса.
2. Запишите уравнение гармонических колебаний.
3. Что называется амплитудой, периодом, частотой (круговой или циклической) и фазой колебания.
4. Запишите уравнение затухающих колебаний.
5. Дайте определение логарифмического декремента затухания, добротности колебательной системы.
6. Запишите уравнение свободных колебаний пружинного маятника.
Лабораторная работа №2
СОБСТВЕННЫЕ КОЛЕБАНИЯ СИСТЕМЫ С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
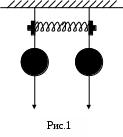
Два маятника, связанных легкой пружиной (рис.1), могущих давать колебания только в вертикальной плоскости, проходящей через точки подвеса, являются системой с двумя степенями свободы.
При возбуждении колебаний в системе можно заметить, что амплитуды каждого из маятников обнаруживают медленное периодическое изменение, так называемое биение. При этом в соответствии с законом сохранения энергии в тот момент, когда амплитуда одного из маятников достигает максимума, амплитуда второго маятника имеет минимум, и наоборот. Смещение маятников от положения равновесия графически представлены на рис.2. Для того чтобы разобраться в картине биений, рассмотрим вопрос о сложении гармонических колебаний, происходящих в одном направлении.
Пусть точка содержит колебания относительно какой-то системы отсчета в направлении оси х.
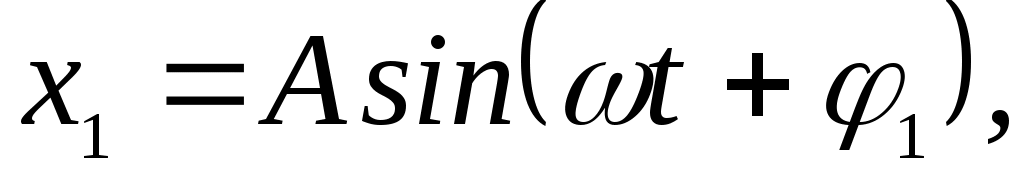
а сама система отсчета совершает колебания в том же направлении

тогда колебания точки относительно неподвижной системы отсчета будут
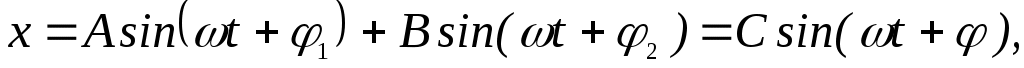
где

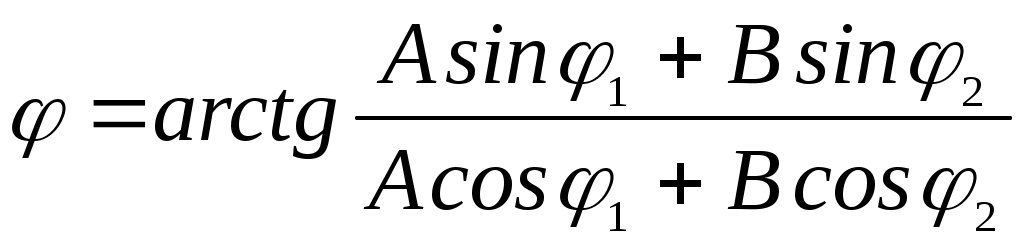
φ1 и φ2 –начальные фазы колебания;
А, В, С – амплитуды колебаний;
ω – круговая частота;
t – время.
Колебание, полученное при этом, гармоническое (т.е. совершается по закону синуса или косинуса).
Колебание, полученное при сложении двух гармонических колебаний, имеющих одно направление, но различные частоты, представляет иную картину: оно не будет гармоническим.
Пусть


тогда результирующее суммарное колебание

или

Первое слагаемое не является гармоническим колебанием, оно представляет произведение двух гармонических сомножителей с частотами ½(ω1-ω2) и ½(ω1+ω2).
Если ω1 и ω2 близки, то ½(ω1+ω2) одного порядка с ω1 и ω2, а частоты ½(ω1-ω2) будет по сравнению с ω1 и ω2 очень малой. В этом случае, когда ½(ω1-ω2)<<ω1 (или ω2), первое слагаемое результирующего колебания можно представить себе как почти гармоническое колебание с частотой ω1 (или ω2), у которого амплитуда, равная 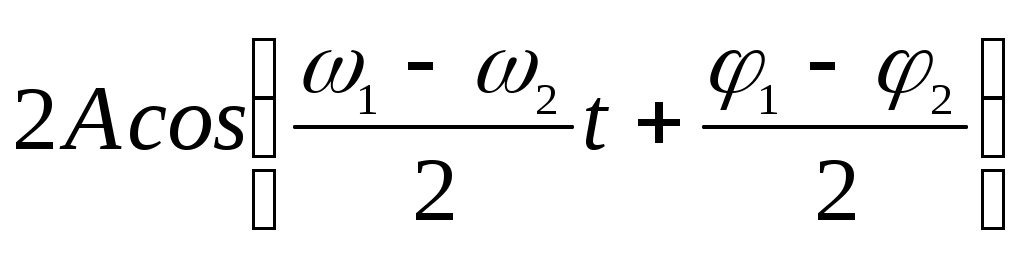 , медленно изменяется со временем. График таких колебаний будет совпадать с тем, что показано на рисунке 2. Их можно назвать «чистыми биениями». , медленно изменяется со временем. График таких колебаний будет совпадать с тем, что показано на рисунке 2. Их можно назвать «чистыми биениями».
Период биения 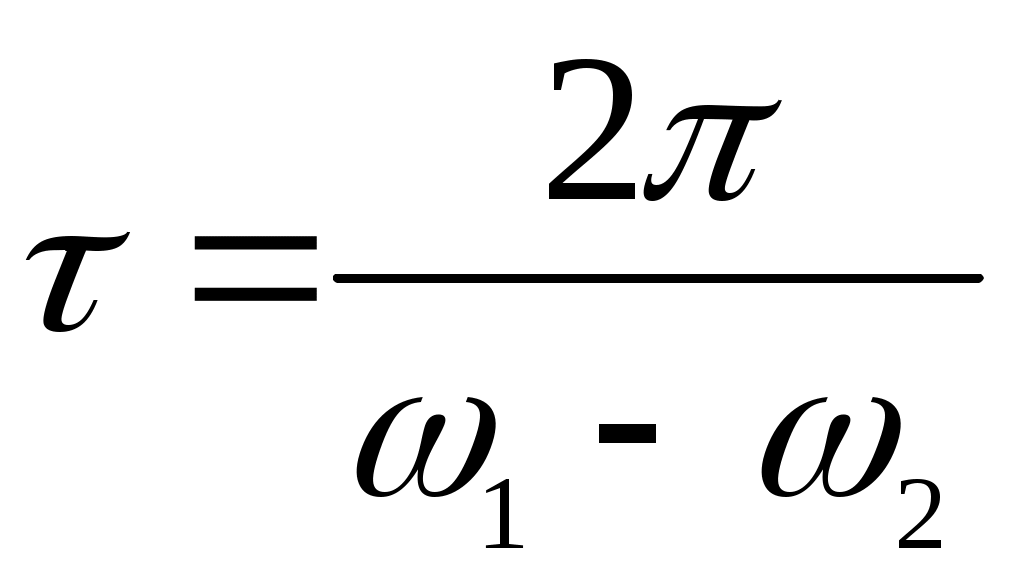 (через такой период повторяются значения cos, знак не учитывается), второе слагаемое уравнения (1) представляет собой гармонические колебания с частотой ω2, сложение биений с гармоническими колебаниями дает картину биений, при которых «амплитуда» колебаний будет изменяться с периодом биений τ, но никогда не достигнет нуля (рис.3), амплитуды А≠В, то есть будут обычные биения с частотой (через такой период повторяются значения cos, знак не учитывается), второе слагаемое уравнения (1) представляет собой гармонические колебания с частотой ω2, сложение биений с гармоническими колебаниями дает картину биений, при которых «амплитуда» колебаний будет изменяться с периодом биений τ, но никогда не достигнет нуля (рис.3), амплитуды А≠В, то есть будут обычные биения с частотой

Сравнивая результаты теоретического анализа сложения двух гармонических колебаний различной частоты с колебаниями связанных маятников, мы приходим к заключению, что собственные колебания двух маятников состоит из суммы двух гармонических колебаний, причем разность частот этих колебаний равна частоте биений.
Анализ колебаний системы связанных маятников показывает, что можно подобрать такие условия, при которых колебания происходят только с одной из собственных частот колебаний системы ν1 или ν2. В этом случае биений не будет.

ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ
1. Пружину снимают с маятников, их чечевицы ставят в одинаковое положение и затем определяют периоды колебаний того и другого маятника в отдельности, измеряя по секундомеру промежуток времени, в течение которого маятник совершает 5-10 колебаний.
Периоды колебаний обеих маятников должны измеряться с точностью до 0,01 сек. Если периоды оказываются различными, необходимо добиться их равенства, постепенно передвигая чечевицу одного из маятников.
2. Накладывают на маятник пружину «а», устанавливают его на середину верхней части штанги и приводят маятник в колебание при произвольных начальных условиях. Из наблюдений определяют νδ биений, измеряя по секундомеру промежуток времени, который протекает между двумя последовательными максимумами (или минимумами) амплитуд одного и того же маятника. Следует убедиться, что частота биений не зависит от начальных условий, т.е. от углов начального отклонения того и другого маятника.
3. Вызывая колебания при начальных условиях, соответствующих рисункам 4а и б, следует убедиться в отсутствии биения в этих случаях. Одновременно определить периоды колебаний в первом (а) и во втором (б) случаях. Сравните разность полученных частот ν1 и ν2 и с частотой νδ, измеренной в опыте 2.
Должно выполняться равенство
ν1-ν2=νδ
Отсутствия биения указывает на то, что амплитуда колебаний одной из собственных частот равна нулю и маятники совершают колебания с одной из собственных частот ν1 и ν2. Следовательно, ν1 и ν2 – собственные частоты маятников.
4. Остановив один из маятников, приводят другой в колебание и наблюдают полную передачу энергии, измеряя по секундомеру частоту этого процесса.
5. Определите периоды колебаний каждого из маятников в этом случае, когда один из них закреплен, а другой совершает колебаний. (При той же связи, что и в опыте 3). Данные внести в таблицу 1.
6. Измените, период колебаний одного маятника и проверьте, будут ли биения при колебаниях в системе с начальными условиями, указанными в пункте 3.
Таблица 1
№опыта
|
Число колебаний
|
Время (сек)
|
Период
|
1-й маят.
|
2-й маят.
|
1-й маят.
|
2-й маят.
|
без пружины
|
|
|
|
|
|
с пружиной
|
|
|
|
|
|
Упр.№1
Таблица 2
Определение часто ты биений
№ п/п измер.
|
Число биений
|
Время (сек)
|
Период биений
|
Частота биений
|
Ошибка
|
|
|
|
|
|
|
Упр.№2
Таблица 2
Определение частоты колебаний маятников, когда они колеблются в одинаковых фазах
№ п/п измер.
|
Число биений
|
Время колебаний
|
Период колебаний
|
Частота колебаний
|
Ошибка
|
|
|
|
|
|
|
Упр.№3
Таблица 4
Определение частоты колебаний маятников, когда они колеблются в противоположных фазах
№ п/п измер.
|
Число колебаний
|
Время колебаний
|
Период колебаний
|
Частота колебаний
|
Ошибка
|
|
|
|
|
|
|
Контрольные вопросы
1. При сложении, каких колебаний получаются биения? Укажите, когда получаются «чистые биения».
2. От чего зависят собственные частоты связанных колебаний?
3. Нарисуйте график зависимости энергии от времени в системе каждого маятника и всей системы.
4. При каких условиях в системе нет биений?
5. Как влияет связь на частоту биения, от чего зависит сама связь?
6. При каких начальных условиях частота колебаний больше – в случае а и б (задача 3)? Почему?
7. Сколько нормальных колебаний имеет связанная система?
8. Как с помощью нормальных колебаний представляется произвольное колебание связанной системы?
Лабораторная работа №3
ОПРЕДЕЛЕНИЕ ЧАСТОТЫ КОЛЕБАНИЙ МЕТОДОМ РЕЗОНАНСА
Цель работы: определение частоты колебаний камертона и скорости звука в воздухе.
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Если в каком-либо месте упругой (твердой, жидкой или газообразной) среды возбудить колебания ее частиц, то вследствие взаимодействия между частицами это колебание начнет распространяться в среде от частицы к частице с некоторой скоростью V. Процесс распространения колебаний в пространстве называется волной.
Частицы среды, в которой распространяется волна, не переносятся волной — они лишь совершают колебания около своих положений равновесия. В зависимости от направления колебаний частиц по отношению к направлению, в котором распространяется волна, различают продольные и поперечные волны, В продольной волне частицы среды колеблются вдоль направления распространения волны. В поперечной волне частицы среды колеблются в направлениях, перпендикулярных к направлению распространения волны. Механические поперечные волны могут возникнуть лишь в среде, обладающей сопротивлением сдвигу. Поэтому в жидкой и газообразной средах возможно возникновение только продольных волн. В твердой среде возможно возникновение как продольных, так и поперечных воли.
Распространяясь от источника колебаний, волновой процесс охватывает все новые и новые части пространства. Геометрическое место точек, до которых доходят колебания к моменту времени t, называется фронтом волны.
Если в среде распространяется одновременно несколько волн, то колебания частиц среды геометрически складываются из суммы колебаний, которые совершали бы частицы при распространении каждой из волн в отдельности. Следовательно, волны просто накладываются одна на другую, не возмущая друг друга.
В случае, когда колебания, обусловленные отдельными волнами в каждой из точек среды, обладают постоянной разностью фаз, волны называются когерентными.
При сложении когерентных волн возникает явление интерференции, заключающееся в том, что колебания в одних точках усиливают, а в других точках ослабляют друг друга.
Очень важный случай интерференции наблюдается при наложении двух встречных плоских волн с одинаковой амплитудой. Возникающий в результате колебательный процесс называется стоячей волной. Практически стоячие волны возникают при отражении волн от преград. Падающая на преграду волна и бегущая ей навстречу отраженная, накладываясь одна на другую, образуют стоячую волну.
Уравнения двух плоских волн, распространяющихся в противоположных направлениях, имеют вид:
 (1) (1)
Складывая оба уравнения и преобразовывая результат по формуле для суммы косинусов, получаем:
 (2) (2)
Заменив волновое число k его значением 2π/λ, выражению для ξ можно придать следующий вид:
 (3) (3)
Величина ξ представляет собой смещение любой из точек с координатой х в момент времени t.
Уравнение (3) и есть уравнение стоячей волны. Из него видно, что в каждой точке стоячей волны происходят колебания той же частоты, что и у встречных волн, причем амплитуда А оказывается зависящей от х:
 . .
Амплитуда колебаний достигает максимального значения 2а в точках, где выполняется условие:
2πx/λ=±nπ, (4)
где n = 0,1,2
Эти точки называются пучностями стоячей волны. Из условия (4) получаем значения координат пучностей:
xпучн=±nλ/2 (5)
В точках, где выполняется условие
2πx/λ=±(n+1/2)π,
а мплитуда колебаний обращается в нуль. Эти точки называются узлами стоячей волны. Точки среды, находящиеся в узлах, колебаний не совершают. Координаты узлов имеют следующие значения: мплитуда колебаний обращается в нуль. Эти точки называются узлами стоячей волны. Точки среды, находящиеся в узлах, колебаний не совершают. Координаты узлов имеют следующие значения:
xузл=±(n+1/2)λ/2. (6)
И
Рис.1
з формул (5) и (6) следует, что расстояние между соседними пучностями, так же как и расстояние между соседними узлами, равно λ/2. Пучности и узлы сдвинуты друг относительно друга на четверть длины волны (рис.1).
Расстояние между ближайшими частицами, колеблющимися одинаковым образом (в одинаковой фазе), называется длиной волны λ. Длина волны очевидно равна тому расстоянию, на которое распространяется волна за период Т:
λ = VT.
ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ
Описание установки
Н а рисунке 2 изображен прибор Квинке, используемый в данной работе. Столб воздуха, необходимый для возникновения стоячих волн, заключен в трубке А, изменение длины столба воздуха производится поднятием сосуда Д. а рисунке 2 изображен прибор Квинке, используемый в данной работе. Столб воздуха, необходимый для возникновения стоячих волн, заключен в трубке А, изменение длины столба воздуха производится поднятием сосуда Д.
Камертон, частоту колебаний которого желают определить, укрепляется так, что его ножки расположены к оси трубы вблизи ее открытого конца (но не слишком близко, чтобы при ударе молоточком камертон не ударялся о трубку А). Звук вызывается ударами резинового молоточка. Возникновение стоячей волны сопровождается резким усилением звука. Столб ВС (рис.2) в этом случае можно рассматривать как вибратор, частота собственных колебаний которого совпадает с частотой источника звуковых колебаний, благодаря чему он резонирует и усиливает звук. Это дает возможность найти положения a, b, c и определить длину волны.
Зная скорость звука при данной температуре, которая определяется из соотношения
   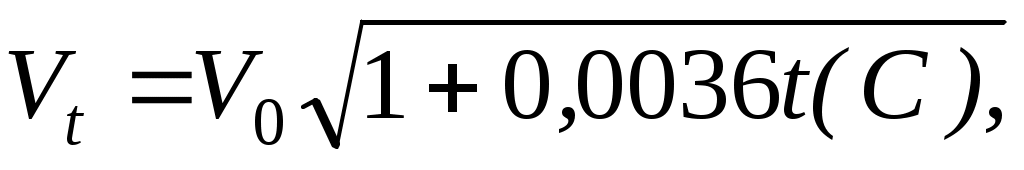
и длину волны при данной температуре, мы можем определить частоту колебаний источника звука — камертона (V0= 332 м/с — скорость звука в воздухе при 0 °С).
Проведение эксперимента
1. Проверив установку, привести камертон в состояние колебания и, медленно повышая уровень воды, отметить положение, когда звук достигнет максимальной силы.
2. Отодвигая далее уровень воды, найти второй максимум. Расстояние между этими положениями будет равно половине длины волны λ/2.
З. Если трубка А достаточно длинна, то можно найти и третье положение уровня, при котором звук достигает максимальной силы. Установка уровня производится несколько раз. Все полученные результаты заносятся в таблицу 1.
4. Определяется средняя величина λ и погрешности.
5. По формуле v=Vt/λ вычисляется частота колебаний камертона.
Таблица 1
№уровня
|
Положение уровня, х
|
λ, см
|
Vt ,м/с
|
 , Гц , Гц
|
х1, см
|
х2, см
|
х3, см
|
<х>, см
|
1
|
|
|
|
|
|
|
|
2
|
|
|
|
|
|
|
|
3
|
|
|
|
|
|
|
|
Контрольные вопросы.
1. Что называется резонансом?
2. В чем заключается причина возникновения стоячих волн?
3. Почему стоячая волна не переносит энергии?
4. Как в данном опыте изменяется фаза звуковой волны при отражении от поверхности?
5. Покажите, что расстояние между двумя соседними пучностями равно λ/2.
6. Каковы основные причины, вызывающие погрешности измерения на данной установке?
7. Можно ли для проведения опыта брать источник, дающий не звук, а шум?
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Савельев И.В. Курс физики в З т. Т.1. Механика. Молекулярная физика. М.: Наука. 1989. 432с.
2. Геворкяя Р.Г. Курс физики. М.: Высшая школа. 1979. 656с.
3. Детлаф А.А., Яворский БМ. Курс физики. М.: Высшая школа. 1989. 608с. 4. Каленков С.Г., Соломахо Г.И. Практикум по физике. Механика. М.: Высшая школа. 1990. 11 Iс.
5. Деденко Л.Г., Киселев Д.Ф., Петерсон В.К., Слепков А.И. Общий физический практикум. Механика. М.: Изд-во МГУ. 1991. 272с.
6. Виноградов Ю.К., Котельников ВА., Студников Е.Л. и др. Практикум по физике. Электричество и магнетизм. М.: Высшая школа. 1991. 151с.
Лабораторная работа №4
Явление резонанса в колебательном контуре
Цель работы: изучение резонанса в последовательном колебательном контуре, определение резонансной частоты колебаний и добротности колебательного контура.
|
 Скачать 0.55 Mb.
Скачать 0.55 Mb. мплитуда колебаний обращается в нуль. Эти точки называются узлами стоячей волны. Точки среды, находящиеся в узлах, колебаний не совершают. Координаты узлов имеют следующие значения:
мплитуда колебаний обращается в нуль. Эти точки называются узлами стоячей волны. Точки среды, находящиеся в узлах, колебаний не совершают. Координаты узлов имеют следующие значения:  а рисунке 2 изображен прибор Квинке, используемый в данной работе. Столб воздуха, необходимый для возникновения стоячих волн, заключен в трубке А, изменение длины столба воздуха производится поднятием сосуда Д.
а рисунке 2 изображен прибор Квинке, используемый в данной работе. Столб воздуха, необходимый для возникновения стоячих волн, заключен в трубке А, изменение длины столба воздуха производится поднятием сосуда Д. 






