Лабораторная работа 1 изучение затухающих механических колебаний пружинного маятника цель работы
 Скачать 0.55 Mb. Скачать 0.55 Mb.
|
1 2 ТЕОРЕТИЧЕСКАЯ ЧАСТЬС 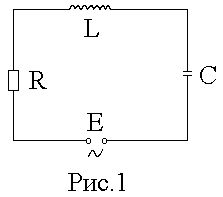 обственные колебания происходят в изолированной системе после подействовавшего на нее внешнего возмущения. Название собственные колебания означает, что процесс колебаний в этом случае определяется свойствами самой системы. Энергия колебаний доставляется системе извне в начальный момент возбуждения колебаний. Если энергия постоянно подводится к системе, то колебания, возникающие в ней, называются вынужденными. Электромагнитные колебания изучаются с помощью колебательного контура, состоящего из конденсатора C, катушки индуктивности L и активного сопротивления R. Различают последовательный (рис.1) и параллельный (рис.2) колебательные контуры. обственные колебания происходят в изолированной системе после подействовавшего на нее внешнего возмущения. Название собственные колебания означает, что процесс колебаний в этом случае определяется свойствами самой системы. Энергия колебаний доставляется системе извне в начальный момент возбуждения колебаний. Если энергия постоянно подводится к системе, то колебания, возникающие в ней, называются вынужденными. Электромагнитные колебания изучаются с помощью колебательного контура, состоящего из конденсатора C, катушки индуктивности L и активного сопротивления R. Различают последовательный (рис.1) и параллельный (рис.2) колебательные контуры.Р 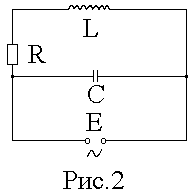 ассмотрим процесс собственных колебаний. Начальные условия, при которых возникают собственные колебания, определяют начальную фазу процесса и амплитуду колебаний. Процесс электромагнитных колнбаний в контуре заключается в периодической перезарядке конденсатора и в протекании переменного тока в цепи, замыкающей пластины конденсатора. При этом электростатическая энергия поля заряженного конденсатора переходит в энергию магнитного поля тока, протекающего через катушку индуктивности, и обратно. Из-за активного сопротивления, имеющегося в реальном контуре (провода и т.п.), разряд конденсатора не является абсолютно периодическим процессом. Амплитуда напряжения на конденсаторе после каждой его перезарядки становится все меньше; амплитуда тока тоже убывает. В дальнейшем мы будем изучать последовательный колебательный контур. ассмотрим процесс собственных колебаний. Начальные условия, при которых возникают собственные колебания, определяют начальную фазу процесса и амплитуду колебаний. Процесс электромагнитных колнбаний в контуре заключается в периодической перезарядке конденсатора и в протекании переменного тока в цепи, замыкающей пластины конденсатора. При этом электростатическая энергия поля заряженного конденсатора переходит в энергию магнитного поля тока, протекающего через катушку индуктивности, и обратно. Из-за активного сопротивления, имеющегося в реальном контуре (провода и т.п.), разряд конденсатора не является абсолютно периодическим процессом. Амплитуда напряжения на конденсаторе после каждой его перезарядки становится все меньше; амплитуда тока тоже убывает. В дальнейшем мы будем изучать последовательный колебательный контур.Ток, текущий в колебательном контуре, считается квазистационарным, т.е. таким, когда во всех элементах последовательной электрической цепи его значение в данный момент одинаково. Мгновенное значение напряжения на конденсаторе такое же, как и при тех же, но неизменных во времени зарядах на его пластинах. Для мгновенных значений квазистационарных токов справедливы законы, установленные для цепей постоянного тока. Внешняя электродвижущая сила создает в цепи переменное напряжение, изменяющееся по косинусоидальному закону: E = Eocos(wt), (1) где t - время, Ео - э.д.с. в начальный момент времени, w = 2pu – круговая частота, u - частота. Сила тока в контуре I связана с зарядом Q и разностью потенциалов U на конденсаторе соотношением I = где Q = CU есть заряд конденсатора; знак минус указывает на то, что положительным мы считаем то направление тока, которое соответствует убыли разности потенциалов на пластинах конденсатора. Изменение силы тока во времени вызывает электродвижущую силу самоиндукции в катушке, равную Ec = - L Из закона Ома следует U + Ec - IR = E. Подставляя в это уравнение формулы (1), (2) и (3), получим U + LC Разделим уравнение (4) на LC и введем обозначения(wo)2 = 1/(LC), b = R/(2L). После преобразований получим дифференциальное уравнение, являющееся уравнением колебательного контура: При отсутствии внешней электродвижущей силы Уравнение (6) есть уравнение собственных колебаний в контуре. Его решение будет иметь вид: U = U0e-btcos(wot + jo) (7) где U0 и jo - константы, зависящие от начальных условий. Для идеального контура ( R = b = 0 ) уравнение (6) упрощается и его решение в этом случае U = U0cos(wot + jo), (7a) где w0 = 1/(LC) - собственная частота идеального контура. Формула (7) описывает затухающие гармонические колебания с периодом Если R достаточно мало по сравнению с L (контур близок к идеальному), то получим формулу 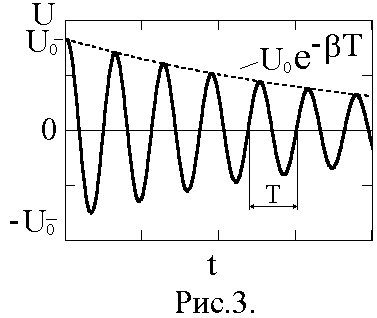 To º To º определяющую период колебаний в контуре без затухания (формула Томпсона). Формулы (7) и (7a) определяют зависимости U(t) при затухающих и незатухающих колебаниях (рис.3). Величина b, определяющая степень затухания, называется коэффициентом затухания. На практике вместо нее обычно используется другая мера затухания, называемая логарифмическим декрементом затухания g: g º ln где Un и Un+1 - величины двух последовательных амплитуд, отстающих друг от друга на один период. Т.к. Un+1 = Une-bT, то g = ln(Un/Un+1) = bT = (R/(2L))T. Логарифмический декремент затухания связан с числом полных колебаний N, совершаемых за время t, зависимостью g = bT = Величина Q = pN называется добротностью колебательного контура. При малом затухании (b2 << w02) добротность можно вычислить по формуле: Q = pN = Отсюда следует, что чем меньше R и чем больше L, тем меньше затухание, тем ближе кривая (7) к синусоиде (7a). При значительном возрастании R затухание, так же как и период, увеличивается. Начиная с R = 2 В настоящей работе исследуются вынужденные колебания в последовательном колебательном контуре, соединенном с источником электродвижущей силы переменной частоты. Вынужденные колебанияДифференциальное уравнение (5) описывает процесс изменения напряжения на конденсаторе колебательного контура при наличии омического сопротивления и внешней косинусоидальной периодической электродвижущей силы. Его решение можно представить как сумму общего решения однородного уравнения (6) и частного решения уравнения (5). Общее решение уравнения (5) - уравнение затухающих колебаний. При t >> t = 1/b эта часть решения исчезнет; следовательно, она отражает переходный процесс, определенный начальными условиями и параметрами контура. Не зависящие от начальных условий установившиеся колебания в цепи определяются частным решением, которое ищем в виде U = Uo cos (wt - j ), (10) где Uo и j подлежат определению. После подстановки (10) в (5) получим -Uow2cos(wt-j)-2bUowsin(wt-j)+wo2Uocos(wt-j)=Eowo2cos(wt). (11) Равенство (11) должно сохраняться в любой момент времени t. При wt = p/2 уравнение (11) переходит в -Uow2sin(j)-2bUowcos(j)+wo2Uosin(j)=0, откуда tgj = 2bw/(wo2 - b2). (12) При wt = 0 получим соотношение -Uow2cosj + 2bwUosinj + wo2Uocosj = Eo2wo2, позволяющее после несложных преобразований отыскать амплитуду установившихся колебаний: Uo = 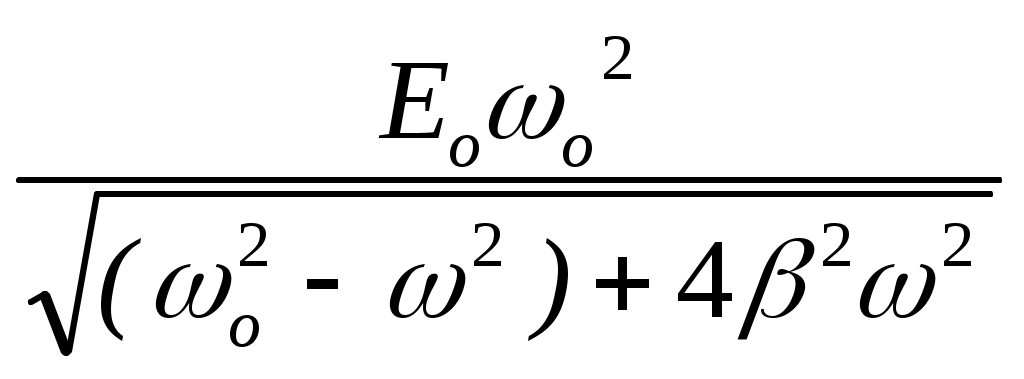 . (13) . (13)При найденных значениях амплитуды Uo и фазы j уравнение (10) представляет собой зависимость напряжения на конденсаторе колебательного контура при вынужденных колебаниях от времени. Сила тока в контуре равна I = -C где j1 = p/2 + j - разность фаз между силой тока и приложенным к контуру напряжением. Амплитуда силы тока в контуре равна I0 = CU0W или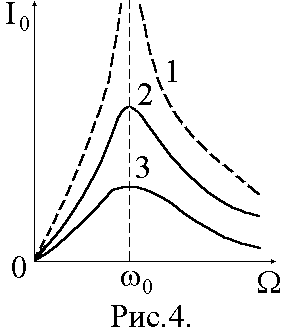 I0 I0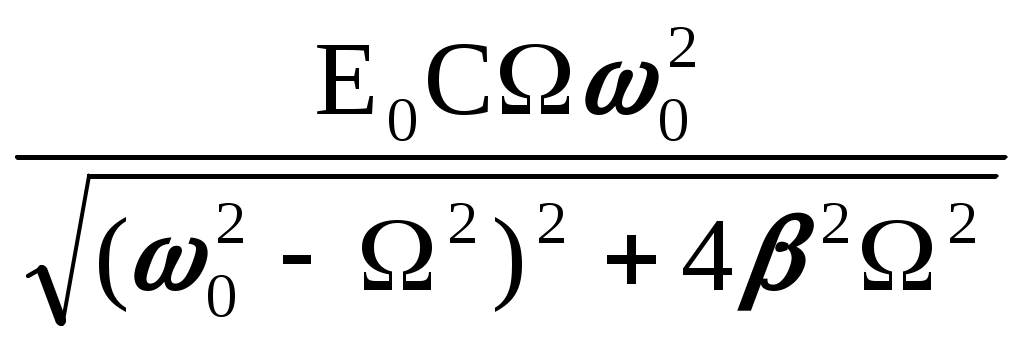 . (15) . (15)Зависимость разности фаз j1 и амплитуды силы тока I0 от частоты W внешнего источника представлена на рис. 4 и 5. Сдвиг фаз j1 между силой тока в контуре и внешней электродвижущей силой при W = w0 равен нулю. При W > w0 сила тока отстает по фазе от напряжения и опережает напряжение, если W < w0. Амплитуда силы тока возрастает при приближении частоты источника электродвижущей силы к собственной частоте контура w0. Это явление называется резонансом в электрической цепи, а кривые (рис. 4) - резонансными кривыми. Величина максимума зависит от b: при b = 0 (R = 0) I0m ® ¥ ( кривая 1); при возрастании b максимальное значение I0m уменьшается (кривые 2 и 3). Острота резонансной кривой связана с добротностью колебательного контура: Q = p¤g = w¤(2b). Найдем ширину DW резонансной кривой на высоте I0m/Ö2 (рис.5). Из формулы (15) следует, что максимальное значение силы тока I0m = E0Сw02/(2b), (15а) I0 = П 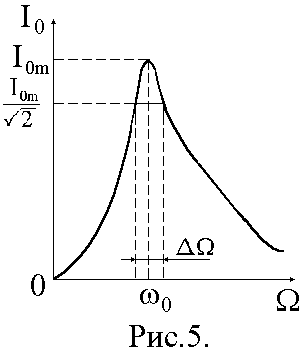 ри I0 = I0m/Ö2 формула (16) перейдет в (17): ри I0 = I0m/Ö2 формула (16) перейдет в (17):Равенство (17) выполняется при 2bW = w02 - W2. Вблизи резонанса можно принять W » w0, w + W » 2w0, а w0 - W = DW/2; следовательно, 2bw0 = (w0 - W)(w0 + W) = (DW¤2)2w0. Отсюда DW¤w0 = 2b¤w0 » 1¤Q, так как при малом затухании b « w0 и w » w0. Относительная ширина резонансной кривой DW¤w0 на высоте I0m/Ö2 при малом затухании равна величине, обратной добротности колебания контура. ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ.Описание установки. Экспериментальная установка представляет собой последовательный колебательный контур (рис.1) с включенным в него амперметром. Роль активного сопротивления играют лампы накаливания различной мощности. Емкость конденсатора и индуктивность катушки также могут варьироваться. Источником переменного тока служит генератор Г3-33. Проведение эксперимента. 1). Включить генератор. Установить по вольтметру генератора напряжение 1 В. 2). Включить установку, предварительно соединив последовательно активное сопротивление, конденсатор и катушку индуктивности. 3). Снять зависимость тока в цепи от частоты переменного тока, меняя частоту генератора с интервалом 5 Гц, начиная с 20 Гц. Результаты измерений занести в таблицу 1. 4). Повторить измерения, меняя активное сопротивление цепи и емкость конденсатора. 5). Результаты измерений занести в таблицы, аналогичные таблице 1.
Обработка результатов эксперимента. 1). Откладывая по оси Х частоту вынуждающей силы W, а по оси Y силу тока I0, построить графики I0(W) для различных значений R при определенных значениях C и L. 2). Построить графики I0(W) для различных значений С при определенных значениях R и L. 3). По графикам определить резонансную частоту w0, ширину резонансной кривой DW и оценить добротность контура Q. 4). По формуле (15а) определить значение величины b и найти индуктивность L. 5). Вычислить относительные погрешности измерений w0 и определить значение величины Q, b и L. Контрольные вопросы1). Дайте определение колебательного контура и расскажите о процессах, происходящих в нем. 2). Что называется добротностью контура? 3). При каких условиях в контуре будут происходить колебания? 4). Дайте определение резонанса и расскажите об условии его наблюдения. 5). При каких значениях активного сопротивления контура резонанс в нем проявляется наиболее ярко? 1 2 |
