Гармонические механические колебания. 2. Механические колебания
 Скачать 1.24 Mb. Скачать 1.24 Mb.
|
|
Содержание
1.Введение: Механические колебания: гармонические, затухающие и вынужденные колебания Колебания называются процессами, которые отличаются различной степенью повторяемости (колебание маятника часов, колебания струны или ножки камертона, напряжение между пластинами конденсатора в радиосвязи, функция сердца). В зависимости от физической природы повторяющегося процесса различаются колебания: механические, электромагнитные, электромеханические и т. Д. Будем рассматривать механические колебания. Колебания, происходящие в отсутствие трения и внешних сил, называются внутренними; их частота зависит только от свойств системы. Простейшими являются гармонические колебания, то есть такие колебания, в которых колеблющаяся величина (например, отклонение маятника) изменяется во времени в соответствии с законом синуса или косинуса. 2.Механические колебания Механические колебания – это физические процессы, точно или приблизительно повторяющиеся через одинаковые интервалы времени. Колебания играют огромную роль в нашей жизни. Примерами колебаний в нашем организме являются биение сердца, движение голосовых связок. Колебания происходят и в жизни нашей планеты (приливы, отливы, землетрясения) и в астрономических явлениях (пульсации звезд). Одним из грозных явлений природы является землетрясение – колебание земной поверхности. Строители рассчитывают возводимые ими сооружения на устойчивость при землетрясении. Без знания законов колебаний нельзя было бы создать, телевидение, радио и многие современные устройства и машины. Неучтенные колебания могут привести к разрушению сложных технических сооружений и вызвать серьезные заболевания человека. Все это делает необходимым их всестороннее изучение. Основным признаком колебательного движения является его периодичность. Колеблющееся тело за одно колебание дважды проходит положение равновесия. Колебания характеризуются такими величинами как период, частота, амплитуда и фаза колебаний. Амплитуда – это наибольшее смещение колеблющейся величины от положения равновесия. При малых амплитудах путь пройденный телом за одно полное колебание равен примерно четырем амплитудам. Промежуток времени, в течение которого тело совершает одно полное колебание, называют периодом колебаний. Период – это время одного полного колебания. Чтобы найти период колебаний нужно разделить время колебаний на число колебаний. [T] = 1с Частота колебаний – это число колебаний за единицу времени. [v] = 1 Гц (герц) Единица частоты названа в честь немецкого ученого Г. Герца. Фаза колебаний – это физическая величина определяющая отклонение колеблющейся величины от положения равновесия в данный момент времени. [ω] = 1 рад/ с Во всех колебательных системах действуют силы, стремящиеся вернуть тело в состояние устойчивого равновесия. Существуют несколько типов маятников: нитяные и, пружинные и т.д. Под словом «маятник» понимают твердое тело способное совершать колебания под действием приложенных сил около неподвижной точки или вокруг оси. Мы с вами будем рассматривать пружинный и математический маятники. 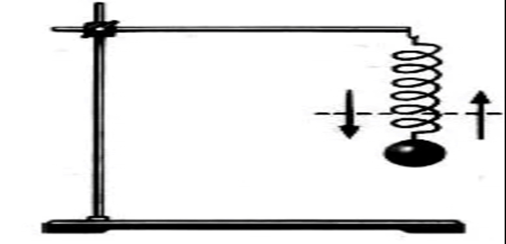 Пружинный маятник. Колебательная система в этом случае представляет собой тело, прикрепленное к пружине. Колебания в таком маятнике возникают под действием силы упругости пружины и силы тяжести. Период колебаний пружинного маятника: 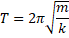 T- период колебаний пружинного маятника m – масса подвешенного груза 𝑘 – жесткость пружины Математический маятник. Математический маятник – это материальная точка, подвешенная на длинной нерастяжимой нити. 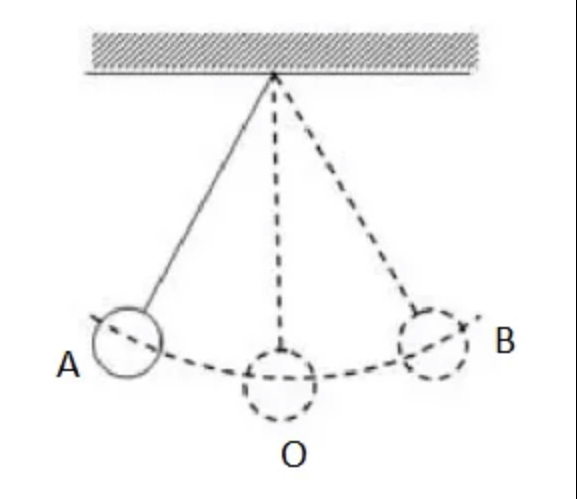 Математический маятник - это идеализированная модель. Реальный маятник можно считать математическим, если длина нити много больше размеров подвешенного тела и масса нити ничтожна по сравнению с массой тела. Колебания такого маятника происходят под действием силы натяжения нити и силы тяжести. Формула для расчета периода колебаний математического маятника была выведена Гюйгенсом. 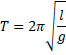 T – период колебаний математического маятника 𝑙 – длина нити маятника 𝑔 – ускорение свободного падения Гюйгенс доказал, что период малых колебаний маятника не зависят от времени. Используя это свойство, названное изохронностью маятника Гюйгенс в тысяча шестьсот пятьдесят седьмом году, сконструировал первые маятниковые часы. Это свойство маятника было открыто 19-летним Галилеем более чем за 20 лет до открытия Гюйгенса. Наблюдая за тем, как раскачиваются в соборе светильники, подвешенные на нитях одинаковой длины, он заметил, что их период колебаний не зависит от времени. Наручных часов тогда не было, и юный Галилей пришёл к решению, которое для многих поколений будет служить образцом блеска и остроумия человеческой мысли: он сравнил колебания маятника с частотой биения собственного сердца. Гармоническими являются колебания, происходящие под действием силы пропорциональной смещению колеблющейся точки и направленной противоположно этому смещению. Уравнение гармонических колебаний: x – координата колеблющейся величины ω - циклическая частота При наличии сил трения в системе колебания затухают. Амплитуда колебаний в этом случае со временем уменьшается. Иногда возникает необходимость в гашении колебаний, к примеру колебания кузова, на рессорах при езде на автомобиле. Для гашения колебаний применяют специальные амортизаторы. С кузовом связывают поршень, который при колебаниях движется в цилиндре, заполненном жидкостью. Большое сопротивление жидкости приводит к гашению колебаний. Колебания, происходящие под действием внешней периодической силы, называются вынужденными. Если частота изменения внешней силы не равна частоте свободных колебаний системы, то внешняя сила будет действовать не в такт со свободными колебаниями самой системы. В этом случае амплитуда колебаний будет определяться максимальным значением действующей на систему внешней силы. Если частота изменения внешней силы совпадет с частотой свободных колебаний, то будет наблюдаться резкое возрастание амплитуды колебаний, так как внешняя сила в этом случае будет действовать в такт со свободными колебаниями этой системы. ω - частота изменения внешней силы. ω0 – частота свободных колебаний системы. Впервые явление резонанса было описано Галилеем. Явление резонанса играет большую роль в природе, технике и науке. Большинство сооружений и машин обладая определенной упругостью, способно совершать свободные колебания. Поэтому внешние периодические воздействия могут вызвать их резонанс, что может стать причиной катастроф. Известно много случаев, когда источником опасных колебаний были люди, идущие в ногу. Так, в 1831 году в городе Манчестер при прохождении по мосту колонны солдат строевым шагом мост разрушился. Аналогичный случай был в г. Петербурге в 1905 году. При прохождении моста через реку Фонтанка эскадроном гвардейской кавалерии мост обрушился. Для предотвращения резонансных явлений используют разные способы гашения вынужденных колебаний. Один способ состоит в изменении частоты свободных колебаний в системе. Другой способ состоит в увеличении силы трения в системе: чем больше сила трения, тем меньше амплитуда резонансных колебаний. 3.Виды колебаний Под колебанием подразумевают процесс, в котором через равные промежутки времени основные характеристики движения имеют одинаковые значения. Периодическими называют такие колебания, при которых значения основных величин повторяются через одинаковые промежутки времени (период колебаний). 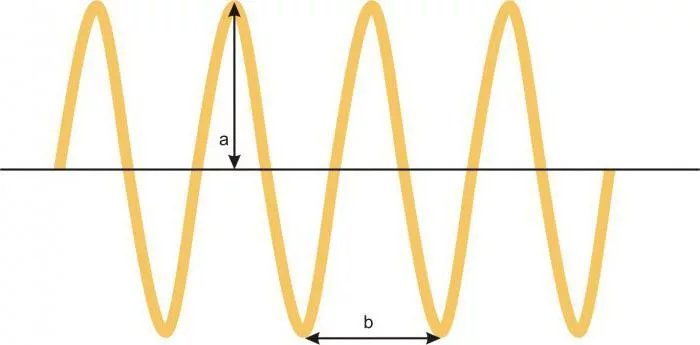 Разновидности колебательных процессов Рассмотрим основные виды колебаний, существующие в фундаментальной физике. Свободными называют колебания, которые возникают в системе, не подвергающейся внешним переменным воздействиям после начального толчка. В качестве примера свободных колебаний является математический маятник. Те виды механических колебаний, которые возникают в системе под действием внешней переменной силы. Особенности классификации По физической природе выделяют следующие виды колебательных движений: механические; тепловые; электромагнитные; смешанные. По варианту взаимодействия с окружающей средой Виды колебаний по взаимодействию с окружающей средой выделяют несколько групп. Вынужденные колебания появляются в системе при действии внешнего периодического действия. В качестве примеров такого вида колебаний можно рассмотреть движение рук, листья на деревьях. Для вынужденных гармонических колебаний возможно появление резонанса, при котором при равных значениях частоты внешнего воздействия и осциллятора при резком возрастании амплитуды. Собственные это колебания в системе под воздействием внутренних сил после того, когда она будет выведена из равновесного состояния. Простейшим вариантом свободных колебаний является движение груза, который подвешен на нити, либо прикреплен к пружине.  Автоколебаниями называют виды, при которых у системы есть определенный запас потенциальной энергии, идущей на совершение колебаний. Отличительной чертой их является тот факт, что амплитуда характеризуется свойствами самой системы, а не первоначальными условиями. Автоколебаниями называют виды, при которых у системы есть определенный запас потенциальной энергии, идущей на совершение колебаний. Отличительной чертой их является тот факт, что амплитуда характеризуется свойствами самой системы, а не первоначальными условиями.Для случайных колебаний внешняя нагрузка имеет случайное значение. Основные параметры колебательных движений. Все виды колебаний имеют определенные характеристики, о которых следует упомянуть отдельно. Амплитудой называют максимальное отклонение от положения равновесия отклонение колеблющейся величины, измеряется она в метрах. Период является время одного полного колебания, через который повторяются характеристики системы, вычисляется в секундах. Частота определяется количеством колебаний за единицу времени, она обратно пропорциональна периоду колебаний. Фаза колебаний характеризует состояние системы.  Характеристика гармонических колебаний Такие виды колебаний происходят по закону косинуса или синуса. Фурье удалось установить, что всякое периодическое колебание можно представить в виде суммы гармонических изменений путем разложения определенной функции в ряд Фурье. В качестве примера можно рассмотреть маятник, имеющий определенный период и циклическую частоту. Чем характеризуются такие виды колебаний? Физика считает математический маятник идеализированной системой, которая состоит из материальной точки, которая подвешена на невесомой нерастяжимой нити, колеблется под воздействием силы тяжести. Такие виды колебаний обладают определенной величиной энергии, они распространены в природе и технике. При продолжительном колебательном движении происходит изменение координаты его центра масс, а при переменном токе меняется значение тока и напряжения в цепи. Выделяют разные виды гармонических колебаний по физической природе: электромагнитные, механические и др. В качестве вынужденных колебаний выступает тряска транспортного средства, которое передвигается по неровной дороге. 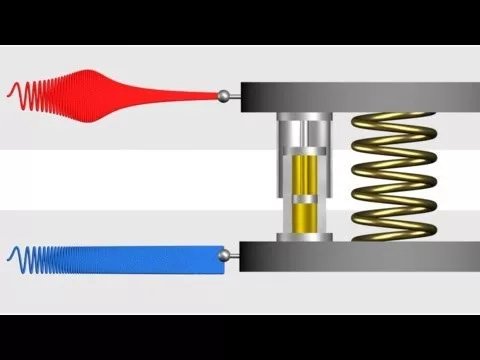 Основные отличия между вынужденными и свободными колебаниями Эти виды электромагнитных колебаний отличаются по физическим характеристикам. Наличие сопротивления среды и силы трения приводят к затуханию свободных колебаний. В случае вынужденных колебаний потери энергии компенсируются ее дополнительным поступлением от внешнего источника. Период пружинного маятника связывает массу тела и жесткость пружины. В случае математического маятника он зависит от длины нити. При известном периоде можно вычислить собственную частоту колебательной системы. В технике и природе существуют колебания с разными значениями частот. К примеру, маятник, который колеблется в Исаакиевском соборе в Петербурге, имеет частоту 0,05 Гц, а у атомов она составляет несколько миллионов мегагерц. Через некоторый промежуток времени наблюдается затухание свободных колебаний. Именно поэтому в реальной практике применяют вынужденные колебания. Они востребованы в разнообразных вибрационных машинах. Вибромолот является ударно-вибрационной машиной, которая предназначается для забивки в грунт труб, свай, иных металлических конструкций. 4.Гармонические колебания Простейшим видом колебаний являются гармонические колебания, которые описываются уравнением x = x m cos ( ω t + φ 0 ) , где x – смещение тела от положения равновесия, x m – амплитуда колебаний, ω – циклическая или круговая частота, t – время. Величина, располагаемая под знаком косинуса, получила название фазы гармонического процесса: φ = ω t + φ 0 . Если t = 0 , φ = φ 0 , тогда φ 0 рассматривается в качестве начальной фазы. Период колебаний Т – это минимальный промежуток времени, через который происходят повторения движения тела. Величина, обратная периоду колебаний, называют частотой колебаний f = 1 T. Частота гармонических колебаний показывает их количество, совершаемое за единицу времени, измеряемая в герцах ( Г ) . Связь с циклической частотой ω и периодом T выражается с помощью формулы: ω = 2 π f = 2 π T . Рисунок 2 . 1 . 2 показывает гармонические колебания тел с разными положениями тел. Данный эксперимент наблюдается в специальных условиях при наличии периодических вспышек освещения, называемого стробоскопическим. Для изображения векторов скорости тела в разные моменты времени используют стрелки. 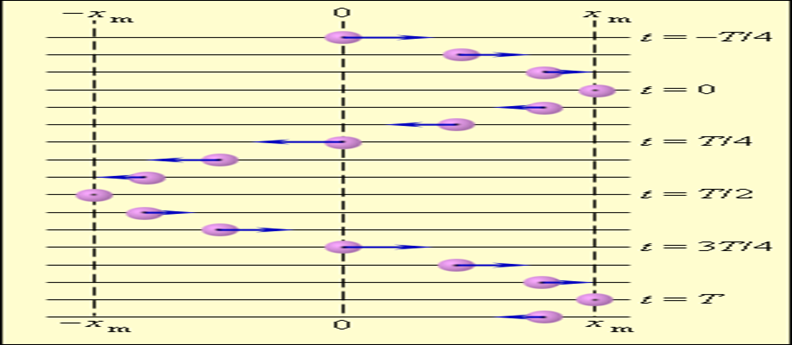 Рис. 2 . 1 . 2 . Стробоскопическое изображение гармонических колебаний. Начальная фаза φ 0 = 0 . Интервал времени между последовательными положениями тела τ = T 12 . На графике 2 . 1 . 3 . показаны изменения, происходящие во время гармонического процесса, при изменении амплитуды колебаний x m , или периода Т (частоты f ), или начальной фазы φ 0 . 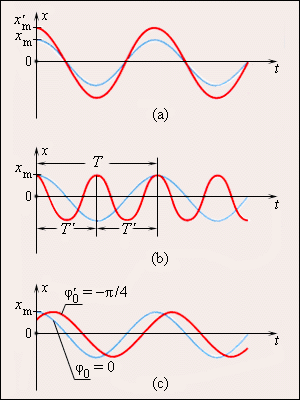 Рис. 2 . 1 . 3 . Во всех трех случаях для синих кривых φ 0 = 0 : a – красная кривая отличается от синей только большей амплитудой ( x ' m > x m ) ; b – красная кривая отличается от синей только значением периода ( T ' = T 2 ) ; с – красная кривая отличается от синей только значением начальной фазы ( φ ′ 0 = − π 2 р а д ) . Гармонический закон. Если колебания совершаются вдоль прямой О х , тогда направление вектора скорости аналогично. Определение скорости движения тела υ = υ x определяют из выражения υ = Δ x Δ t ; ( Δ t → 0 ) . Отношение Δ x Δ t при Δ t → 0 математика трактует как вычисление производной функции x ( t ) за определенное время t . Обозначение принимает вид d x ( t ) d t , x ' ( t ) или ˙ x . Гармонический закон движения записывается в качестве x = x m cos ( ω t + φ 0 ) . После вычисления производной формула приобретает вид: υ = ˙ x ( t ) = − ω x m sin( ω t + φ 0 ) = ω x m cos ( ω t + φ 0 + π 2 ) . Слагаемое + π 2 считают изменением начальной фазы. Достижение максимального значения скорости по модулю υ = ω x m производится при прохождении тела через положение равновесия, то есть ( x = 0 ) . Аналогично определяют ускорение a = a x . Тогда a = Δ υ Δ t , ( Δ t → 0 ) . Отсюда следует, что a равняется производной функции υ ( t ) за время t или второй производной функции x ( t ) . Подставив выражения, получим a = ˙ υ ( t ) = ¨ x ( t ) = − ω 2 x m cos ( ω t + φ 0 ) = − ω 2 x ( t ) . Наличие отрицательного знака указывает на то, что ускорение a ( t ) имеет противоположный смещению x ( t ) знак. Исходя из второго закона Ньютона, сила, которая заставляет совершать колебательные движения, направляется в сторону положения равновесия ( x = 0 ) .  На рисунке 2 . 1 . 4 изображены графики, где имеются зависимости скорости, ускорения, совершающие гармонические колебания. Рис.2 . 1 . 4 . Графики координаты x ( t ) , скорости υ ( t ) и ускорения a ( t ) тела, совершающего гармонические колебания. 5.Свободные колебания, уравнения свободных незатухающих и затухающих колебаний Свободными или собственными называются такие колебания, которые происходят в системе, предоставленной самой себе, после того как она была выведена из положения равновесия. Примером могут служить колебания шарика, подвешенного на нити. Для того чтобы вызвать колебания, нужно либо толкнуть шарик, либо, отведя в сторону, отпустить его. При толчке шарику сообщается кинетическая энергия, а при отклонении - потенциальная. Свободные колебания совершаются за счет первоначального запаса энергии. Свободные незатухающие колебания Свободные колебания могут быть незатухающими только при отсутствии силы трения. В противном случае первоначальный запас энергии будет расходоваться на ее преодоление, и размах колебаний будет уменьшаться. В качестве примера рассмотрим колебания тела, подвешенного на невесомой пружине, возникающие после того, как тело отклонили вниз, а затем отпустили (рис. 1.2).
 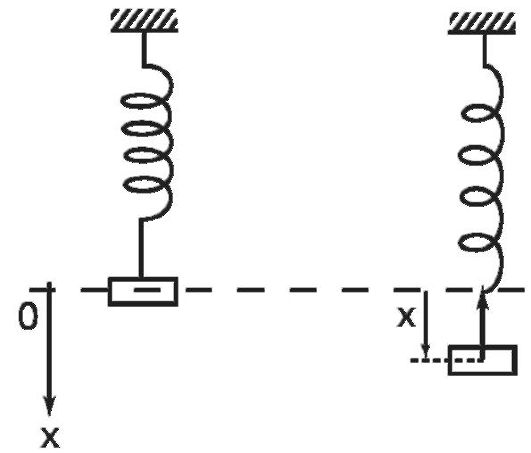 Рис. 1.2. Колебания тела на пружине  Постоянный множитель k называется жесткостью пружины и зависит от ее размеров и материала. Знак «-» указывает, что сила упругости всегда направлена в сторону, противоположную направлению смещения, т.е. к положению равновесия. Постоянный множитель k называется жесткостью пружины и зависит от ее размеров и материала. Знак «-» указывает, что сила упругости всегда направлена в сторону, противоположную направлению смещения, т.е. к положению равновесия.  После переноса всех слагаемых в левую часть и деления на массу тела (m) получим дифференциальное уравнение свободных колебаний при отсутствии трения: После переноса всех слагаемых в левую часть и деления на массу тела (m) получим дифференциальное уравнение свободных колебаний при отсутствии трения:  Величина ω0 (1.6) оказалась равной циклической частоте. Эту частоту называют собственной. Величина ω0 (1.6) оказалась равной циклической частоте. Эту частоту называют собственной.Таким образом, свободные колебания при отсутствии трения являются гармоническими, если при отклонении от положения равновесия возникает упругая сила (1.4). Собственная круговая частота является основной характеристикой свободных гармонических колебаний. Эта величина зависит только от свойств колебательной системы (в рассматриваемом случае - от массы тела и жесткости пружины). В дальнейшем символ ω0 всегда будет использоваться для обозначения собственной круговой частоты (т.е. частоты, с которой происходили бы колебания при отсутствии силы трения). Амплитуда свободных колебаний определяется свойствами колебательной системы (m, k) и энергией, сообщенной ей в начальный момент времени. При отсутствии трения свободные колебания, близкие к гармоническим, возникают также и в других системах: математический и физический маятники (теория этих вопросов не рассматривается) (рис. 1.3). Математический маятник - небольшое тело (материальная точка), подвешенное на невесомой нити (рис. 1.3 а). Если нить отклонить от положения равновесия на небольшой (до 5°) угол α и отпустить, то тело будет совершать колебания с периодом, определяемым по формуле где L - длина нити, g - ускорение свободного падения.  Рис. 1.3. Математический маятник (а), физический маятник (б) Рис. 1.3. Математический маятник (а), физический маятник (б)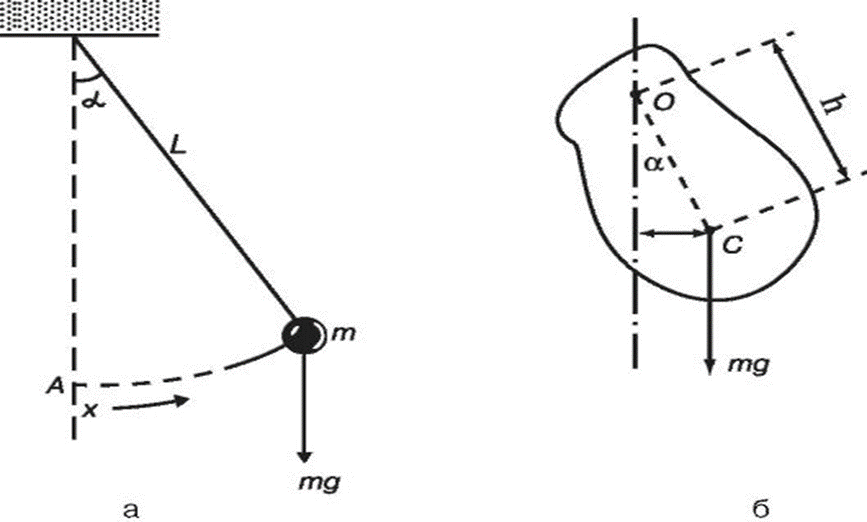  Физический маятник - твердое тело, совершающее колебания под действием силы тяжести вокруг неподвижной горизонтальной оси. На рисунке 1.3 б схематически изображен физический маятник в виде тела произвольной формы, отклоненного от положения равновесия на угол α. Период колебаний физического маятника описывается формулой Физический маятник - твердое тело, совершающее колебания под действием силы тяжести вокруг неподвижной горизонтальной оси. На рисунке 1.3 б схематически изображен физический маятник в виде тела произвольной формы, отклоненного от положения равновесия на угол α. Период колебаний физического маятника описывается формулой  где J - момент инерции тела относительно оси, m - масса, h - расстояние между центром тяжести (точка С) и осью подвеса (точка О). где J - момент инерции тела относительно оси, m - масса, h - расстояние между центром тяжести (точка С) и осью подвеса (точка О).Момент инерции - это величина, зависящая от массы тела, его размеров и положения относительно оси вращения. Вычисляется момент инерции по специальным формулам. Свободные затухающие колебания Силы трения, действующие в реальных системах, существенно изменяют характер движения: энергия колебательной системы постоянно убывает, и колебания либо затухают, либо вообще не возникают. Сила сопротивления направлена в сторону, противоположную движению тела, и при не очень больших скоростях пропорциональна величине скорости:  График таких колебаний представлен на рис. 1.4. В  качестве характеристики степени затухания используют безразмерную величину, называемую логарифмическим декрементом затухания λ.  Рис. 1.4. Зависимость смещения от времени при затухающих колебаниях Рис. 1.4. Зависимость смещения от времени при затухающих колебаниях где i - порядковый номер колебания. где i - порядковый номер колебания.Нетрудно видеть, что логарифмический декремент затухания находится по формуле  Сильное затухание. При выполнении условия β ≥ ω0 система возвращается в положение равновесия, не совершая колебаний. Такое движение называется апериодическим. На рисунке 1.5 показаны два возможных способа возвращения в положение равновесия при апериодическом движении. Сильное затухание. При выполнении условия β ≥ ω0 система возвращается в положение равновесия, не совершая колебаний. Такое движение называется апериодическим. На рисунке 1.5 показаны два возможных способа возвращения в положение равновесия при апериодическом движении.
 Рис. 1.5. Апериодическое движение Рис. 1.5. Апериодическое движение6.Колебания груза на пружине, математический маятник Второй закон Ньютона (основной закон динамики): ускорение, приобретаемое материальной точкой, прямо пропорционально равнодействующей всех сил, действующих на нее, и обратно пропорционально массе материальной точки: 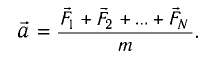 Закон Гука: модуль силы упругости  , возникающей в теле при упругих деформациях, прямо пропорционален его абсолютному удлинению (сжатию) , возникающей в теле при упругих деформациях, прямо пропорционален его абсолютному удлинению (сжатию)  где k — жесткость тела, Рассмотрим пружинный маятник, представляющий собой колебательную систему, образованную грузом на пружине. Пусть груз массой т, лежащий на гладкой горизонтальной поверхности, прикреплен к свободному концу невесомой пружины жесткостью k (рис. 3). Второй конец пружины закреплен относительно данной инерциальной системы отсчета (ИСО). 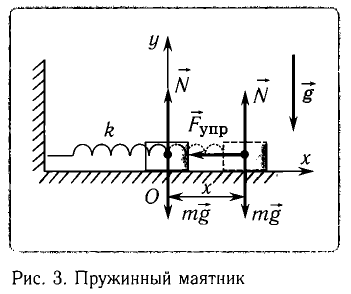 Выведем груз из положения равновесия, сместив его на расстояние х вправо. В пружине возникнет сила упругости  направленная влево. направленная влево.Запишем второй закон Ньютона для движения груза: 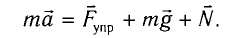 В проекции на ось Ох действующих на груз сил с учетом закона Гука получаем 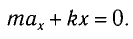 Следовательно, 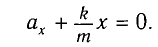 Это уравнение аналогично уравнению гармонических колебаний 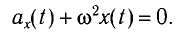 Сравнивая эти два уравнения, находим циклическую частоту колебаний пружинного маятника: 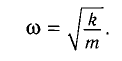 Тогда период колебаний пружинного маятника можно найти по формуле 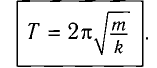 Как следует из полученной формулы, период колебаний пружинного маятника не зависит от амплитуды его колебаний (в пределах выполнимости закона Гука). Свойство независимости периода колебаний маятника от амплитуды называется изохронностью (от греческих слов Изохронность колебаний маятника была открыта Галилео Галилеем в 1583 г. при изучении движения грузика, подвешенного на нити. Моделью данной колебательной системы является математический маятник. Математическим маятникомназывается материальная точка массой т, подвешенная на невесомой нерастяжимой нити длиной l в поле каких-либо сил, например силы тяжести Земли (рис. 4). 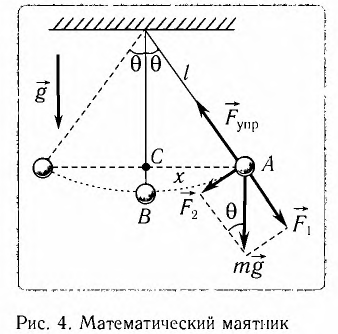 Математический маятник — это идеализированная модель реального маятника при условии, что длина нити намного больше размеров подвешенного на ней тела и масса нити намного меньше массы тела. Кроме того, деформацией нити можно пренебречь. Галилео Галилей экспериментально определил, что период малых колебаний (9 < 10°) математического маятника в поле силы тяжести не зависит от его массы и амплитуды колебаний (угла начального отклонения Период малых колебаний математического маятника в поле силы тяжести Земли определяется по формуле Гюйгенса: 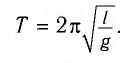 При углах отклонения математического маятника Отклонение маятника от положения равновесия будем характеризовать углом Согласно второму закону Ньютона для движения шарика можем записать: 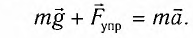 Смещение маятника вдоль дуги х = l 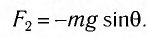 Заметим, что при малых углах  очень мало отличается от длины хорды очень мало отличается от длины хорды 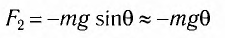 (1) (1)является очень хорошим приближением. Подставляя в выражение (1) значение 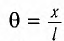 , получим , получим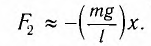 Таким образом, уравнение движения маятника запишется в виде 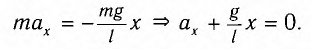 Поскольку полученное уравнение совпадает с уравнением гармонических колебаний  Как видно из этой формулы, циклическая частота не зависит от массы маятника и амплитуды его колебаний, а определяется только его длиной и ускорением свободного падения. В общем случае, когда маятник находится в однородных полях нескольких сил, для определения периода колебаний следует ввести «эффективное ускорение» 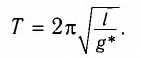 7. Сложение гармонических колебаний, биения, фигуры Лиссажу Сложение одинаково направленных колебаний можно производить методом векторных диаграмм. Любое гармоническое колебание можно представить в виде вектора следующим образом. Выберем ось хс началом отсчета в точке О (рис.1.1.7) Из точки О построим вектор то есть она совершает гармонические колебания с амплитудой а. Р 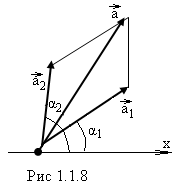 ассмотрим два гармонических колебания одинакового направления и одинаковой циклической малой ассмотрим два гармонических колебания одинакового направления и одинаковой циклической малойрезультирующий вектор Проведем сложение взаимно перпендикулярных колебаний. Пусть материальная точка совершает два взаимно перпендикулярных колебания частотой 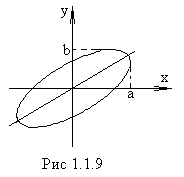 . .Сама материальная точка при этом будет двигаться по некоторой криволинейной траектории. Из уравнения движения следует:  , ,т 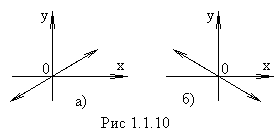 огда огда . (1.1.9) . (1.1.9)Из уравнения (1.1.9) можно получить уравнение эллипса (рис.1.1.9): 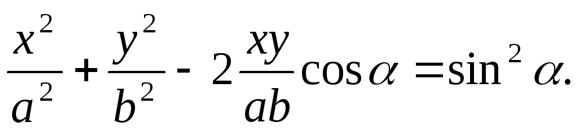  Рассмотрим частные случаи этого уравнения: 1. 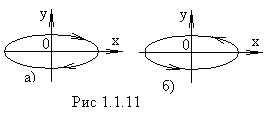 Разность фаз колебанийα= 0. При этом Разность фаз колебанийα= 0. При этом 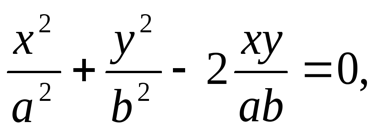 т.е. т.е. 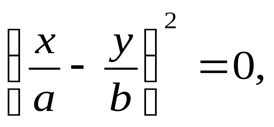 или или 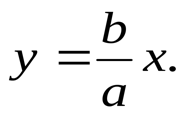 Это уравнение прямой, и результирующее колебание происходит вдоль этой прямой с амплитудой Это уравнение прямой, и результирующее колебание происходит вдоль этой прямой с амплитудой 2. Если разность фаз 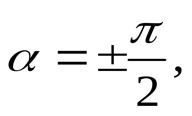 то уравнение (1.1.9) переходит в уравнение эллипса, приведенного к координатным осям, то уравнение (1.1.9) переходит в уравнение эллипса, приведенного к координатным осям, 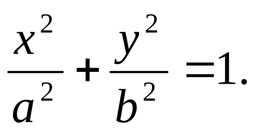 При При 3. Если частоты колебаний неодинаковы, то материальная точка описывает фигуры Лиссажу (рис.1112). Рассмотрим сложение колебаний одного направления, частоты которых мало отличаются друг от друга. В этом случае результирующее движение можно рассматривать как гармоническое колебание с пульсирующей амплитудой. Такие колебания называются биениями. Пусть частота одного колебания 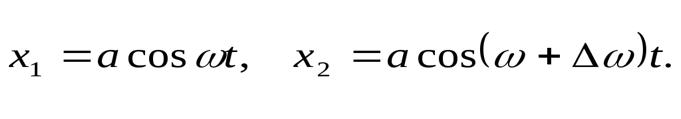 С 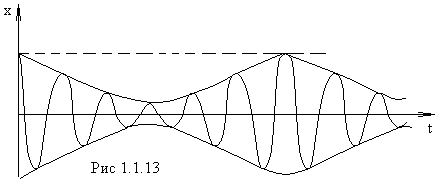 ложим эти выражения: ложим эти выражения: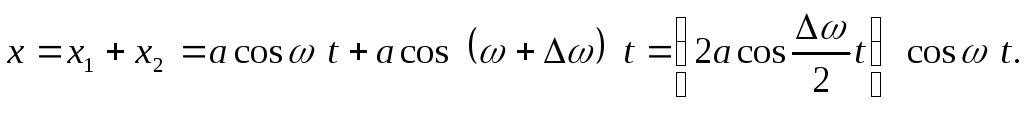 (1.1.10) (1.1.10)Множитель 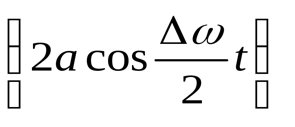 меняется гораздо медленнее, чем меняется гораздо медленнее, чем 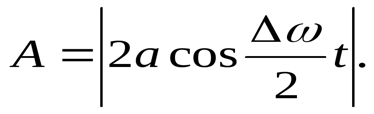 Частота изменения амплитуды – частота биений – равна разности частот складываемых колебаний 8.Заключение Колебания играют огромную роль в жизни человека. Без знания законов колебаний нельзя было бы создать радио, телевидение, многие современные устройства и машины. Колебания многогранны. Иногда они выступают как друг и помощник человека, а иногда как коварный враг. Неучтенные колебания могут привести к разрушению сложных технических сооружений и вызвать серьезные заболевания человека. 9.Список используемой литературы 1. Элементарный учебник физики под редакцией академика Г. С. Ландсберга. Том III. Колебания и волны. Оптика. Атомная и ядерная физика. - 10-е изд., перераб. - М.: Наука. Главная редакция физико-математический литературы, 1986. 2. Кикоин И. К., Кикоин А. К. Физика: учебник для 9 кл. сред. шк. - М.: Просвещение, 1990. 3. Шахмаев Н. М. и др. Физика: учеб. Для 9 кл. сред. шк. - 3-е изд. - М.: Просвещение, 1994. 4. Эрик Рождерс. Физика для любознательных. Том I. Материя, движение, сила. - 2-е изд., исправл. - М.: Мир, 1972. 5. Интернет-ресурсы. 6. Тарасов Л. В. Современный курс физики. Механика. - М.: ООО «Издательство Оникс»: ООО «Издательство «Мир и образование», 2009. |

