Вариант 3 Задача
 Скачать 37.17 Kb. Скачать 37.17 Kb.
|
|
Вариант 3 Задача: Провести моделирование свободного падения тела с заданными массой и формой в трех различных вязких средах. Скорость движения должна быть столь невелика, чтобы квадратичной составляющей силы сопротивления можно было пренебречь. Изучить влияние вязкости среды на характер движения. Решение: 1. Постановка задачи моделирования Началу моделирования предшествует постановка содержательной задачи моделирования, т.е. переход от когнитивной модели к формулировке в словесной форме основных вопросов об объекте моделирования. Правильная постановка задачи очень важна, так как ошибка на этом этапе потребует вернуться к построению модели с самого начала. Содержательная постановка задачи, называемая в технических дисциплинах техническим заданием, в дальнейшем уточняется и конкретизируется, однако принципиальные, основные положения остаются неизменными. Рассмотрим постановку задачи моделирования, которая позволит описать движение тела в трех различных вязких средах. Сформулируем требования к модели и исходные данные для моделирования. Модель должна позволять вычислять положение тела в трех различных вязких средах в любой момент времени. Исходными данными моделирования являются масса тела, начальные координаты, начальная скорость, плотность (вязкость) среды и объем тела. 2. Концептуальная формулировка задачи На основе содержательной модели, описанной в разделе 1, разрабатывается концептуальная формулировка задачи моделирования. Применительно к рассматриваемой задачи движение тела может быть описано в соответствии с законами классической механики Ньютона. При построении математической модели, которое будет проводиться на следующем этапе моделирования, примем следующие гипотезы: тело будем считать материальной точной массой m и радиусом r, положение которой совпадает с центром масс тела; скорость движения столь невелика, что квадратичной составляющей силой сопротивления можно пренебречь. движение тела происходит в гравитационном поле Земли в соответствии с законами классической механики Ньютона. никакие силы, кроме вертикальных, на предмет не действуют; для удобства вычислений будем предполагать, что тело имеет форму шара. 3. Построение математической модели Перейдем к составлению математической модели объекта - совокупности математических соотношений, которые описывают его поведение и свойства. Уравнения, образующие математическую модель, формируются на основании законов и определяющих выражений предметной области. Математическая модель движения тела будет являться моделью тела, совершающего свободное падение, и окончательный вид этой модели представляет собой систему дифференциальных уравнений. На шарик, падающий в вязкой среде, по вертикали действуют три силы,: Сила тяжести (тяготения) 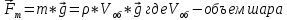 Сила гидростатического выталкивания (сила Архимеда): 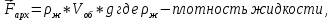 Сила сопротивления среды: 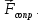 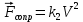 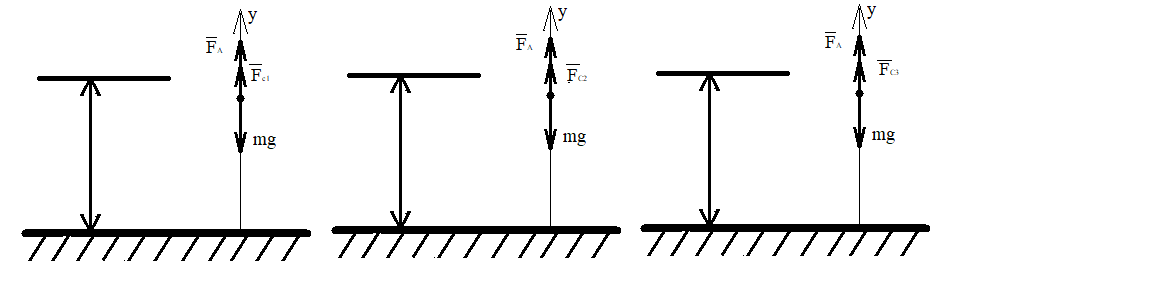 Рисунок 1 Из уравнения Ньютона m 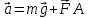 + +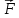 c cПроектируем данное векторное уравнение на ось Y 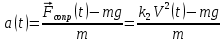 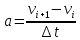 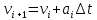 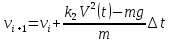  Определим 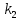 для конкретных ситуаций для конкретных ситуаций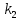 пропорциональна площади поперечного сечения тела пропорциональна площади поперечного сечения тела 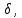 плотности среды плотности среды 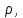 и зависит от формы тела и зависит от формы тела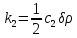 Для шара 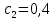 Для диска 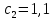 Для полусферы 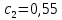 Учитывая действие трех сил, система дифференциальных уравнений будет иметь вид: 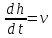 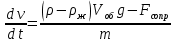 Поскольку при разработке концептуальной модели, раздел 2, мы договорились не учитывать квадратичную составляющую силы сопротивления воздуха, то величина силы сопротивления пропорциональна скорости и имеет место соотношение 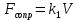 , где , где 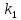 определяется свойствами среды и формой тела. Например, для шара определяется свойствами среды и формой тела. Например, для шара 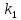 = 6πμr - это формула Стокса, где r - радиус шара, μ - коэффициент вязкости среды, в которой будет двигаться тело. = 6πμr - это формула Стокса, где r - радиус шара, μ - коэффициент вязкости среды, в которой будет двигаться тело. Согласно условию задачи, мы должны изучить падение тела в трех различных средах, тогда переменная μ будет иметь разное значение для каждого случая. Окончательный вид системы дифференциальных уравнений: 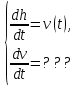 Для обеспечения единственности решения системы дифференциальных уравнений необходимо определить начальное положение тела в пространстве и начальное значение скорости. … (задание начальных значений обосновать) 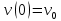 =0 =0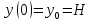 Таким образом, систему дифференциальных уравнений будем рассматривать с начальными условиями: H = ?? м; v0 = ?? м\c; r = ?? м; m = ??кг; μ1 = ?? мПа*с - коэффициент вязкости ??; μ2 = ?? мПа*с - коэффициент вязкости ??; μ3 = ?? мПа*с - коэффициент вязкости ??; Вполне естественно, что этими значениями можно варьировать с целью выполнения нескольких экспериментов при различных начальных данных. Эта особенность обязательно будет отражена при построении имитационной модели. |
