Математика. Решение Найдем уравнение изоклин. По определению уравнение имеет вид f(x,y)k, где kconst
 Скачать 182.63 Kb.
|
ВЫПОЛНЕНИЕ ПРАКТИЧЕСКИХ ЗАДАНИЙ ПО ДИСЦИПЛИНЕ Математика Группа Ал21М511в Студент Ерасыл Нуржанулы Мырзалиев МОСКВА 2022 1.Методом изоклин построить интегральные кривые уравнения. dy/dx=2x(1-y);Решение: Найдем уравнение изоклин. По определению уравнение имеет вид f(x,y)=k, где k=const. Следовательно k=2x(1-y)⇔1-y=k/2x⇔y=1-k/2x. Изоклины представляют собой семейство гипербол. При k=0 имеем y=1 и tgα=k⇔tgα=0⇔α=0° При k=1 имеем y=1-1/2x и tgα=1⇔α=45° При k=-1 имеем y=1+1/2x и tgα=-1⇔α=135° При k=2 имеем y=1-1/x и tgα=1⇔α≈63° При k=-2 имеем y=1+1/x и tgα=-1⇔α≈117° 2. Решить уравнение, допускающее понижения порядка. x2y”=y’2; Решение: В это уравнение второго порядка явно не входит неизвестная функция, следовательно полагая y’=z(x), y”=z’, получим дифференциальное уравнение первого порядка: x2z’=z” dz/z”= dz/x2 1/z= 1/x+ c y’=z=x/1+cx dy=1cx/ c1+cz dx = 1/c*(1+cx/1+cx)*dx- (1/1+cx)dx) y=x/c- ln(1+cx) / c2 + c^ 2)F(y, y’, y”, …, y^n)=0 p(y)=y’ y”=pp’, т.к. y”= dy’/ dx = dp/dy * dy/dx= p’p: 3.Решить систему уравнений: {dx/dt=t/y {dy/dt=-(t/x) Имеем 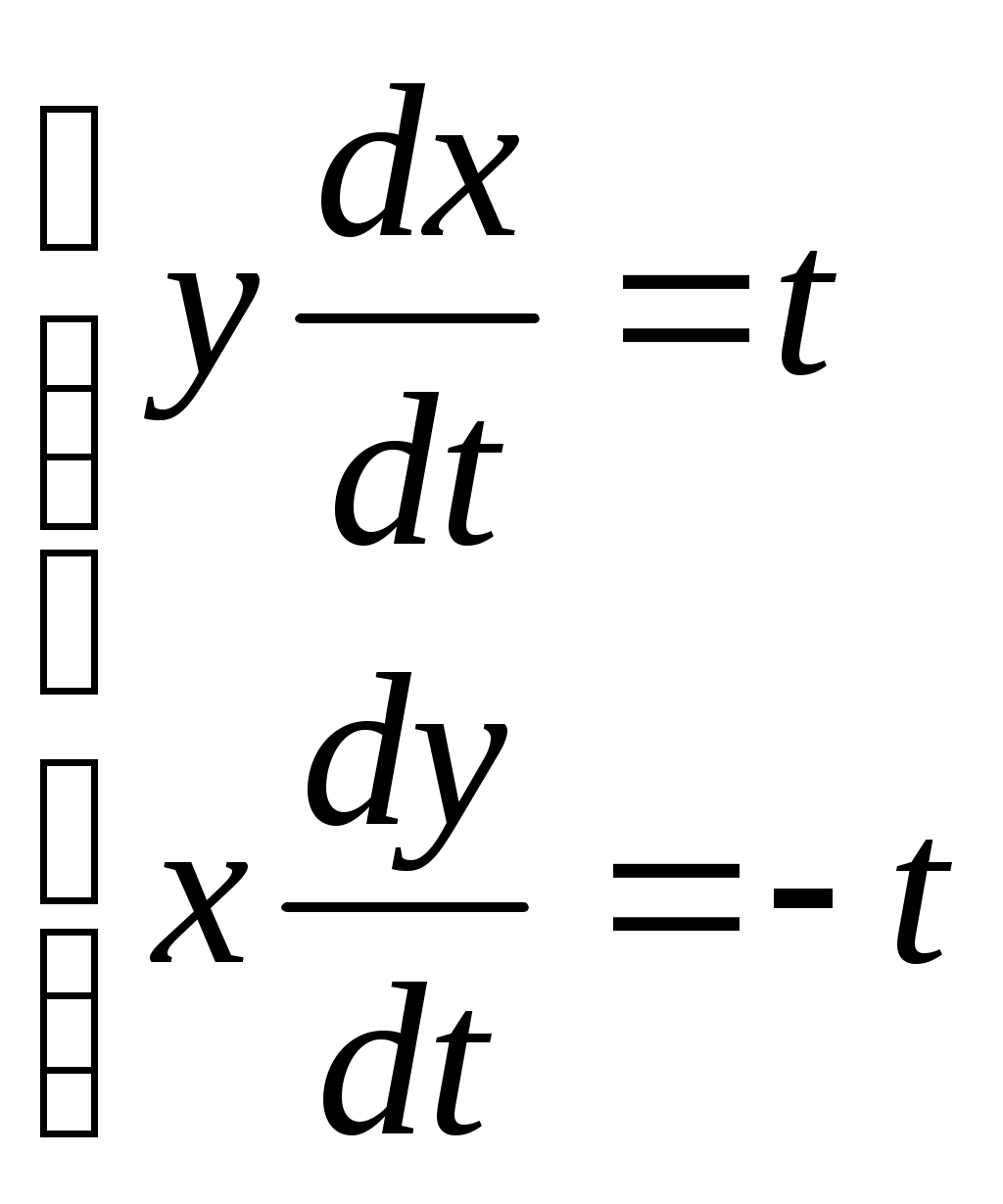 , складываем оба уравнения:  . или  .Следовательно,  . Делаем 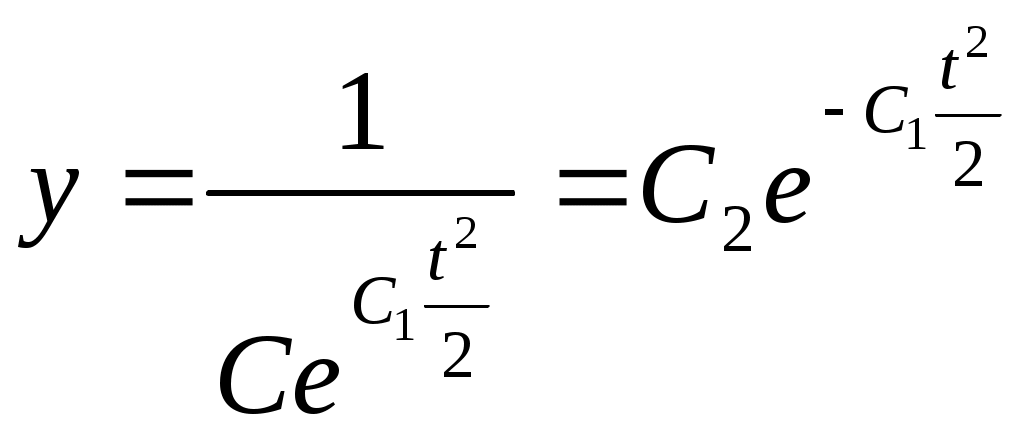подстановку  в первое уравнение системы. или    .Найдем  :  .В итоге: 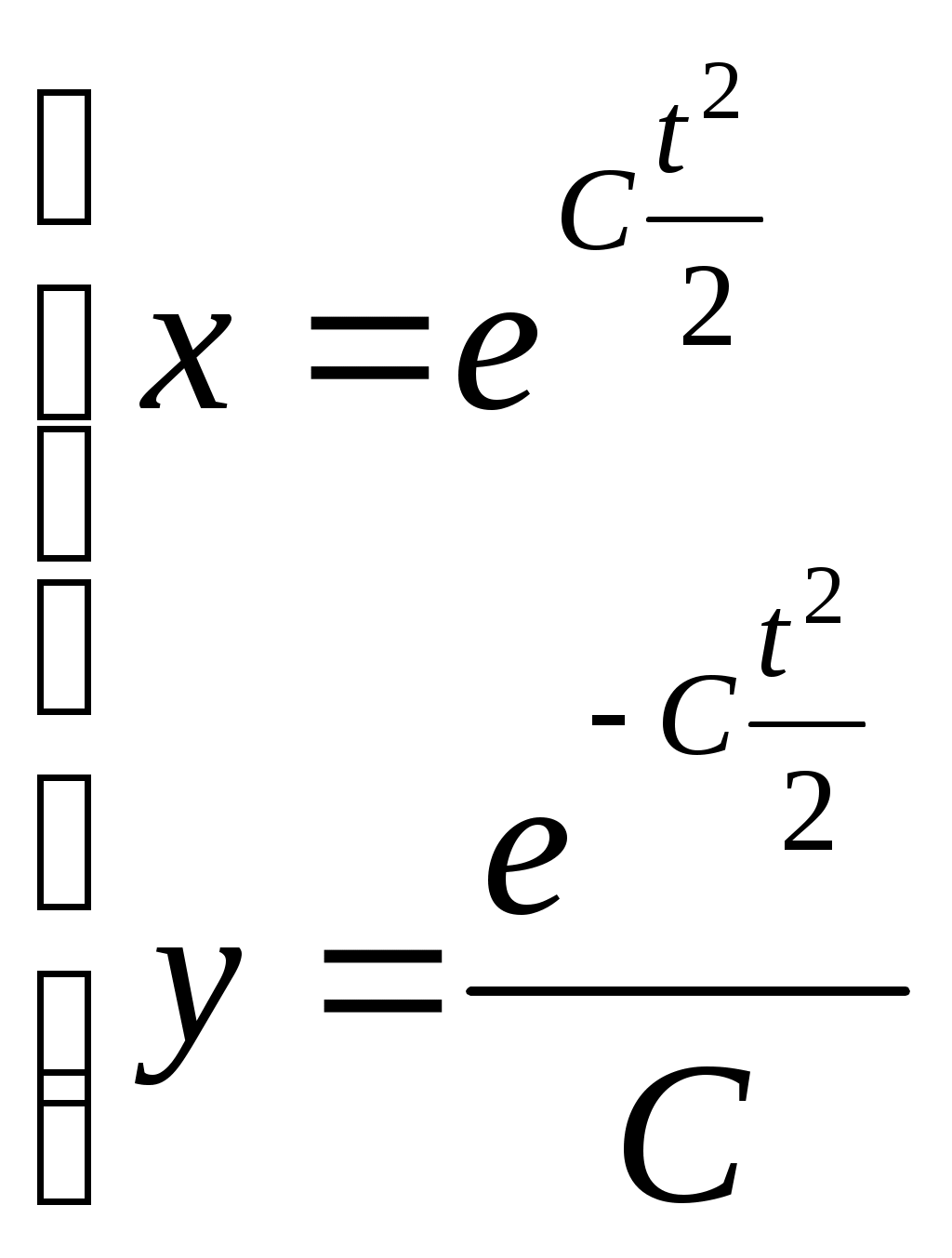 ,  - некоторые постоянные.Ответ: 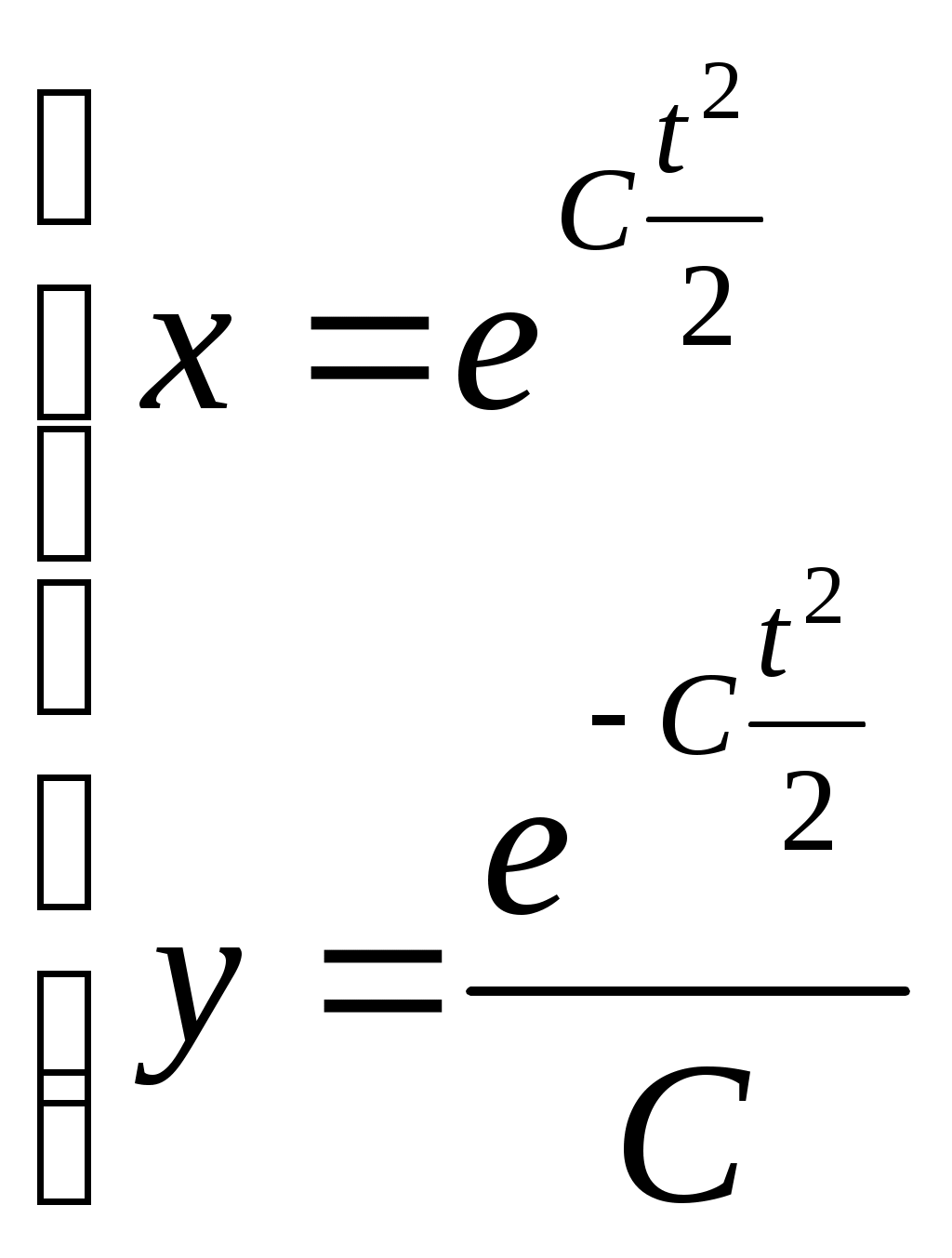.4. Вероятность появления события в каждом испытании равна 0,7. Сколько нужно провести испытаний, чтобы наивероятнейшее число появлений события равнялось 10? Наивероятнейшее число определяется двойным неравенством:  В нашем случае:   Из первого неравенства:  Из второго неравенства:   Так как  – целое число, получаем,  Необходимо провести 14 испытаний. 14 испытаний. Ответ: 14 испытаний; |